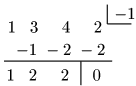高校数学[総目次]
数学Ⅱ 第2章 複素数と方程式
| スライド | ノート | 演習 | |
| 1. 複素数 | |||
| 2. 2次方程式の解と判別式 | |||
| 3. 解と係数の関係 | |||
| 4. 剰余の定理・因数定理 | |||
| 5. 高次方程式 |

5.高次方程式
5.1 高次方程式の解法
多項式 $P(x)$ が3次以上のとき,方程式 $P(x)=0$ を高次方程式という.
例題 $x^3+3x^2+4x+2=0$ を解け.
解法の手順
①発見的に1つ解 ($\alpha$ とする) を見つける
↓
②$P(x)$ を $x-\alpha$ で割る
↓
③商が2次式になるまで①,②を繰り返す
こたえ
手順① 発見的に解の1つを見つける
係数が整数,かつ最高次の係数が1
→ 解の候補は定数項の正負の約数(前節
)
→ $\pm1,\ \pm2$ このうち $-1$ が解.


手順③ 手順①,②を全ての因数が2次以下になるまで繰り返す.
よって,$(x+1)(x^2+2x+2)=0$ より
\[\underline{\boldsymbol{x=-1,\ -1\pm i}}\]

5.2 3次方程式の解と係数の関係
3次方程式 $ax^3+bx^2+cx+d=0$ の3つの解を,$\alpha,\beta,\gamma$ とすると,