高校数学[総目次]
数学Ⅲ 第5章 2次曲線
| スライド | ノート | 問題 | |
| 1. 放物線 | |||
| 2. 楕円 | |||
| 3. 双曲線 | |||
| 4. 2次曲線の平行移動 | |||
| 5. 2次曲線と直線 | |||
| 6. 2次曲線の性質 | |||
| 7. 曲線の媒介変数表示 | |||
| 8. 極座標と極方程式 |

2.楕円
楕円というと,随分と身近な図形であるが,数学的にはどういう図形を楕円と呼ぶのか確認していこう.
2.1 楕円の方程式
楕円とは?
2定点F,F
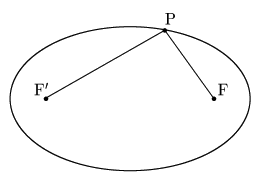
このとき2つの定点F,F
楕円の方程式
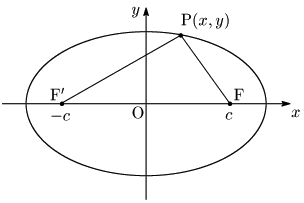
楕円の方程式がどのように表されるのか見ていこう.条件として,
- 焦点:F
- 距離の和:
とする.楕円上の点をPとすると,
両辺を展開して整理すると,
よって,
ここで,
従って条件①を満たす点は,曲線②上にある.逆に曲線②上の任意の点は,
方程式②を,楕円の方程式の標準形という.
楕円の方程式 焦点が F
● 別の求め方
もっとラクに楕円の方程式を求める方法
先の導出法は大抵どの教科書にも採用されている方法であるが,長いルートの式を含んだかなり複雑な計算となっている.実は少しテクニカルだがもっとラクに計算する方法が存在する.スタートは上と同じで
そして次が計算をラクにする重要ポイントである.それは
であるから,左辺を因数分解して
①から
すると,(①
両辺を
発展的補足
楕円上の任意の点から焦点までの距離は,ルートがつかない
平面上の2点
楕円上の任意の点を
と表される.すなわち楕円上の任意の点
これで放物線と楕円の場合について,曲線上の任意の点から焦点までの距離がルートを含まない式として表すことができることを見たが,残る双曲線にも焦点と呼ばれる点があり,この点から双曲線上の点までの距離は,ルートの中身が同じように平方式となって,ルートが外れるのである.この事実は難関大入試問題で,曲線上の2点と焦点を結んだ三角形を考えさせる問題などで活躍する場合がある.

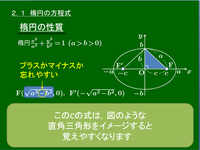
楕円の性質
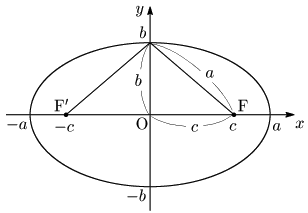
楕円
楕円の性質楕円
- 焦点は
F - 座標軸との交点(頂点)は
- 長軸の長さ
長軸と短軸の交点(楕円の中心) - 楕円上の任意の点から焦点までの距離の和は
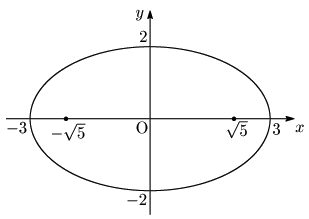
例題 楕円
こたえ

2.2 焦点が
である.これは
- 焦点
- 長軸は

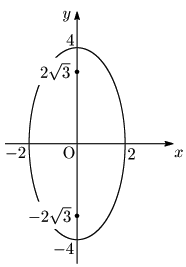
例題 楕円
こたえ
長軸の長さ:

2.3 円と楕円
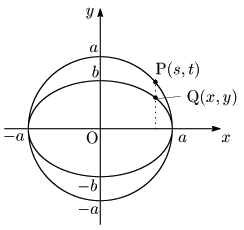
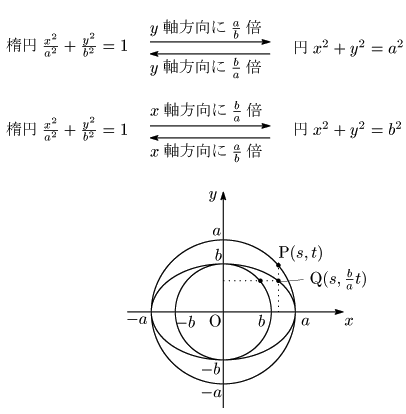
円
これらを①に代入して
よって,点Qの軌跡は,楕円

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第5章 2次曲線
| スライド | ノート | 問題 | |
| 1. 放物線 | |||
| 2. 楕円 | |||
| 3. 双曲線 | |||
| 4. 2次曲線の平行移動 | |||
| 5. 2次曲線と直線 | |||
| 6. 2次曲線の性質 | |||
| 7. 曲線の媒介変数表示 | |||
| 8. 極座標と極方程式 |