高校数学[総目次]
数学Ⅲ 第5章 2次曲線
| スライド | ノート | 問題 | |
| 1. 放物線 | |||
| 2. 楕円 | |||
| 3. 双曲線 | |||
| 4. 2次曲線の平行移動 | |||
| 5. 2次曲線と直線 | |||
| 6. 2次曲線の性質 | |||
| 7. 曲線の媒介変数表示 | |||
| 8. 極座標と極方程式 |

1.放物線
数学Ⅰでは関数 $y=ax^2+bx+c$ のグラフを放物線といったが,ここでは2次曲線という枠組みの中で新たに定義し直す.
1.1 放物線の方程式
2次曲線という枠組みの中での放物線とは
放物線とは?
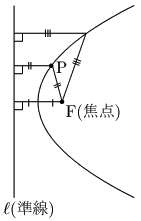
定点Fと,Fを通らない定直線$\ell$からの距離が等しい点Pの軌跡.
定点Fを焦点といい,定直線$\ell$を準線という.
補足
放物線が横を向いているのは何故か
放物線が横を向いたようになっていて違和感があるかもしれない.このあと続く楕円(及び円),双曲線とあわせて2次曲線というが,これらは「定点と定直線からの距離の比が一定である点の軌跡」という形で統一した表現がとれる.この定直線を縦に伸びる直線としたために,放物線がしわ寄せを受けたというわけである.詳しくは 6節 2次曲線の性質 参照

焦点$(p,0)$,準線$x=-p$ の放物線
放物線の定義から方程式を導出する
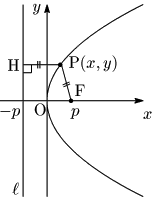
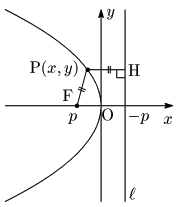
図において,
\[\begin{align*}
{\rm PF}&={\rm PH}\ \ \cdots\ \mbox{①}\\[5pt]
{\rm PF}^2&={\rm PH}^2\\[5pt]
(x-p)^2+y^2&=|x-(-p)|^2\\[5pt]
\therefore y^2&=4px\ \ \cdots\ \mbox{②}
\end{align*}\]
よって条件①を満たす点は,曲線②上にある.逆に曲線②上の任意の点は,上の計算の逆をたどることで条件①を満たす.
方程式②を,放物線の方程式の標準形という.
まとめ $p\neq0$ とする.
焦点 $(p,0)$,準線 $x=-p$ である放物線の方程式は\[y^2=4px\]

