高校数学[総目次]
数学Ⅲ 第5章 2次曲線
| スライド | ノート | 問題 | |
| 1. 放物線 | |||
| 2. 楕円 | |||
| 3. 双曲線 | |||
| 4. 2次曲線の平行移動 | |||
| 5. 2次曲線と直線 | |||
| 6. 2次曲線の性質 | |||
| 7. 曲線の媒介変数表示 | |||
| 8. 極座標と極方程式 |
2．楕円
楕円というと，随分と身近な図形であるが，数学的にはどういう図形を楕円と呼ぶのか確認していこう．
2.1 楕円の方程式
楕円とは？
2定点F，F$’$ からの距離の和が一定である点Pの軌跡を楕円という．
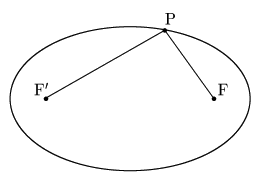
このとき2つの定点F，F$’$ を焦点という．
楕円の方程式
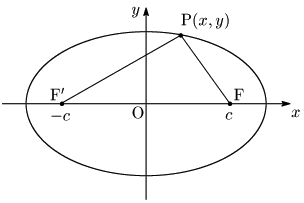
楕円の方程式がどのように表されるのか見ていこう．条件として，
- 焦点：F$(c,0)$，F’$(-c,0)$
- 距離の和：$2a$ (ただし，$a>c>0$)
とする．楕円上の点をPとすると，$\rm{FP+F\,’P}=2a$ である．この式から始めて楕円の方程式を導くまでの途中，2度の平方が行われる．一般に等式を2乗すると同値性が損なわれるが，実は逆も成り立つ．この点について詳しくはスライド で解説する．
\[\begin{align*} &{\rm FP+F\,’P}=2a\ \ \cdots\mbox{①}\\[5pt] \iff &\sqrt{(x-c)^2+y^2}+\sqrt{(x+c)^2+y^2}=2a\\[5pt] \iff &\sqrt{(x-c)^2+y^2}=2a-\sqrt{(x+c)^2+y^2}\\[5pt] \Longrightarrow\ &(x-c)^2+y^2=\left(2a-\sqrt{(x+c)^2+y^2}\right)^2\\[5pt] \end{align*}\]
両辺を展開して整理すると，
\[\begin{align*}
&a\sqrt{(x+c)^2+y^2}=a^2+cx\\[5pt]
\Longrightarrow\ &a^2\{(x+c)^2+y^2\}=(a^2+cx)^2\\[5pt]
\end{align*}\]
よって，
\[(a^2-c^2)x^2+a^2y=a^2(a^2-c^2)\]
ここで，$\sqrt{a^2-c^2}=b$ とおくと，
\[b^2x^2+a^2y^2=a^2b^2\]
$\therefore \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\ \ \cdots$ ②
従って条件①を満たす点は，曲線②上にある．逆に曲線②上の任意の点は，$c=\sqrt{a^2-b^2}$ とおくことで条件①を満たす．(詳しくはスライド で．)
方程式②を，楕円の方程式の標準形という．
楕円の方程式 焦点が F$(c,0)$，F’$(-c,0)$，焦点からの距離の和が $2a$ (ただし，$a>c>0$) である楕円の方程式は，$\sqrt{a^2-c^2}=b$ とおくと
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\]
● 別の求め方
もっとラクに楕円の方程式を求める方法
先の導出法は大抵どの教科書にも採用されている方法であるが，長いルートの式を含んだかなり複雑な計算となっている．実は少しテクニカルだがもっとラクに計算する方法が存在する．スタートは上と同じで
${\rm FP+F\,’P}=2a$ …①
そして次が計算をラクにする重要ポイントである．それは ${\rm FP^2-F\,’P^2}$ を計算するのである．
\[\begin{align*} &{\rm FP^2-F\,’P^2}\\[5pt] =&\{(x-c)^2+y^2\}-\{(x+c)^2+y^2\}\\[5pt] =&-4cx \end{align*}\]
であるから，左辺を因数分解して
\[({\rm FP+F\,’P})({\rm FP-F\,’P})=-4cx\]
①から ${\rm FP+F\,’P}=2a$ であったから，代入して両辺を $2a$ で割ると
${\rm FP-F\,’P}=-\dfrac{2cx}a$ …②
すると，(①$+$②)$\div$2 より，
\[\begin{align*}
{\rm FP}&=a-\frac{cx}a\\[5pt]
\therefore {\rm FP^2}&=\left(a-\frac{cx}a\right)^2\\[5pt]
(x-c)^2+y^2&=a^2-2cx+\frac{c^2}{a^2}x^2\\[5pt]
\frac{a^2-c^2}{a^2}x^2+y^2&=a^2-c^2
\end{align*}\]
$a>c>0$ より，$a^2-c^2>0$ であるから，$b=\sqrt{a^2-c^2}$ とおくと，
\[\frac{b^2}{a^2}x^2+y^2=b^2\]
両辺を $b^2$ で割って
\[\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\]
発展的補足
楕円上の任意の点から焦点までの距離は，ルートがつかない
平面上の2点 $(x_1,\ y_1),\ (x_2,\ y_2)$ の距離は，$\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$ で計算され，通常ルート $\sqrt{\hspace{6mm}}$ は外れないことが多い．ところが 放物線 のときがそうであったように，楕円の場合も楕円上の任意の点と，この楕円の一方の焦点までの距離は，例外的にルートがつかない式として表すことができるのである．