2次曲線の平行移動

高校数学[総目次]

数学Ⅲ　第5章　2次曲線

	スライド	ノート	問題
1. 放物線
2. 楕円
3. 双曲線
4. 2次曲線の平行移動
5. 2次曲線と直線
6. 2次曲線の性質
7. 曲線の媒介変数表示
8. 極座標と極方程式

4．2次曲線の平行移動

4.1 曲線 $F(x,y)=0$ の平行移動

　$F(x,y)=0$ の表す曲線を $x$ 軸方向に $p$，$y$ 軸方向に $q$ だけ平行移動した点の座標を $(X,Y)$ とすると

$\left\{\begin{array}{l} X=x+p\\[5pt] Y=y+q \end{array}\right.$
　
$\therefore \left\{\begin{array}{l} x=X-p\\[5pt] y=Y-q \end{array}\right.$

　これらを $F(x,y)=0$ に代入すると

$F(x-p,y-q)=0$

となる．これが平行移動後の方程式である．

注意

　2次曲線においては，頂点，焦点，準線，漸近線なども同じように平行移動する．

例題　放物線 $y^2=8x$ を，$x$ 軸方向に $-1$, $y$ 軸方向に2だけ平行移動した放物線$C$の方程式，頂点，焦点，準線を求めよ．

こたえ

　解答例を表示する >

　放物線 $C$ の方程式は
$$(y-2)^2=8(x+1)$$
　また，放物線 $y^2=4\cdot2x$ は

頂点 $(0,0)$，焦点 $(2,0)$，準線 $x=-2$

であり，これらも同様に平行移動するから，放物線 $C$ は，

頂点 $(-1,2)$，焦点 $(1,2)$，準線 $x=-3$

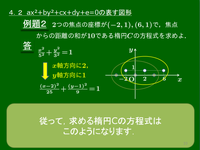
4.2 $ax^2+by^2+cx+dy+e=0$ の表す図形

例題1　$4x^2-9y^2-8x-36y-68=0$ はどのような図形を表すか．