高校数学[総目次]
数学Ⅱ 第2章 複素数と方程式
| スライド | ノート | 演習 | |
| 1. 複素数 | |||
| 2. 2次方程式の解と判別式 | |||
| 3. 解と係数の関係 | |||
| 4. 剰余の定理・因数定理 | |||
| 5. 高次方程式 |

1.複素数
このノートでは,複素数 $a+b\,i$ について,「 $a,\ b$ は実数」という断りを省略することがある.
1.1 複素数
方程式 $x^2=a$ は,$a\geqq0$ のとき $x=\pm\sqrt a$ を解にもつ.例えば $x^2=1$ のとき $x=\pm1$,$x^2=25$ のとき $x=\pm5$,$x^2=0$ のとき $x=0$ 等々.一方,$x^2=-1$ や $x^2=-4$ は解をもたない.どんな数も2乗すると0以上になるからだ.
ここでの目標は,方程式 $x^2=a$ において,$a<0$ の場合であっても解をもつように数を拡張することにある.
2乗すると負になる数を考える
方程式「$x^2=$(負の数)」にも解をもたせるためにはこれまでの数だけでは足りない.次に示す全く新しい数「 $i$ 」を考えることで,この難局を乗り越える.
虚数単位
2乗すると $-1$ になる数を $i$ で表す:
$i^2=-1$
この $i$ を虚数単位(きょすうたんい,$\,i\,\rm{maginay\ unit}$)という.imaginary unit は直訳すれば「想像上の単位」ということになろうが,この「想像」は現実を逃避するためのものではない.歴史上の数学者が編み出したこの $i$ は,遊び心といったおふざけなどでは決してない,数学の骨格を変えるほどの大発明だったのである.$i$ が数学の世界に登場したことで,数学は大いなる進歩を遂げることになる.残念なことに,その素晴らしい内容の大部分は大学で学ぶこととなる.

この虚数単位 $i$ を用いてここに「複素数(ふくそすう)」と呼ばれる新しい数を導入する:
複素数
実数 $a, b$ を用いて,$a+b\,i$ と表される数を複素数 (complex number)という:
複素数
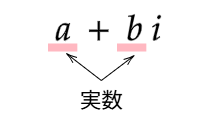
このとき,$a$ を実部(じつぶ),$b$ を虚部(きょぶ)という.もう少し簡単な表現にすると
(実数)+(実数) $i$
の形をしている数を複素数というのである.具体的には $2+3\,i$ や $-4+\sqrt5\,i$ や $-\dfrac{\sqrt2}3-\dfrac{\sqrt7}8\,i$ などである.こういった数の総称が複素数である.
いくつかの重要な補足
複素数 $a+b\,i$ は実数をも内包する新しい数
① $b=0$ のとき,$a+b\,i$ は $a$ とする.
つまり実数も複素数である.例えば5は $5+0\,i$,$-2$ は $-2+0\,i$ など.
② $b\neq0$ のとき,$a+b\,i$ を虚数という.
特に,$a=0$ のときは,$a+b\,i$ を $b\,i$ と表し,これを純虚数という.
例えば $2\,i$ や $-3\,i,\ \dfrac{\sqrt6}2i$ など.
③ 以上により,次のような包含関係になる:
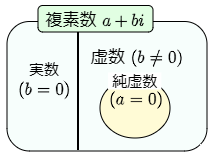
要するに,私たちが知っている数はすべて複素数であるということである.
2つの複素数が等しいとはどういうときをいうのか
2つの複素数 $a+b\,i$ と $c+d\,i$ が等しいとは,実部,虚部がそれぞれ等しいときをいう:
複素数の相等 \[a+b\,i=c+d\,i\iff a=c,\ b=d\]
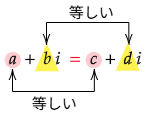
特に,$0$ は $0+0\,i$ であるから

