高校数学[総目次]
数学Ⅱ 第3章 図形と方程式
| スライド | ノート | 問題 | |
| 1. 座標平面上の点 | |||
| 2. 直線の方程式 | |||
| 3. 円の方程式 | |||
| 4. 円と直線 | |||
| 5. 軌跡と方程式 | |||
| 6. 不等式と領域 |

1.座標平面上の点
1.1 数直線上の点
数直線上の1点をPとするとき,Pに対応する実数

数直線上に2点A,Bをとり,線分ABを考える.この線分を
内分や外分の概念は,数直線上の線分に限らず,一般の線分に対して定義されるが,ここでは数直線上の線分に限定して話を進める.
内分点
数直線上の2点A,Bについて,線分AB上に点Pがあるとする.このとき,
注意
例えば

数直線上の2点
1°
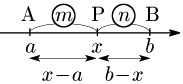
2°
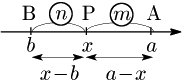
1°,2° ともに同じ結果となるから次が成り立つ:
内分点 数直線上の2点A
例 数直線上の2点
(1) 線分ABを
(2) 線分ABの中点
外分点
数直線上の2点A,Bについて,数直線上の線分ABの外側に点Qがあるとする.このとき,
内分のときと違って外分は少し難しい.数直線上の2点A,Bをとって線分ABを考えるところまでは同じなのであるが,内分のときには点Pを線分AB上にとったのに対し,外分では数直線上の線分AB以外のところ,つまり外側にとるのである.
外分を理解するために,「線分ABを
1° 線分ABを
数直線上のAに鉛筆を置き,そこから数直線に沿って2だけ進んだところにPを書く.ただしPは線分ABの外側にとる.そして鉛筆を浮かすことなくそこから1だけ移動させるとBにたどり着く.そのような点Pが線分ABを
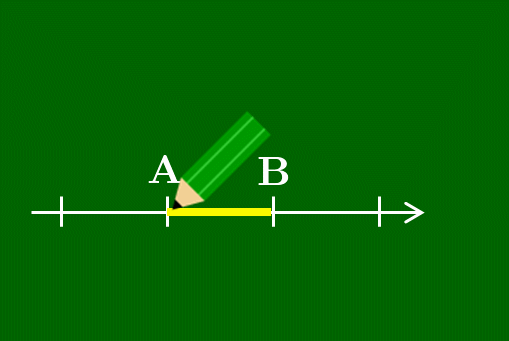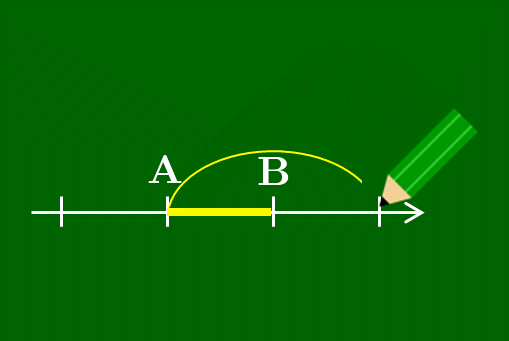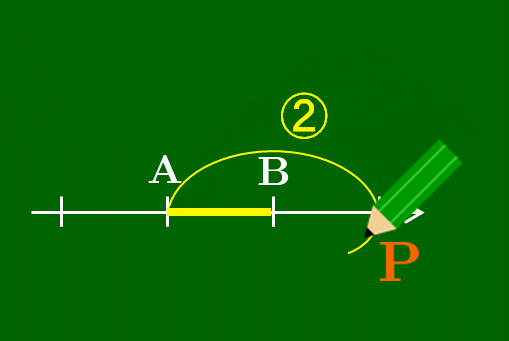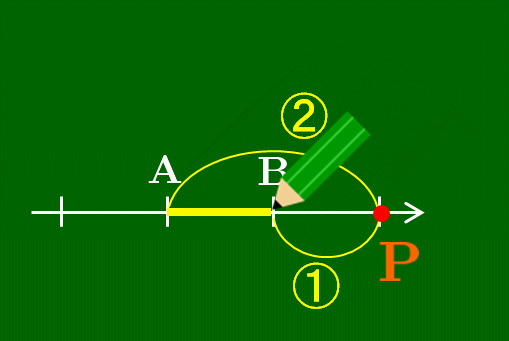
線分ABを
2° 線分ABを
数直線上のAに鉛筆を置き,そこから数直線に沿って1だけ進んだところにQを書く.ただしQは線分ABの外側にとる.そして鉛筆を浮かすことなくそこから2だけ移動させるとBにたどり着く.そのような点Qが線分ABを
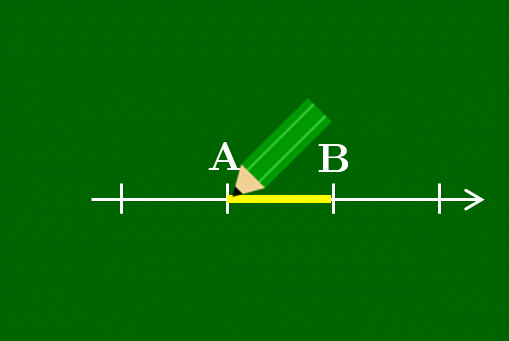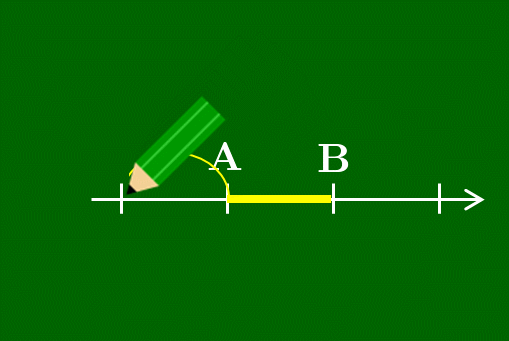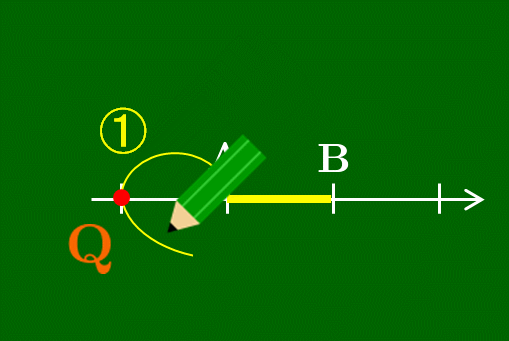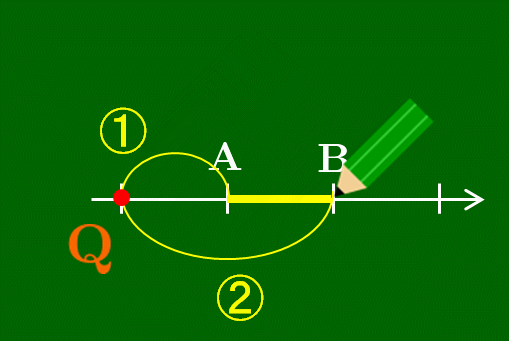
線分ABを
アニメーションの鉛筆の動きからわかるように,

数直線上の2点
1°
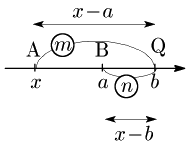
2°
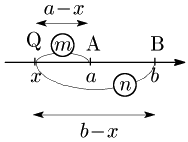
1°,2° ともに同じ結果となるから次が成り立つ:
外分点 数直線上の2点A
例 数直線上の2点
(1) 線分ABを
(2) 線分ABを

1.2 座標平面上の点
2点間の距離
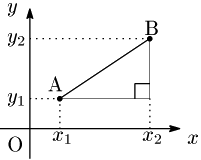
2点
となる.この式は,ABが
特に,点Bが原点
2点間の距離 平面上の2点A
例 A
内分点・外分点
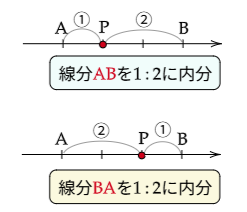
平面上の2点
1° 線分ABを
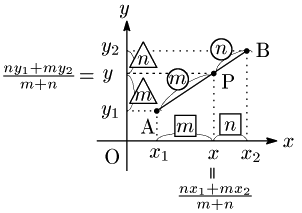
2° 線分ABを
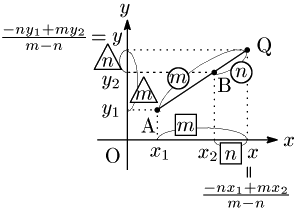
平行線と線分の比の関係を考えると,結局数直線上の2点の場合に帰着される.
まとめ 平面上の2点A
例 平面上の2点
(1)
(2) 中点
(3)
(4)
対称な点
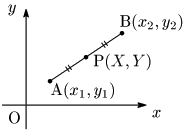
2点A
点Pは線分ABの中点
と捉える.
例題 点A
点P
よって,B
三角形の重心
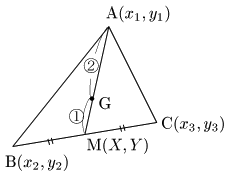
辺BCの中点をM
重心Gは,線分AMを
まとめ 3点A

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第3章 図形と方程式
| スライド | ノート | 問題 | |
| 1. 座標平面上の点 | |||
| 2. 直線の方程式 | |||
| 3. 円の方程式 | |||
| 4. 円と直線 | |||
| 5. 軌跡と方程式 | |||
| 6. 不等式と領域 |