高校数学[総目次]
数学Ⅲ 第1章 極限
| スライド | ノート | |
| 1. 数列の極限 | [無料] | |
| 2. 無限等比数列 | [無料] | |
| 3. 無限級数 | [会員] | |
| 4. 無限等比級数 | [会員] | |
| 5. 関数の極限 | [会員] | |
| 6. (sin x)/x の極限 | [会員] | |
| 7. 関数の連続性 | [会員] |

5.0 いくつかの例
例1
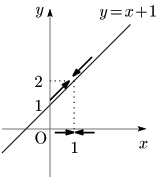
Q. $f(x)=x+1$ で,$x\to1$ のとき $f(x)\to ?$
A. $f(x)\to f(1)=2.$
例2
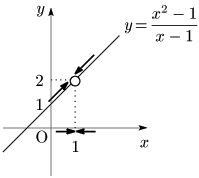
Q. $f(x)=\dfrac{x^2-1}{x-1}$ で,$x\to 1$ のとき $f(x)\to ?$
A. $f(x)=\dfrac{(x+1)(x-1)}{x-1}=x+1\to 2.$
5.1 関数の極限
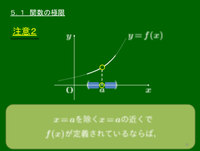
関数 $f(x)$ において,$x$ が $a$ と異なる値をとりながら限りなく $a$ に近付くとき,それに伴って $f(x)$ が限りなく $\alpha$ に近付く場合,「 $f(x)$ は $x\to a$ のとき $\alpha$ に収束する」といい, \[ \begin{array}{cl} &\displaystyle\lim_{x\to a}f(x)=\alpha,\\ \mbox{または}& x\to a\mbox{のとき}f(x)\to\alpha,\\ \mbox{または}& f(x)\to\alpha\ (x\to a) \end{array}\] で表す.また,$\alpha$ を $x\to a$ のときの $f(x)$ の極限値という.
注意
① $x\to a$ は「 $x$ が $a$ と異なる値をとりながら $a$
に近付く」のであって,「$x=a$ になる」ということではない.
② 従って(上の例2からもわかるように),$f(a)$ が定義されていなくても $\displaystyle\lim_{x\to a}f(x)$ が存在する場合がある.
補足
数列の極限($\cdots$①)と関数の極限($\cdots$②)の違い
① $\displaystyle\lim_{n\to\infty}a_n$:$n$ が自然数値をとりながら限りなく大きくなるときの$\{a_n\}$の挙動.
② $\displaystyle\lim_{x\to a} f(x)$:$x$ が実数値をとりながら限りなく $a$ に近付くときの $f(x)$ の挙動.
5.2 関数の極限値の性質
数列の場合と同様な性質が関数の極限でも成り立つ.もっとも数列のときがそうであったように,現段階では証明する手立てがない.いわゆる $\varepsilon -\delta$ 論法と呼ばれる考え方が必要で,大学での学びを待たなくてはならない.
$\displaystyle\lim_{x\to a} f(x)=\alpha,\ \lim_{x\to a}g(x)=\beta$ のとき,
① $\displaystyle\lim_{x\to a}\{kf(x)+lg(x)\}=k\alpha+l\beta$ ($k,\ l$ は定数)
② $\displaystyle\lim_{x\to a}f(x)g(x)=\alpha\beta$
③ $\displaystyle\lim_{x\to a}\frac{f(x)}{g(x)}=\frac \alpha\beta$ (ただし,$\beta\neq 0$)

5.3 不定形の極限
不定形を解消してから極限をとる.
例
Q. $\displaystyle\lim_{x\to 0}\frac 1{x^2}\left(x-\frac x{x+1}\right)\
(=\infty\cdot 0\ \ ??) $
A. $\dfrac 1{x^2}\left(x-\dfrac x{x+1}\right)=\dfrac
1{x^2}\cdot\dfrac{x^2}{x+1}=\dfrac1{x+1}\to 1\ (x\to 0)$
※ $h(x)=f(x)g(x)$ とおくと,$\displaystyle\lim_{x\to a}f(x)g(x)$ は,$\displaystyle\lim_{x\to a}h(x)$ であって,$f(x),\ g(x)$ をそれぞれ独立に極限操作してはならない.そうしてもよいのは $f(x),\ g(x)$ がともに収束するときだけ!(性質②)
次の性質はしばしば用いられる:
$\displaystyle\lim_{x\to a}\frac{f(x)}{g(x)}=\alpha$(収束),かつ $\displaystyle\lim_{x\to a}g(x)=0$ ならば, \[\lim_{x\to a}f(x)=0. \]
証明
$x\to a$ のとき,$\dfrac{f(x)}{g(x)},\ g(x)$ がともに収束するから, \[ \lim_{x\to a}f(x)=\lim_{x\to a}\frac{f(x)}{g(x)}\cdot g(x)=\alpha\cdot 0=0 \]
■
例題 $\displaystyle\lim_{x\to 1}\frac{a\sqrt x +b}{x-1}=2$ のとき,$a,\ b$ の値を求めよ.
答
$x\to 1$ のとき,$\dfrac{a\sqrt x +b}{x-1}$ が収束し,かつ分母が $x-1\to 0$ となるから,$\displaystyle\lim_{x\to 1}(a\sqrt x+b)=0$($\cdots$①)が必要.
よって,$a+b=0\ \therefore b=-a$.
故に, \[\lim_{x\to 1}\frac{a\sqrt x+b}{x-1}=\lim_{x\to 1}\frac{a(\sqrt x -1)}{x-1}=\lim_{x\to 1}\frac a{\sqrt x+1}=\frac a2.\] これが2に等しいから,$a=4.\ \therefore b=-4.$ ($\cdots$②)
補足
①は確かに $\displaystyle\lim_{x\to 1}\frac{a\sqrt x +b}{x-1}=2$ であるための必要条件.というのも,$\displaystyle\lim_{x\to 1}\frac{a\sqrt x+b}{x-1}$ の極限値の存在を仮定して導いたが,その値が2であることは用いていない.しかし②のところで,極限値が2であるように $a$ と $b$ を調整したのであるから,この時点で十分性も大丈夫.

5.4 関数の極限が発散するとき
$x\to a$ のとき,$f(x)$ が限りなく大きくなる場合,「$x\to
a$ のとき,$f(x)$ は正の無限大に発散する」といい,
\[\begin{align*}
&\lim_{x\to a}f(x)=\infty ,\\
\mbox{または}\ &x\to a\mbox{のとき,}f(x)\to\infty ,\\
\mbox{または}\ &f(x)\to\infty \ (x\to a)
\end{align*}\]
と書く.
同様に,$x\to a$ のとき,$f(x)<0$ で,$|f(x)|$ が限りなく大きくなるとき,「$x\to a$ のとき,$f(x)$ は負の無限大に発散する」という.(要するに,「限りなく小さくなる場合」だが,0に限りなく近付く場合との混乱を避けるため,このような表現となっている.)
\[ \lim_{x\to a}f(x)=\alpha\ (\mbox{収束}),\ \lim_{x\to a}f(x)=\infty,\ \lim_{x\to a}f(x)=-\infty \]のいずれでもない場合,$x\to a$ のときの $f(x)$ の極限はないという.
注意
極限がない,というのは $\displaystyle\lim_{x\to 0}\sin \frac 1x$ のような振動する場合だけではない.(次の右側極限と左側極限を参照.)
5.5 右側極限と左側極限
$x$ が $a$ より大きい値をとりながら限りなく $a$ に近付くとき,$x\to a+0$ と書く.同様に,$x$ が $a$ より小さい値をとりながら限りなく $a$ に近付くとき,$x\to a-0$ と書く.
特に,$a=0$ のときはそれぞれ $x\to +0$,$x\to -0$ と書く. $x\to a+0$ のときの $f(x)$ の極限を,「$x$ が $a$ に限りなく近付くときの右側極限」といい,$\displaystyle\lim_{x\to a+0}f(x)$ と書く.
同様に,$x\to a-0$ のときの$f(x)$ の極限を,「$x$ が $a$ に限りなく近付くときの左側極限」といい,$\displaystyle\lim_{x\to a-0}f(x)$ と書く.
$x$ が $a$ と異なる値をとりながら限りなく $a$ に近付く方法はいろいろある.(注意:右側と左側の2通りしかないのでは?ということではない.「方向」を言っているのではなく,具体的にどのような値をとりながら近付くかを考えている.)
例えば,$x\to 0$ のとき,次の数列$\{x_n\}$ はみな限りなく0に近付いていく:
\[x_n=\frac 1n,\ \frac1{2n},-\frac 1{3n},\ (-1)^n\frac 1n.\]
$x\to a$ というのは $a$ に限りなく近付くあらゆる近付き方を含んだ表現であり,従って
\[\lim_{x\to a}f(x)=\alpha \]というのは「$x$ が $a$ と異なる値をとりながら限りなく $a$ に近付くどのような近付き方をしても $f(x)$ は $\alpha$ に限りなく近付く」ということ,即ち$\displaystyle\lim_{n\to\infty}x_n=a$ であるどんな数列$\{x_n\}$ についても
\[ \lim_{n\to\infty} f(x_n)=\alpha\]
となることを意味している.
このように「$x\to a$」の意味を捉え直すと,次の定理が了解される:
定理 \[\begin{align*} \lim_{x\to a+0}&f(x)\ \mbox{と}\ \lim_{x\to a-0}f(x)\ \mbox{が異なる}\\ &\Longrightarrow\ x\to a\mbox{ のときの}\ f(x) \mbox{の極限はない} \end{align*}\]
例
$x$ 以下の最大の整数を $[x]$ (ガウス記号という)で表す.($[0.4]=0,\ [2]=2,\ [-1.5]=-2$ など.)
$f(x)=[x]$ とおくと,例えば \[\begin{align*} &0\leqq x<1\ \mbox{で}\ f(x)=0\\ &1\leqq x<2\ \mbox{で}\ f(x)=1 \end{align*}\] であるから, \[\lim_{x\to 1-0}f(x)=0,\ \lim_{x\to 1+0}f(x)=1\] 従って,$x\to 1$ のときの $f(x)$ の極限はない.
補足
「$\displaystyle\lim_{x\to a}f(x)=\alpha\ \Longrightarrow\ \lim_{x\to a+0}f(x)=\lim_{x\to a-0}f(x)=\alpha$」は当然成立するが,実は逆も成立し,従って次が成り立つ:
\[\lim_{x\to a}f(x)=\alpha \iff\ \lim_{x\to a+0}f(x)=\lim_{x\to a-0}f(x)=\alpha \]

5.6 $x\to \infty,\ x\to -\infty$ の極限
$x$ が実数値をとりながら限りなく大きくなるとき,それに伴って $f(x)$ が $\alpha$ に限りなく近付くとき, \[\lim_{x\to \infty}f(x)=\alpha \] と書く.$x\to -\infty$ の場合も同様.
例 $\displaystyle\lim_{x\to\infty}\frac 1x=0,\ \lim_{x\to -\infty}\frac 1x=0$
補足
$x\to\infty$ のときは,$x>0$ としてよい.同様に,$x\to -\infty$ のときは,$x<0$ としてよい.
例1 $\displaystyle\lim_{x\to -\infty}\sqrt{x^2}=\lim_{x\to -\infty}|x|=\lim_{x\to -\infty}(-x)=\infty$
例2 $\displaystyle\lim_{x\to -\infty}(\sqrt{x^2+2x\ }+x)=?$
\[\begin{align*} \mbox{× 与式}&=\lim_{x\to -\infty}\frac{2x}{\sqrt{x^2+2x\ }-x}\\ &=\lim_{x\to -\infty}\frac {2x}{x\sqrt{1+\frac 2x\ }-x}\ \ \ \mbox{←ここがダメ}\\ &=\lim_{x\to -\infty}\frac 2{\sqrt{1+\frac 2x\ }-1}\\ &=\frac 2{\sqrt 1-1}=\frac 20\ (?)\\ \mbox{〇 与式}&=\lim_{x\to -\infty}\frac{2x}{\sqrt{x^2+2x\ }-x}\\ &=\lim_{x\to -\infty}\frac {2x}{|x|\sqrt{1+\frac 2x\ }-x}\\ &=\lim_{x\to -\infty}\frac {2x}{-x\sqrt{1+\frac 2x\ }-x}\\ &=\lim_{x\to -\infty}\frac 2{-\sqrt{1+\frac 2x}-1}\\ &=\frac 2{-\sqrt 1-1}=-1\\ \mbox{〇}\ \ \ \ x=&-t \mbox{とおくと,}x\to -\infty\mbox{のとき,}t\to\infty .\\ \therefore \mbox{与式}&=\lim_{t\to \infty}(\sqrt{t^2-2t\ }-t)\\ &=\lim_{t\to\infty}\frac{-2t}{\sqrt{t^2-2t\ }+t}\\ &=\lim_{t\to\infty}\frac{-2t}{t\sqrt{1-\frac 2t\ }+t}\\ &=\lim_{t\to\infty}\frac{-2}{\sqrt{1-\frac 2t\ }+1}\\ &=\frac{-2}{\sqrt 1+1}=-1 \end{align*}\]

5.7 関数の極限値の大小関係
数列の極限と同様に,関数の極限においても次が成立:
$\displaystyle\lim_{x\to a}f(x)=\alpha,\ \lim_{x\to a}g(x)=\beta$ とする.$x$ が $a$ に十分近いとき,
① 常に $f(x)\leqq g(x)$ $\Longrightarrow$ $\alpha\leqq\beta$
② 常に $g(x)\leqq h(x)\leqq g(x)$ かつ $\alpha =\beta$
$\Longrightarrow$ $\displaystyle\lim_{x\to a}h(x)=\alpha$(はさみうちの原理)
例 $\displaystyle\lim_{x\to 0}x\sin\frac 1x=$?
答
$0\leqq \left|\sin\dfrac 1x\right|\leqq 1$ により,常に $0\leqq \left|x\sin\dfrac 1x\right|\leqq |x|$ である.
$\displaystyle\lim_{x\to 0}|x|=0$ であるから,はさみうちの原理により \[\begin{align*} &\lim_{x\to 0}\left|x\sin\frac 1x\right|=0.\\ \therefore\ &\lim_{x\to 0}x\sin\frac 1x=0. \end{align*}\]
注意
①に関連して,「常に $f(x)< g(x)$ $\Longrightarrow$ $\alpha<\beta$」は正しくない.
反例
$f(x)=|x|,\ g(x)=2|x|$ とすれば,$x\neq 0$ のとき,常に $f(x)<g(x)$.しかるに $\displaystyle\lim_{x\to 0}f(x)=0$,$\displaystyle\lim_{x\to 0}g(x)=0$ であるから $\alpha=\beta$.
次の定理も重要:
十分に大きい $x$ で常に $f(x)\leqq g(x)$のとき,$\displaystyle\lim_{x\to\infty}f(x)=\infty$ ならば,$\displaystyle\lim_{x\to\infty}g(x)=\infty .$(追い出しの原理)

このページで疑問は解決されましたか?
こちらから数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第1章 極限
| スライド | ノート | |
| 1. 数列の極限 | [無料] | |
| 2. 無限等比数列 | [無料] | |
| 3. 無限級数 | [会員] | |
| 4. 無限等比級数 | [会員] | |
| 5. 関数の極限 | [会員] | |
| 6. (sin x)/x の極限 | [会員] | |
| 7. 関数の連続性 | [会員] |