高校数学[総目次]
数学Ⅲ 第1章 極限
| スライド | ノート | |
| 1. 数列の極限 | [無料] | |
| 2. 無限等比数列 | [無料] | |
| 3. 無限級数 | [会員] | |
| 4. 無限等比級数 | [会員] | |
| 5. 関数の極限 | [会員] | |
| 6. (sin x)/x の極限 | [会員] | |
| 7. 関数の連続性 | [会員] |

7.0 はじめに
数学Ⅱの微分のところで次のような問題があった.
Q. 3次方程式 $x^3-4x+1=0$ が0と1の間に実数解をもつことを示せ.
一般に3次以上の方程式を高次方程式というが,高次方程式の基本解法は,まず発見的に解 $\alpha$ を1つ見つけて,左辺を $x-\alpha$ で割り,因数分解していくというものであった.この方程式の場合,$\alpha$ の候補は $\pm1$ である.ところが $x=1$ も $x=-1$ も解ではないからこの方程式は有理数解をもたない.(この点について詳しくはこちらを参照.) つまり,この方程式を解いて,解を具体的に求めることは簡単にはできないのである.しかしながら,単に実数解の存在を示すだけならば難しくない.方程式の左辺を $f(x)$ とおくと,
\[f(0)=1(>0),\ f(1)=-2(<0)\]
となって $f(0)$ と $f(1)$ は異符号であるから,グラフを考えると必ず0と1の間で $x$ 軸をまたがなければならない.すなわち $x$ 軸との共有点が存在するのである.このことは方程式の実数解の存在を示したことに他ならない.
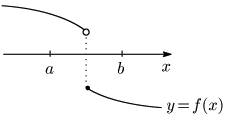
ところが別の方程式 $f(x)=0$ について, $f(x)$ のグラフが次のようであると,
$f(a)$ と $f(b)$ が異符号$\iff f(x)=0$ は $a$ と $b$ の間に実数解をもつ $\cdots$(☆)
とはいえない.グラフがつながっておらず,$x$ 軸と共有点をもっていないからである.つまり(☆)は無条件では成り立たない.グラフがつながっているという条件(仮定)が必要なのだ.それではグラフがつながっているというのを数学的に定式化するとどうなるのか.それが関数の連続性というものである.
7.1 関数が連続であるための条件
関数の連続性は定義域に属する各値に対して連続かどうかが決められるものである.例えば,ある関数 $f(x)$ は,$x=1$ では連続だけど $x=2$ では連続ではない等々.では連続かどうかを判定するにはどうしたらよいか.それは次に示す3つのステップをすべてクリアしたとき,連続であるというのである:
関数 $f(x)$ が $x=a$ で連続であるということは,次の3つが満たされているときをいう:
① $x=a$ は $f(x)$ の定義域に属する.
( $f(a)$ が定義されている.)
② 極限値 $\displaystyle\lim_{x\to a}f(x)$ が存在する.
③ $\displaystyle\lim_{x\to a}f(x)=f(a)$ である.
①を満たし,②,③のいずれか一方でも満たさない場合に,$f(x)$
は $x=a$ で不連続であるという.
従って例えば「関数 $\dfrac 1x$ は,$x=0$ で不連続である」とは言わない.($\dfrac 1x$ は $x=0$ で定義されていないから①を満たさない.)
例1
$f(x)=\left\{ \begin{array}{ll} 0&(x=0\ \mbox{のとき})\\ x^2+1&(x\neq 0\ \mbox{のとき}) \end{array}\right.$ について,$x=0$ での連続性を調べよ.
① $f(0)=0$ である.
② $\displaystyle\lim_{x\to0}f(x)=\lim_{x\to0}(x^2+1)=1$
③ $\displaystyle\lim_{x\to0}f(x)\ne f(0)$
よって,①,②を満たしているが,③を満たしていないので,$f(x)$ は $x=0$ で連続でない.
例2
$f(x)=x^2$ について,$x=0$ での連続性を調べよ.
① $f(0)=0$ である.
② $\displaystyle\lim_{x\to0}f(x)=\lim_{x\to0}x^2=0$
③ $\displaystyle\lim_{x\to0}f(x)= f(0)$
よって,①,②,③の全てを満たしているの,$f(x)$ は $x=0$ で連続である.
補足
$x=a$ で連続であるとは平たく言うと,$x=a$ のところでグラフがつながっている,あるいはジャンプがないということである.

7.2 連続性の性質
以下の性質はどれも違和感なく受け入れやすいものであると思われるが,厳密には全て証明が必要である.関数の極限値の性質を認めれば,これらはいずれも証明可能である.
関数 $f(x),\ g(x)$ が $x=a$ で連続のとき,次の関数も $x=a$ で連続である:
[1] $kf(x)+lg(x)$ ( $k,\ l$ は定数)
[2] $f(x)g(x)$
[3] $\dfrac{f(x)}{g(x)}$ (ただし $g(a)\neq 0$ )

7.3 連続関数
関数 $f(x)$ が,定義域のすべての $x$ で連続のとき,$f(x)$ は連続関数であるという.
補足
① 例えば関数 $\dfrac 1x$ は連続関数である.「$x=0$ で不連続なのでは??」…さにあらず.先に述べたように,関数の連続性は定義域内の各値でのもので,$x=0$ は関数 $\dfrac 1x$の定義域外の値であるから,そもそも連続性に関する議論の対象にならない.
② 関数 $x$ は連続関数であるから帰納的に $x^n$ ( $n$ は自然数)は連続関数である($\because$ 連続性の性質[2]).従って $x$ の整式 $a_0x^n+a_1x^{n-1}+\cdots +a_{n-1}x+a_n$ も連続関数である($\because$ 連続性の性質[1]).
一般に有理関数(整式 $+$ 分数式)は連続関数である($\because$ 連続性の性質[3]).

7.4 区間で連続
関数 $f(x)$ がある区間のすべての $x$ で連続のとき,$f(x)$ はその区間で連続であるという.
区間が開区間であれば,区間内の任意の値に対して両側極限を考えることができ,冒頭で示した連続例の判定方法が使える.しかし閉区間では,区間の両端の値において片側からの極限しか考えることができない.例えば閉区間 $[a,b]$ であれば,$x=a$ の右側極限を考えることはできるけれども左側極限を考えることはできない(もしくは考えない).あくまで閉区間 $[a,b]$ での関数の値しか考えないというスタンスをとるからである.そこで閉区間の連続性は,区間の両端の値に対しては片側極限だけを考えるのである.すなわち,閉区間で連続であるとは次のような状況をいう.
関数 $f(x)$ が「閉区間 $[a,\ b]$ で連続」とは
① 開区間 $(a,\ b)$ で連続
② $\left\{\begin{array}{cc} \displaystyle\lim_{x\to a+0}f(x)=f(a)\\[5pt]
\displaystyle\lim_{x\to b-0}f(x)=f(b) \end{array}\right.$
の2つが成立するときをいう.
例題1 関数 $f(x)=\sqrt{x-1}$ について,区間 $[1,2)$ における連続性を調べよ.
こたえ
解答例を表示する >例題2 $x$ を越えない最大の整数を $[x]$ で表す.関数 $f(x)=[x]$ について,区間 $(1,2]$ における連続性を調べよ.
こたえ
解答例を表示する >
7.5 連続関数の最大値・最小値の定理
閉区間で連続な関数には次の最大値・最小値の定理と呼ばれる定理が成り立つ:
最大値・最小値の定理 関数 $f(x)$ が閉区間で連続ならば,$f(x)$ はその区間で最大値と最小値をもつ.
仮定の検証
-
閉区間
もし(半)開区間ならば,例えば関数 $\tan x$ $\left(-\dfrac \pi 2<x<\dfrac\pi 2\right)$ などの反例がある.(最大値も最小値もない.) - 連続性
もし $f(x)$ が閉区間で連続でないなら,例えば閉区間$[0,1]$における関数 $x-[x]$ などの反例がある.(最大値がない.)
この定理は数学という学問においては重要な定理であるけれども,高校数学及び大学受験数学という観点からは,ほとんど利用されることはない.のちに出てくる平均値の定理をもし証明しようとすると,その過程でロルの定理と呼ばれるものを用いるが,更にさかのぼってロルの定理を証明しようとすると,この閉区間における連続関数の最大値・最小値の定理が登場するのである.程度の高い教科書にはこれらの証明が記載されている.

7.6 中間値の定理
中間値の定理 関数 $f(x)$ が閉区間 $[a,b]$ で連続で,$f(a)\neq f(b)$ ならば,$f(a)$ と $f(b)$ の間の任意の $k$ に対して \[f(c)=k,\ \ a<c<b\] となる $c$ が少なくとも1つ存在する.
残念ながら数学Ⅲの知識をもってしても,この定理を証明することはできない.「実数の連続性」と呼ばれる重要な考え方を大学で学んだのちに初めてこの定理の証明に取り掛かることができるのである.
この中間値の定理により,次の定理が導かれる:
定理 関数 $f(x)$ が閉区間 $[a,b]$ で連続で,$f(a)$ と $f(b)$ が異符号ならば,方程式 $f(x)=0$ は $a$ と $b$ の間に少なくとも1つの解をもつ.
例題 方程式 $xe^{-x}-4x+1=0$ は $0<x<1$ に実数解をもつことを示せ.
こたえ
解答例を表示する >
このページで疑問は解決されましたか?
こちらから数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第1章 極限
| スライド | ノート | |
| 1. 数列の極限 | [無料] | |
| 2. 無限等比数列 | [無料] | |
| 3. 無限級数 | [会員] | |
| 4. 無限等比級数 | [会員] | |
| 5. 関数の極限 | [会員] | |
| 6. (sin x)/x の極限 | [会員] | |
| 7. 関数の連続性 | [会員] |

