8. 平均値の定理(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅲ　第2章　微分法

	スライド	ノート	問題
1. 微分係数と導関数	[無料]
2. 合成関数の導関数	[無料]
3. 逆関数の微分法	[無料]		[会員]
4. 三角関数の導関数	[会員]
5. 対数関数・指数関数の導関数	[会員]
6. 媒介変数表示と導関数	[会員]
7. 陰関数の導関数	[会員]
8. 平均値の定理	[会員]
9. 関数の値の変化	[会員]
10. 関数の極大・極小	[会員]
11. 関数のグラフ	[会員]

8．平均値の定理

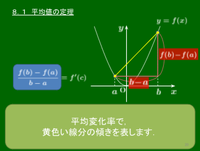
8.1 平均値の定理

平均値の定理とは？

　下図を見ると，曲線 $y=f(x)$ の $a< x< b$ における接線で，その傾きが2点 $(a,f(a))$ と $(b,f(b))$ を結ぶ線分の傾きと等しいものが(2つ)存在している．

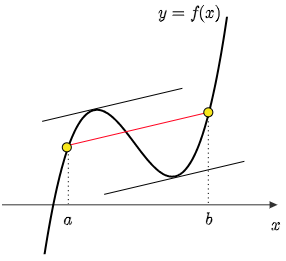
　こういったことを主張しているのが次に示す平均値の定理(mean-value theorem)であり，直感的にはとても受け入れやすい内容となっている．

平均値の定理 関数 $f(x)$ が，閉区間 $[a,\ b]$ で連続，開区間 $(a,\ b)$ で微分可能であるとき， \[ \frac{f(b)-f(a)}{b-a}=f'(c),\ \ a<c<b \] を満たす $c$ が存在する．

　この式の左辺は関数 $f(x)$ の $x$ の値が $a$ から $b$ まで変化したときの平均変化率で，グラフでは曲線 $y=f(x)$ 上の2点 $(a,f(a))$ と $(b,f(b))$ を結ぶ線分の傾きを表す．そして右辺は，$a$ と $b$ の間の値 $c$ における微分係数で， グラフでは $x=c$ における接線の傾きを表す．

　この定理は直感的にも理解しやすいものであると述べたが，証明の方はというと元を正していけば

連続関数の最大値・最小値の定理
$\Longrightarrow$ ロルの定理
$\Longrightarrow$ 平均値の定理

といった具合になっている．加えて最大値・最小値の定理やロルの定理は，高校の教科書においては証明なしに定理が紹介されるにとどまっている場合も多い．従ってこの辺りの内容をきっちり見ていくにはやはり大学課程の数学を待たねばなるまい．

補足

　$\dfrac{f(b)-f(a)}{b-a}=f'(c)$ を変形して

\[f(b)-f(a)=f'(c)(b-a)\]

となるが，これにより $f(b)-f(a)$ から $b-a$ を取り出すことができる． 入試問題でこの形の式が出てきたら「もしや平均値の定理が利用できるのでは？」とピンとくるようにしておきたい．

8.2 平均値の定理の不等式への応用

　平均値の定理の入試問題への応用としては，次に紹介する不等式への応用と，次節に紹介する漸化式への応用が2大応用例となっている．

平均値の定理の2大応用例～その1

例題 [不等式への応用]
$0<a<b$ のとき，$\dfrac 1b < \dfrac{\log b-\log a}{b-a} < \dfrac 1a$ を示せ．

　$f(x)=\log x$ とおくと，$f(x)$ は閉区間 $[a,b]$ で連続，開区間 $(a,b)$ で微分可能であるから，平均値の定理により， \[\frac{f(b)-f(a)}{b-a}=f'(c),\ a<c<b\] を満たす $c$ が存在する．$f'(x)=\dfrac1x$ で，$0\! < \! a \! < \! b$ により $\dfrac1b < \dfrac1c < \dfrac1a$ だから， \[\frac1b<f'(c) < \frac1a\] \[\therefore \frac1b < \frac{f(b)-f(a)}{b-a} < \frac1a\]

■

8.3 平均値の定理の漸化式への応用

平均値の定理の2大応用例～その2

　漸化式によって定義された数列の極限について，その漸化式から一般項が導けて，一般項を元に極限を考えることができる場合と，そもそも漸化式から一般項を導くのが困難で，別な方法によって数列の極限を考えなければならない場合がある．後者のように解けない漸化式によって定義された数列の極限を考える際に平均値の定理が突破口を開いてくれる場合がある．

例題 [漸化式への応用]
関数 $f(x)={\sqrt2}^{\,x}$ について
(1)　$x_1,x_2\leqq2\ (x_1\neq x_2)$ のとき，$|f(x_2)-f(x_1)|<(\log2)\cdot |x_2-x_1|$ が成り立つことを証明せよ．
(2)　$a_1=\sqrt2,\ a_{n+1}=f(\,a_n)$ で与えられる数列 $\{a_n\}$ について $\displaystyle \lim_{n\to\infty}a_n$ を求めよ．

こたえ

(1)　$f'(x)=\sqrt2^{\,x}\log\sqrt2$

$f(x)$ は閉区間 $[x_1,x_2]$ (または $[x_2,x_1]$)で連続，開区間 $(x_1,x_2)$ (または $(x_2,x_1)$)で微分可能であるから平均値の定理により $\dfrac{f(x_2)-f(x_1)}{x_2-x_1}= f'(c)$ すなわち

\[\frac{f(x_2)-f(x_1)}{x_2-x_1}= \sqrt2^{\,c}\log\sqrt2\]

を満たす $c$ が $x_1$ と $x_2$ の間に存在する．この右辺について，$f'(x)$ は実数全体で単調に増加し，$c<2$ であるから

\[0<f'(c)< f'(2)= \sqrt2^{\,2}\log\sqrt2=\log2\]

　従って

\[\left|\frac{f(x_2)-f(x_1)}{x_2-x_1}\right|<\log2\]

\[\therefore |f(x_2)-f(x_1)|<(\log2)\cdot|x_2-x_1|\]

■

(2)　「すべての自然数 $n$ について $a_n\leqq2$ …(☆)」であることを数学的帰納法で示す．(これを示しておかないと，(1)の不等式が利用できない．)

[1]　$n=1$ のとき，$a_1=\sqrt2<2$ だから成り立つ．

[2]　$n=k$ のときの成立を仮定すると，底の $\sqrt2$ が1より大きいから，

\[a_{k+1}=\sqrt2^{\,a_k}\leqq\sqrt2^{\,2}=2\]

　従って $n=k+1$ のときも成立するから(☆)が示された．

　$f(2)=2,\ a_n=f(a_{n-1})$ により

\[|2-a_n|=|f(2)-f(a_{n-1})|<(\log2)\cdot|2-a_{n-1}|\]

\[\therefore \ \ |2-a_n|<(\log2)\cdot|2-a_{n-1}|\]

　この関係を繰り返し用いて

\[\begin{align*} |2-a_n|&<(\log2)\cdot|2-a_{n-1}|\\[5pt] &<(\log2)^2\cdot|2-a_{n-2}|\\[5pt] &<\cdots\\[5pt] &<(\log2)^{n-1}\cdot|2-a_1| \end{align*}\]

\[\therefore\ \ (0<\,)\, |2-a_n|<(\log2)^{n-1}\cdot|2-\sqrt2|\]

　$0<\log2<\log e=1$ より，この右辺は $n\to\infty$ のとき0に収束するから，はさみうちの原理により

\[|2-a_n|\to0\ \ (n\to\infty)\]

\[\therefore \ \ \lim_{n\to\infty}a_n=2\]

補足

　$\sqrt2^{\sqrt2^{\sqrt2^{\cdots}}}=2$ となることが示されたことになる．

---

高校数学[総目次]

数学Ⅲ　第2章　微分法

	スライド	ノート	問題
1. 微分係数と導関数	[無料]
2. 合成関数の導関数	[無料]
3. 逆関数の微分法	[無料]		[会員]
4. 三角関数の導関数	[会員]
5. 対数関数・指数関数の導関数	[会員]
6. 媒介変数表示と導関数	[会員]
7. 陰関数の導関数	[会員]
8. 平均値の定理	[会員]
9. 関数の値の変化	[会員]
10. 関数の極大・極小	[会員]
11. 関数のグラフ	[会員]