6. 媒介変数表示と導関数(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅲ　第2章　微分法

	スライド	ノート
1. 微分係数と導関数	[無料]
2. 合成関数の導関数	[無料]
3. 逆関数の微分法	[無料]
4. 三角関数の導関数	[会員]
5. 対数関数・指数関数の導関数	[会員]
6. 媒介変数表示と導関数	[会員]
7. 陰関数の導関数	[会員]
8. 平均値の定理	[会員]
9. 関数の値の変化	[会員]
10. 関数の極大・極小	[会員]
11. 関数のグラフ	[会員]

6．媒介変数表示と導関数

6.1 媒介変数表示と導関数

　例として $y=x^2-2x+3$ で表される曲線を $C$ とする．$C$ はおなじみ放物線である．この曲線上の点には

\[(-1,6),\ (0,3),\ (1,2) \]

などがある．ここで，$x$ が $t$ を用いて $x=t+1$ と表されているならば，曲線の式に代入すると $y$ は

\[y=(t+1)^2-2(t+1)+3=t^2+2\]

と表せる．すなわち曲線 $C$ 上の点が

\[\left\{\begin{array}{l} x=t+1\\[5pt] y=t^2+2 \end{array}\right.\ \ \cdots(*)\]

というように $t$ を用いて表せる．先に挙げた $C$ 上の3点はそれぞれ $t=-2,\ -1,\ 0$ における値である．つまり $(*)$ でも同じ曲線を表すことができるのである．

　このように，曲線上の点 $(x,y)$ が， 文字 $t$ を用いて表されるとき，これを媒介変数を $t$ とする曲線の媒介変数表示，あるいはパラメータを $t$ とする曲線のパラメータ表示という．

　上にあげた $(*)$ は曲線 $C$ のパラメータ表示の一例であって，同じ曲線を表すパラメータ表示の仕方は無数にある．極端な例として

\[\left\{\begin{array}{l} x=t\\[5pt] y=t^2-3t+2 \end{array}\right.\]

も一応曲線のパラメータ表示である．

　さて，$(*)$ で $x$ の式を $t$ について解き， $x$ と $y$ の順序を入れ替えて

\[\left\{\begin{array}{l} y=t^2+2\\[5pt] t=x-1 \end{array}\right.\]

と表すと，関数 $y=x^2-2x+3$ はこの2つの関数の合成関数とみなすことができる．このとき，$\dfrac{dy}{dt}=2t$，$\dfrac{dt}{dx}=1$ であるから，合成関数の導関数の公式により

\[\frac{dy}{dx}=\frac{dy}{dt}\cdot\frac{dt}{dx}=2t\cdot1=2t=2(x-1)\]

となる．当然ながらこの結果は

\[\frac{dy}{dx}=\frac d{dx}(x^2-2x+3)=2x-2\]

と一致する．

　もう少し違う例を見てみよう．

\[\left\{\begin{array}{l} x=t^3+t^2+t\\[5pt] y=t^2 \end{array}\right.\]

　これだと $t$ を $x$ の式で表すのは容易ではないから $y=(x$ の式) の形で表すことは極めて困難である．従って $\dfrac{dy}{dx}$ を従来通り「 $x$ の式を微分する」という方法で求めることはできそうにない．しかし今 $t=(x$ の式) というように表せたとして，$x$ の関数 $y$ を

\[\left\{\begin{array}{l} y=t^2\\[5pt] t=(x\mbox{の式}) \end{array}\right.\]

の合成関数とみなそう．合成関数の導関数により

\[\frac{dy}{dx}=\frac{dy}{dt}\cdot\frac{dt}{dx}=2t\cdot\frac{dt}{dx}\]

　$\dfrac{dy}{dt}$ の方は $2t$ として解決だが， $\dfrac{dt}{dx}$ の方は $t$ が $x$ の関数として表せないのだから，計算できない．しかし，逆関数の微分法により

\[\frac{dt}{dx}=\frac1{\dfrac{dx}{dt}}=\frac1{3t^2+2t+1}\]

とできるから，結局

\[\frac{dy}{dx}=2t\cdot\frac1{3t^2+2t+1}=\frac{2t}{3t^2+2t+1}\]

となり，$\dfrac{dy}{dx}$ を求めることができた．ただし，これまで $\dfrac{dy}{dx}$ といえば $x$ の式であったが，今回のケースではその表現は望めない．しかし　$x$ や $y$ の値から $t$ の値を決めることができるならば，微分係数を上の式から計算することができるのである．

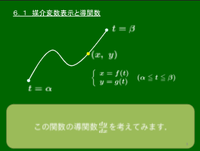
　一般に，曲線上の点 $(x,y)$ が媒介変数(パラメータ) $t$ を用いて \[\left\{\begin{array}{l} x=f(t)\\ y=g(t) \end{array}\right.\ (\alpha\leqq t\leqq\beta)\] のように表されているとき，

\[\begin{align*} \frac{dy}{dx}&=\frac{dy}{dt}\cdot\frac{dt}{dx}\ (\because\mbox{合成関数の導関数})\\[5pt] &=\frac{dy}{dt}\cdot\frac1{\dfrac{dx}{dt}}\ (\because\mbox{逆関数の微分法})\\[5pt] &=\frac{\ \dfrac{dy}{dt}\ }{\dfrac{dx}{dt}}\\[5pt] &=\frac{g'(t)}{f'(t)} \end{align*}\]

と表されるのである．

例題　$x$ の関数 $y$ が，$\left\{\begin{array}{l}x=t+1\\y=t^2\end{array}\right.$ で表されるとき，$x=3$ における微分係数を求めよ．

　解答例を表示する >

\[ \frac{dy}{dx}=\frac{dy/dt}{dx/dt}=\frac{2t}1=2t\ \bigl[=2(x-1)\bigr]\] 　$x=3$ のとき，$t=2$ であるから， \[\left.\frac{dy}{dx}\right|_{x=3}=2\cdot2=\underline{4}\]

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

---

高校数学[総目次]

数学Ⅲ　第2章　微分法

	スライド	ノート
1. 微分係数と導関数	[無料]
2. 合成関数の導関数	[無料]
3. 逆関数の微分法	[無料]
4. 三角関数の導関数	[会員]
5. 対数関数・指数関数の導関数	[会員]
6. 媒介変数表示と導関数	[会員]
7. 陰関数の導関数	[会員]
8. 平均値の定理	[会員]
9. 関数の値の変化	[会員]
10. 関数の極大・極小	[会員]
11. 関数のグラフ	[会員]