このページにある内容は，こちらのスライド(会員向け)でわかり易く説明しています．

※PC環境なら全画面表示でより見やすく，よりわかりやすい！

高校数学[総目次]

数学Ⅲ　第2章　微分法

  スライド ノート
1. 微分係数と導関数 [無料]  
2. 合成関数の導関数 [無料]  
3. 逆関数の微分法 [無料]  
4. 三角関数の導関数 [会員]  
5. 対数関数・指数関数の導関数 [会員]  
6. 媒介変数表示と導関数 [会員]  
7. 陰関数の導関数 [会員]  
8. 平均値の定理 [会員]  
9. 関数の値の変化 [会員]  
10. 関数の極大・極小 [会員]  
11. 関数のグラフ [会員]  

7．陰関数の導関数

7.1 陰関数の導関数

　例えば，関数 $y=2x^2+3x+4\ (\cdots$①) について，この式を変形すると $2x^2+3x-y+4=0\ (\cdots$②) と表せる．①のように $y=(x$ の式) の形を陽関数といい，②のように，$(x$ と $y$ の式)$=0$ の形を陰関数という．

　①において， $y$ を $x$ で微分すると

\[y’\left(=\frac{dy}{dx}\right)=4x+3\]

となるのはよいであろう．一方②のような形で与えられていて，$\dfrac{dy}{dx}$ を求めようとすると，もちろん①のように $y$ について解いてから(陽関数にしてから)微分することもできるが，それをあとまわしにした次のようなやり方もある：

　②の両辺を $x$ で微分すると

\[4x+3-y’=0\]

\[\therefore y’=4x+3\]

　当然ながら同じ結果が得られた．$y=(x$ の式) とするのが先か，微分するのが先かの違いはあれど，結果としてはどちらも正しい導関数が得られるのである．つまり，この例を通して理解しておきたいのは，微分をするのに何も $y$ について解かれた式，すなわち $y=(x$ の式) となっていなければならないということはない，ということである．

$y=(x$ の式) となっていなくても微分はできる

　別の例として $x^2+y^2=1$ をみてみよう．おなじみ円の方程式である．これも $x$ の値が決まれば $y$ の値が決まるという意味で $y$ は $x$ の関数である．とはいうものの，これまで関数といえば $x$ の値に対して $y$ の値がただ1つ決まるものを関数(これを1価関数という)と呼んできたのであって，$x^2+y^2=1$ のように定義域のほぼ全域で1つの $x$ の値に対して $y$ の値が複数対応しているようなもの(これを多価関数という)は，これまでの意味での関数ではない．

　実際，$x^2+y^2=1$ を $y$ について解くと

\[y^2=1-x^2\]

\[\therefore y=\pm\sqrt{1-x^2}\]

　従って $-1<x<1$ のとき， $y$ は $\sqrt{1-x^2}$ と $-\sqrt{1-x^2}$ の2つが対応する．

　さて，この関数の導関数を求めてみよう．まず，$y=\sqrt{1-x^2}$ より

\[y’=-\frac x{\sqrt{1-x^2}}\]

　ここで分母の $\sqrt{1-x^2}$ が $y$ であるから

\[y’=-\frac xy\]

とも書けることに注意しておこう．これまで導関数とくれば $x$ の式であったことからすると強い違和感があるかもしれない．しかし導関数を $x$ の情報だけで表そうとすると式がやや大きく膨らんでしまうところ，$x$ と $y$ の2つの情報を用いれば，ずっとコンパクトな式になるというメリットがあるのだ．そしてメリットはそれだけではない．

メリット①$y$ も用いれば，導関数は小さくまとまる．

　$y=-\sqrt{1-x^2}$ の方も微分してみると

\[y’=\frac x{\sqrt{1-x^2}}\]

　分母の　$\sqrt{1-x^2}$ が $-y$ であるから

\[y’=-\frac xy\]

となる．これが $x$ と $y$ の2つの情報を用いて導関数を表すもう1つのメリットだ．どういうことかといえば，微分する元となる式は $y=\sqrt{1-x^2}$ と $y=-\sqrt{1-x^2}$ で異なっていたにもかかわらず，それらの導関数は $x$ と $y$ の両方を用いて表せば，どちらも同じ式 $y’=-\dfrac xy$ になるのである！

メリット②$y$ も用いれば，式が1本化できる．

　ところで，$x^2+y^2=1$ もこの形のまま微分してみることにしよう．この式の両辺を $x$ で微分すると

\[2x+2yy’=0\]

\[\therefore y’=-\frac xy\]

　なんと先ほど導いた $x$ と $y$ を用いた導関数の式が，いとも簡単に導かれたではないか！

　そしてこのことは一般にもいえて，陰関数はその形のまま( $y=\cdots$ としないで)微分した方がラクな場合が多い．

陰関数の微分法

$y=\cdots$ としないでその形のまま微分する

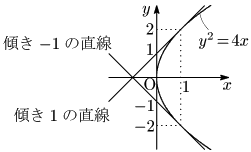
例題　$y^2=4x\ \cdots$① のとき，$x=1$ における微分係数を求めよ．

こたえ

　解答例を表示する >

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]

数学Ⅲ　第2章　微分法

  スライド ノート
1. 微分係数と導関数 [無料]  
2. 合成関数の導関数 [無料]  
3. 逆関数の微分法 [無料]  
4. 三角関数の導関数 [会員]  
5. 対数関数・指数関数の導関数 [会員]  
6. 媒介変数表示と導関数 [会員]  
7. 陰関数の導関数 [会員]  
8. 平均値の定理 [会員]  
9. 関数の値の変化 [会員]  
10. 関数の極大・極小 [会員]  
11. 関数のグラフ [会員]