9. 関数の値の変化(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅲ　第2章　微分法

	スライド	ノート
1. 微分係数と導関数	[無料]
2. 合成関数の導関数	[無料]
3. 逆関数の微分法	[無料]
4. 三角関数の導関数	[会員]
5. 対数関数・指数関数の導関数	[会員]
6. 媒介変数表示と導関数	[会員]
7. 陰関数の導関数	[会員]
8. 平均値の定理	[会員]
9. 関数の値の変化	[会員]
10. 関数の極大・極小	[会員]
11. 関数のグラフ	[会員]

9．関数の値の変化

9.1 関数の増減

　閉区間 $[a,b]$ において，$a\leqq x_1<x_2\leqq b$ を満たすどんな $x_1,\,x_2$ についても， \[ f(x_1)<f(x_2)\] が成り立つとき，$f(x)$ は閉区間 $[a,b]$ で単調に増加するという．
　(単調に減少する場合も同様に定義される．)

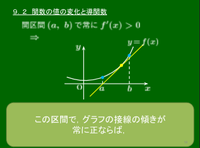
9.2 関数の値の変化と導関数

　関数 $f(x)$ は閉区間 $[a,b]$ で連続，開区間 $(a,b)$ で微分可能であるとする．このとき，次が成り立つ：

導関数の符号と単調性[1] 開区間 $(a,\ b)$ で常に$f'(x)>0$ $\Longrightarrow$ $f(x)$は閉区間 $[a,\ b]$ で単調に増加する．
[2] 開区間 $(a,\ b)$ で常に $f'(x)<0$ $\Longrightarrow$ $f(x)$ は閉区間 $[a,\ b]$ で単調に減少する．
[3] 開区間 $(a,\ b)$ で常に $f'(x)=0$ $\Longrightarrow$ $f(x)$ は閉区間 $[a,\ b]$ で定数である．

証明

[1]

　任意の $x_1,x_2\in[a,b]$，$x_1<x_2$ をとる：

$a\leqq x_1<x_2\leqq b$
($a=x_1$，または $x_2=b$ かもしれないことに注意)

　$f(x)$ は閉区間 $[a,b]$ で連続，開区間 $(a,b)$ で微分可能であったから，その一部である閉区間 $[x_1,x_2]$ で連続，開区間 $(x_1,x_2)$ でも微分可能．従って平均値の定理により， \[\frac{f(x_2)-f(x_1)}{x_2-x_1}=f'(c)\ \ (x_1< c< x_2)\] を満たす $c$ が存在する．$f(x)$ は開区間 $(a,b)$ で常に $f'(x)>0$ であったから，その一部である開区間 $(x_1,x_2)$ でも常に $f'(x)>0$．従って $f'(c)>0$．故に， \[f(x_2)-f(x_1)=f'(c)(x_2-x_1)>0\] \[\therefore f(x_2)>f(x_1)\] 　従って[1]が示された．

[2]

　[1] と同様に示される．

[3]

　任意の $x_1,x_2\in[a,b]$，$x_1<x_2$ について，平均値の定理の右辺が常に0であるから， \[f(x_1)=f(x_2)\] 　ここで，$x_1$ を $a$ に固定しておくと，任意の $x_2\in(a,b]$ について， \[f(a)=f(x_2)\] となる．従って $f(x)$ はこの区間で定数関数である．

■

注意

　開区間 $(a,b)$ で $f'(x) > 0$ であれば，この区間で単調に増加するのは当然として，この定理は両端も含めての単調性を主張している．

例題　$e^x > x+1\ (x>0)$ を示せ．

　$f(x)=e^x-(x+1)$ とおき，$f(x)>0\ (x>0)$ を示す． \[f'(x)=e^x-1>0\ (\because x>0)\] 　よって，$f(x)$ は $x\geqq0$ で単調に増加するから， \[f(x)>f(0)=0\]

■

補足

　$f'(x)\geqq0,\ f'(x)\leqq0$ (不等号の下に「$=$」がつく)場合について．
　開区間 $(a,b)$ で $a < c < b$ なる $c$ でのみ $f'(c)=0$ で，残りの値では常に $f'(x) > 0$ となるならば，閉区間 $[a,c]$ と $[c,b]$ で $f(x)$ は単調に増加するのであるから，2つの閉区間を結合した閉区間 $[a,b]$ においても $f(x)$ は単調に増加することがわかる．

補足の例

　$f(x)=x^3$ のとき，$f'(x)=3x^2\ (\,x\geqq0)$ により，増減表は次のようになる：

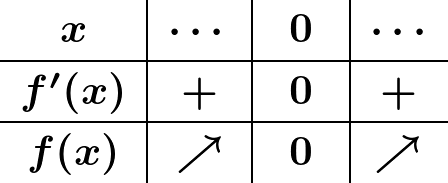
　従って $f(x)=x^3$ は実数全体で単調に増加する．

定理　$f(x),\ g(x)$ が閉区間 $[a,\ b]$ で連続で、開区間 $(a,\ b)$ で微分可能かつ常に $f'(x)=g'(x)$ ならば，閉区間 $[a,\ b]$ で \[ f(x)=g(x)+C\ \ (C\mbox{は定数}) \]

証明

　$F(x)=f(x)-g(x)$ とおくと，$F(x)$は閉区間 $[a,b]$ で連続，開区間 $(a,b)$ で微分可能であり，常に \[\begin{align*} F'(x)&=f'(x)-g'(x)\\ &=0\ \ \ \ (\because f'(x)=g'(x)\ ) \end{align*}\] であるから，この節冒頭の「導関数の符号と単調性」の定理により， \[F(x)=C\ (\mbox{定数})\] 　従って， \[f(x)-g(x)=C\] \[\therefore f(x)=g(x)+C\]

■

高校数学[総目次]

数学Ⅲ　第2章　微分法

	スライド	ノート
1. 微分係数と導関数	[無料]
2. 合成関数の導関数	[無料]
3. 逆関数の微分法	[無料]
4. 三角関数の導関数	[会員]
5. 対数関数・指数関数の導関数	[会員]
6. 媒介変数表示と導関数	[会員]
7. 陰関数の導関数	[会員]
8. 平均値の定理	[会員]
9. 関数の値の変化	[会員]
10. 関数の極大・極小	[会員]
11. 関数のグラフ	[会員]