10. 関数の極大・極小(ノート)
スライドで学ぶ高校数学

このページにある内容は，こちらのスライド でわかり易く説明しています．

PC環境なら全画面表示でより見やすく，よりわかりやすい！
全画面表示の仕方は こちら

数学Ⅲ　第2章　微分法

	スライド	ノート	問題
1. 微分係数と導関数	[無料]
2. 合成関数の導関数	[無料]
3. 逆関数の微分法	[無料]		[会員]
4. 三角関数の導関数	[会員]
5. 対数関数・指数関数の導関数	[会員]
6. 媒介変数表示と導関数	[会員]
7. 陰関数の導関数	[会員]
8. 平均値の定理	[会員]
9. 関数の値の変化	[会員]		[会員]
10. 関数の極大・極小	[会員]
11. 関数のグラフ	[会員]

10．関数の極大・極小

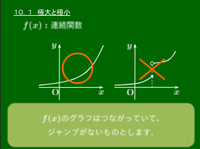
10.1 極大・極小

　極大・極小については数学Ⅱ で既出である．極大や極小については数学Ⅱの方で詳細に説明したのでそちらを参照されたい．

極大値・極小値の定義

　関数 $f(x)$ は連続とする．
　$x=a$ を含む開区間で，どんな $x\,(\neq a)$ についても
　　$f(a)>f(x)$ のとき，$f(a)$ を $f(x)$ の極大値
　　$f(a)<f(x)$ のとき，$f(a)$ を $f(x)$ の極小値
という．また，極大値と極小値をあわせて極値という．

注意

　極大・極小は，微分可能性とは無関係である．例えば，関数$f(x)=|x|$ は，$x=0$ で微分可能ではないが，$x=0$ で極小となっている．

10.2 $f(a)$ が極値であるための必要条件

　微分可能な関数 $f(x)$ が $x=a$ で極値をとるとする．このとき $f'(a)=0$ が成り立つ．これは数学Ⅱの微分法のときにもお世話になっていたものである．$f'(a)=0$ は $f(x)$ が $x=a$ で極値をとるための必要条件である．

定理　$f(x)$ が微分可能であるとき，

$f(a)$ が極値 $\Longrightarrow\ f'(a)=0$

発展的補足

　$f(x)$ が整式の場合などほとんど明らかと思われるこの定理．実際教科書にも証明が書かれていない．しかし例えば次の関数は $x=0$ で極小となるが，$x=0$ の付近で無限回振動するから，本当に $f'(0)=0$ なのかは明らかではない．（この関数については次節10.3に詳細な説明有．）

\[f(x)=\left\{\begin{array}{ll} x^2\left(\cos\dfrac1x+2\right)&(x\neq0)\\[5pt] 0&(x=0) \end{array}\right.\]

　そこでこの定理を証明する．

証明

　ある開区間で微分可能な関数 $f(x)$ が，区間内の $x=a$ で極大になるとすれば，区間内の任意の $x$ について

$f(x)\leqq f(a)\ \cdots$ ①

が成り立つ．$x=a$ で微分可能であるから

\[\lim_{x\to a}\frac{f(x)-f(a)}{x-a}=f'(a)\]

となるが，①より左辺の分子は常に0以下であることに注意する．ここで $x\to a+0$ のとき，$x-a\to +0$ であるから

\[\lim_{x\to a+0}\frac{f(x)-f(a)}{x-a}\leqq 0\ \ \ \therefore f'(a)\leqq0\]

　一方，$x\to a-0$ のとき，$x-a\to -0$ であるから

\[\lim_{x\to a-0}\frac{f(x)-f(a)}{x-a}\geqq 0\ \ \ \therefore f'(a)\geqq0\]

　従って，$f'(a)\leqq0$ かつ $f'(a)\geqq0$ となるから， $f'(a)=0$．

　$x=a$ で極小となる場合も同様である．

■

注意

　逆 $(\Leftarrow)$ は成り立たない．
　(反例)　$f(x)=x^3$ のとき，$f'(x)=3x^2$ より $f'(0)=0$．しかるに $f(0)$ は極値ではない．

10.3 $f(a)$ が極値であるための十分条件

　前節10.2では，「$f(a)$ が極値である」というのが仮定で，「$f'(a)=0$」というのが結論であった．今度は逆に，「$f(a)$ が極値である」が結論にくるような命題を見てみよう．「　　　　は $f(a)$ が極値であるための十分条件である」の下線部に入るようなものである．

定理　$x=a$ を含むある開区間で $f(x)$ は微分可能かつ $f'(a)=0$ とする．この区間内において，

① $x< a$ で $f'(x) > 0,\ a < x$ で $f'(x) < 0$
　　$\Longrightarrow f(a)$ は極大値

② $x<a$ で $f'(x) < 0,\ a < x$ で $f'(x) > 0$
　　$\Longrightarrow f(a)$ は極小値

証明

①　$x<a$ で $f'(x)>0$ であるから，区間内の $x\leqq a$ で $f(x)$ は単調に増加する．従って区間内のすべての $x\,(< a)$ で $f(x)< f(a)$．
　また，$x>a$ で $f'(x)<0$ であるから，区間内の $x\geqq a$ で $f(x)$ は単調に減少する．従って区間内のすべての $x\,(> a)$ で $f(x)< f(a)$．
　従って，この開区間において $f(a)$ は最大値となるから極大値である．

②　①と同様に示される．

■

発展的注意

　逆 $(\Leftarrow)$ は成り立たない．
　(反例)

\[f(x)=\left\{ \begin{array}{ll} x^2\left(\cos\dfrac1x+2\right)&(x\neq0\mbox{のとき})\\[5pt] 0&(x=0\mbox{のとき}) \end{array}\right.\] 　

　この関数 $f(x)$ は $x\ne0$ のとき，

\[\begin{align*} f'(x)&=2x\left(\cos\frac1x+2\right)+x^2\left\{-\sin\frac1x\cdot\left(-\dfrac1{x^2}\right)\right\}\\[5pt] &=2x\left(\cos\frac1x+2\right)+\sin\dfrac1x \end{align*}\]

であるから微分可能．また $x=0$ でも微分可能で，$f'(0)=0$．実際，

\[\begin{align*} \lim_{x\to0}\frac{f(x)-f(0)}{x-0}&=\lim_{x\to0}\dfrac{x^2\left(\cos\frac1x+2\right)}x\\[5pt] &=\lim_{x\to0}x\left(\cos\dfrac1x+2\right)\\[5pt] &=0\ \ (\because\mbox{はさみうちの原理}) \end{align*}\]

　また，$-1\leqq\cos\dfrac1x\leqq1$ より $1\leqq\cos\dfrac1x+2\leqq3$ であるから，$f(x)$ のグラフは放物線 $y=x^2$ の上側かつ $y=3x^2$ の下側となり，$f(0)=0$ と定義されていることから $f(0)$ は極小値である．
　ところが，$f(x)$ は $x=0$ の近くで $x^2$ と $3x^2$ の間を無限回振動するから，$f'(x)$ の符号は $x < 0$ 及び $x > 0$ それぞれで定符号ではない．

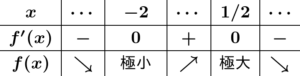
10.4 $\dfrac{f(x)}{g(x)}$ の極値

微分可能な関数 $\dfrac{f(x)}{g(x)}$ が，$x=a$ で極値をとるならば， \[ \frac{f(a)}{g(a)}=\frac{f'(a)}{g'(a)}\ \ \ \ (\mbox{ただし},g'(a)\neq 0)\]

証明

　$h(x)=\dfrac{f(x)}{g(x)}$ とおくと， \[h'(a)=\frac{f'(a)g(a)-f(a)g'(a)}{\{g(a)\}^2}=0\] であるから， \[\frac{f(a)}{g(a)}=\frac{f'(a)}{g'(a)}\]

■

例題　$f(x)=\dfrac{4x+3}{x^2+1}$ の極値を求めよ．

こたえ

　解答例を表示する

このページで疑問は解決されましたか？

　こちら から数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]