11. 関数のグラフ(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅲ　第2章　微分法

	スライド	ノート	問題
1. 微分係数と導関数	[無料]
2. 合成関数の導関数	[無料]
3. 逆関数の微分法	[無料]		[会員]
4. 三角関数の導関数	[会員]
5. 対数関数・指数関数の導関数	[会員]
6. 媒介変数表示と導関数	[会員]
7. 陰関数の導関数	[会員]
8. 平均値の定理	[会員]
9. 関数の値の変化	[会員]		[会員]
10. 関数の極大・極小	[会員]
11. 関数のグラフ	[会員]

11．関数のグラフ

11.1 曲線の凹凸

　微分可能な関数のグラフを考える．
　ある区間で，接線の傾きが増加しているとき，グラフはその区間で下に凸という．逆にその区間で接線の傾きが減少しているとき，グラフはその区間で上に凸という．

　例えばある区間で，$f'(x)$ の導関数である $f^{\prime\prime}(x)$ が常に正ならば，$f'(x)$ は単調に増加するから，$f(x)$ の接線の傾きは増加していく．即ち，その区間でグラフは下に凸である．ある区間で常に $f^{\prime\prime}(x) < 0$ となる場合も同様である．

まとめ　関数 $f(x)$ が $f^{\prime\prime}(x)$ をもつとき，
　　常に $f^{\prime\prime}(x)\!>\!0$ である区間でグラフは下に凸である．
　　常に $f^{\prime\prime}(x)<\!0$ である区間でグラフは上に凸である．

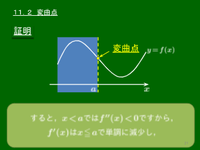
11.2 変曲点

　曲線の凹凸の境目を変曲点という．

変曲点であるための必要条件

　第2次導関数 $f^{\prime\prime}(x)$ をもつ関数 $f(x)$ について，グラフが $x=a$ を含むある区間において，$x=a$ で上に凸から下に凸に変わるとする．

　その区間内の $x<a$ で $f^{\prime\prime}(x) < 0$，$x > a$ で $f^{\prime\prime}(x) > 0$ だから，$f^{\prime\prime}(x)$ が連続ならば $f^{\prime\prime}(a)=0$
　$x=a$ で下に凸から上に凸に変わる場合も，同様の理由で $f^{\prime\prime}(a)=0$ となる．

定理　関数 $f(x)$ の第2次導関数 $f^{\prime\prime}(x)$ が連続のとき， $$\mbox{点}(a,\ f(a))\mbox{が変曲点}\ \ \Longrightarrow \ f^{\prime\prime}(a)=0$$

注意

　逆 $(\Leftarrow)$ はいえない．
(反例)
　$f(x)=x^4$ について，$f'(x)=4x^3$，$f^{\prime\prime}(x)=12x^2$ であるから，$f^{\prime\prime}(0)=0$．しかし，点$(0,f(0))$ は変曲点ではない．

11.3 漸近線の求め方

関数 $y=f(x)$ のグラフにおいて，

① $\displaystyle\lim_{x\to\infty}f(x)=a$，または$\displaystyle\lim_{x\to-\infty}f(x)=a$

　　→　直線 $y=a$ は漸近線．

② $\displaystyle\lim_{x\to a+0}f(x)=\infty$，又は$\displaystyle\lim_{x\to a+0}f(x)=-\infty$
又は$\displaystyle\lim_{x\to a-0}f(x)=\infty$，又は$\displaystyle\lim_{x\to a-0}f(x)=-\infty$

　　→　直線 $x=a$ は漸近線．

③ $\displaystyle\lim_{x\to\infty}\{f(x)-(ax+b)\}=0$，又は$\displaystyle\lim_{x\to-\infty}\{f(x)-(ax+b)\}=0$

　　→　直線 $y=ax+b$ は漸近線．

補足

③について，$y=ax+b$ の $a$ と $b$ はどのようにしてわかるか？

　もし，$f(x)$ のグラフが $x\to\infty$ で直線 $y=ax+b$ に漸近するならば，次が成り立つ：

$$a=\lim_{x\to\infty}\frac{f(x)}x,\ \ \ \ b=\lim_{x\to\infty}\{f(x)-ax\}$$

証明

　$\displaystyle\lim_{x\to\infty}\{f(x)-(ax+b)\}=0\ \cdots$① のとき， $$\lim_{x\to\infty}\frac{f(x)-(ax+b)}x=0$$ $$\therefore\lim_{x\to\infty}\left\{\frac{f(x)}x-a-\frac bx\right\}=0$$ $$\therefore \lim_{x\to\infty}\left\{\frac{f(x)}x-a\right\}=0\ \ (\because \frac bx\to0(x\to\infty))$$ $$\therefore a=\lim_{x\to\infty}\frac{f(x)}x$$ 　このようにして $a$ が求まれば，①により， $$\lim_{x\to\infty}\{f(x)-ax\}-b=0$$ $$\therefore b=\lim_{x\to\infty}\{f(x)-ax\}$$

■

補足

　$x\to-\infty$ のとき直線 $y=ax+b$ に漸近する場合も同様にして $a$ と $b$ を求めることができる．

注意

　$\displaystyle{a=\lim_{x\to\infty}\frac{f(x)}x}$ となる $a$ が存在しても，漸近線が存在するとは限らない．例えば $f(x)=x+\sqrt x$ のとき

$$\frac{f(x)}x=1+\frac1{\sqrt x}\to1\ \ (x\to\infty)$$

となるから $a=1$．然るに

$$\lim_{x\to\infty}\{f(x)-x\}=\lim_{x\to\infty}\sqrt x=\infty$$

となるから，$\displaystyle b=\lim_{x\to\infty}\{f(x)-ax\}$ は有限確定値とならない．別の例として $f(x)=\sin x$ とすれば，はさみうちの原理により $\dfrac {\sin x}x\to 0\ (x\to\infty)$ だが，サインカーブに漸近線はない．

　要するに $x\to\infty$ の場合では

曲線 $y=f(x)$ が直線 $y=ax+b$ を漸近線にもつ
$\iff \displaystyle\lim_{x\to\infty}\{f(x)-(ax+b)\}=0$
$\iff \displaystyle\lim_{x\to\infty}\{f(x)-ax\}=b$
$\color{red}{\Longrightarrow }\displaystyle\lim_{x\to\infty}\frac{f(x)}x=a$
※最後は矢印が右向きだけであることに注意

なのであって，$\displaystyle\lim_{x\to\infty}\{f(x)-ax\}=b$ (有限確定値) が成り立って初めて直線 $y=ax+b$ が漸近線であるといえる訳である．

例題　$f(x)=\dfrac{x^2}{x-1}$ の漸近線を求めよ．

答

　解答例を表示する

　まず，$x\to1+0$ のとき，$f(x)\to\infty$ により，直線 $x=1$ は漸近線．
（ $x\to1\!-\!0$ のとき，$f(x)\to-\infty$ となり，こちらから述べるのでもよい．）
　次に， $$\lim_{x\to\infty}\frac{f(x)}x=\lim_{x\to\infty}\frac x{x-1}=\lim_{x\to\infty}\frac1{1-\frac1x}=1,$$ $$\begin{align*} \lim_{x\to\infty}\{f(x)-1x\}&=\lim_{x\to\infty}\frac{x^2-x(x-1)}{x-1}\\[5pt] &=\lim_{x\to\infty}\frac x{x-1}\\[5pt] &=\lim_{x\to\infty}\frac1{1-\frac1x}\\[5pt] &=1 \end{align*}$$ であるから，直線 $y=x+1$ は漸近線．



別解

　グラフが漸近線をもつ仮分数式では，(整式)＋(真分数式) に変形すると，漸近線が自然と出現する．

　$f(x)=\dfrac{x^2}{x-1}=x+1+\dfrac 1{x-1}$ であるから

$$\lim_{x\to\infty}\{f(x)-(x+1)\}=\lim_{x\to\infty}\dfrac 1{x-1}=0$$

　よって直線 $y=x+1$ は漸近線である．

11.4 第2次導関数と極値

　$x=a$ を含むある区間で，$f^{\prime\prime}(x)$ が連続のとき，
[1] $f^\prime(a)=0$ かつ $f^{\prime\prime}(a)<0$ ならば，$f(a)$ は極大値
[2] $f^\prime(a)=0$ かつ $f^{\prime\prime}(a)>0$ ならば，$f(a)$ は極小値

証明

[1]の証明

　$f^{\prime\prime}(x)$ は連続だから，$f^{\prime\prime}(a) < 0$ ならば，$x=a$ の十分近くでは常に $f^{\prime\prime}(x) < 0$ となる．

　$f'(x)$ の導関数 $f^{\prime\prime}(x)$ が常に$f^{\prime\prime}(x) < 0$ となるから，$x=a$ の十分近くで $f'(x)$ は単調に減少する．$f'(a)=0$ だから，$f'(x)$ の符号は，$x=a$ の前後で正から負に転じる．

　即ち，$f(a)$ は極大値である．

（[2]も同様に証明される．）

■

---

高校数学[総目次]

数学Ⅲ　第2章　微分法

	スライド	ノート	問題
1. 微分係数と導関数	[無料]
2. 合成関数の導関数	[無料]
3. 逆関数の微分法	[無料]		[会員]
4. 三角関数の導関数	[会員]
5. 対数関数・指数関数の導関数	[会員]
6. 媒介変数表示と導関数	[会員]
7. 陰関数の導関数	[会員]
8. 平均値の定理	[会員]
9. 関数の値の変化	[会員]		[会員]
10. 関数の極大・極小	[会員]
11. 関数のグラフ	[会員]