3. 逆関数の微分法(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅲ　第2章　微分法

	スライド	ノート
1. 微分係数と導関数	[無料]
2. 合成関数の導関数	[無料]
3. 逆関数の微分法	[無料]
4. 三角関数の導関数	[会員]
5. 対数関数・指数関数の導関数	[会員]
6. 媒介変数表示と導関数	[会員]
7. 陰関数の導関数	[会員]
8. 平均値の定理	[会員]
9. 関数の値の変化	[会員]
10. 関数の極大・極小	[会員]
11. 関数のグラフ	[会員]

3．逆関数の微分法

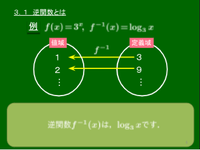
3.1 逆関数とは

　逆関数を論じる前に，「逆」の文字のない通常の「関数」とは何であったかを確認しておく．

　例として $y=x+1$ を考える．この式から，

　　$x=0$ のとき，$y=1$
　　$x=1$ のとき，$y=2$
　　$x=2$ のとき，$y=3$
　　　　　　$\vdots$

のように，$x$ の値に対して $y$ の値がただ1つ対応しているから $y$ は $x$ の関数であるといえる．

　いま $x$ の方を先に決めて，それに応じて $y$ の値が1つ決まったが，逆に $y$ の方を先に決めてもそれに応じて $x$ の値がただ1つ決まる：

　　$y=1$ のとき，$x=0$
　　$y=2$ のとき，$x=1$
　　$y=3$ のとき，$x=2$
　　　　　　$\vdots$

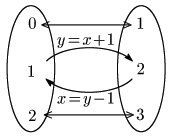
　つまり， $x$ は $y$ の関数となっているのである．この逆対応は $x=y-1$ である．数学においてはしばしば先に決める方の文字を $x$，それに伴って決まる方の文字を $y$ とおくので，この逆対応を表す関数は $x$ と $y$ の文字を入れ替えて

\[x=y-1\ \ \to\ \ y=x-1\]

と表される．この関数 $y=x-1$ をもとの関数 $y=x+1$ の逆関数という．

　上の例では $f(x)=x+1$ とすると，$f^{-1}(x)=x-1$ である．

　注意点として，ある関数に対してその逆関数は常に存在するとは限らない．例えば， 関数 $y=x^2$ は $x=2$ に対して $y=4$ が対応するが，逆に $y=4$ のとき， $x$ は $2$ と $-2$ の2つが対応しているため関数とは言えない．つまり関数 $y=x^2$ の逆関数は存在しない．

3.2 逆関数の微分法

　関数 $y=f(x)$ に逆関数があるとする．目標はこの関数の導関数 $\dfrac{dy}{dx}$ を求めるのに，逆関数の導関数を利用することである．

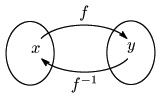
\[y=f(x)\iff x=f^{-1}(y)\ \cdots\mbox{①}\]

　この両辺を $x$ で微分すると， \[1=\frac d{dx}f^{-1}(y)\ \cdots\mbox{②}\] 　合成関数の導関数により， \[\begin{align*} \mbox{②の右辺}&=\frac d{dy}f^{-1}(y)\cdot\frac{dy}{dx}\\ &=\frac{dx}{dy}\cdot\frac{dy}{dx}\ \ (\because\mbox{①}) \end{align*}\] 　よって，②は \[\begin{gather*} 1=\frac{dx}{dy}\cdot\frac{dy}{dx}\\ \therefore\frac{dy}{dx}=\frac1{\frac{dx}{dy}} \end{gather*}\]

例題　$x>0$ とする．$y=x^{\frac1n}\ (\,n$ は自然数)のとき，$\dfrac{dy}{dx}$ を求めよ．

こたえ

　解答例を表示する >

　$y=x^{\frac1n}$ より $x=y^n$　$\therefore\dfrac{dx}{dy}=ny^{n-1}$
　よって， \[\begin{align*} \frac{dy}{dx}&=\frac1{\frac{dx}{dy}}=\frac1{ny^{n-1}}=\frac1ny^{1-n}\\ &=\frac1n\left(x^{\frac1n}\right)^{1-n}=\underline{\frac1nx^{\frac1n-1}} \end{align*}\]

　この例題の結果を用いて，以下の公式が示される：

公式　$r$ が有理数のとき， \[ (x^r)’=rx^{r-1} \]

証明

　$r=\dfrac mn\ (\,m$ は整数，$n$ は自然数)とおくと， \[y=x^{\frac mn}=\left(x^{\frac1n}\right)^m\] 　よって合成関数の導関数により， \[\begin{align*} \frac{dy}{dx}&=m\left(x^{\frac1n}\right)^{m-1}\cdot\left(x^{\frac1n}\right)’\\ &=mx^{\frac mn-\frac1n}\cdot \underline{\frac1n x^{\frac 1n-1}}\ \ (\because\mbox{上の例題})\\ &=\frac mn x^{\frac mn-1}\\ &=rx^{r-1} \end{align*}\]

■

例題1　$y=\sqrt[3]{x^4}$ を微分せよ．

こたえ

　解答例を表示する >

　$y=x^{\frac43}$ と表されるから，

\[y’=\frac43x^{\frac43-1}=\frac43x^{\frac13}=\underline{\frac43\sqrt[3]x}\]

例題2　$y=\sqrt[4]{x^2+x+1}$ を微分せよ．

こたえ

　解答例を表示する >

　$y=(x^2+x+1)^{\frac14}$ と表されるから，

\[y’=\frac14(x^2+x+1)^{-\frac34}\cdot(2x+1)=\underline{\frac{2x+1}{4\sqrt[4]{(x^2+x+1)^3}}}\]

応用例題　$y=\sin x\ (-\dfrac\pi2<x<\dfrac\pi2)$ の逆関数を $g(x)$ とするとき，$g'(x)$ を $x$ で表せ．

こたえ

　解答例を表示する >

　$y=\sin x$ より $x=\sin y\ (-1<x<1)$．よって，逆関数の微分法により，

\[\begin{align} \frac{dy}{dx}&=\frac 1{\frac{dx}{dy}}\\[5pt] &=\frac1{\cos y} \end{align}\]

　ここで，$-\dfrac\pi2<y<\dfrac\pi2$ のとき，$\cos y>0$ であるから，

\[\begin{align} \frac{dy}{dx}&=\frac 1{\sqrt{1-\sin^2y}}\\[5pt] &=\frac1{\sqrt{1-x^2}} \end{align}\]

\[\therefore \underline{\boldsymbol{ g'(x)=\frac1{\sqrt{1-x^2}}}}\]

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

---

高校数学[総目次]

数学Ⅲ　第2章　微分法

	スライド	ノート
1. 微分係数と導関数	[無料]
2. 合成関数の導関数	[無料]
3. 逆関数の微分法	[無料]
4. 三角関数の導関数	[会員]
5. 対数関数・指数関数の導関数	[会員]
6. 媒介変数表示と導関数	[会員]
7. 陰関数の導関数	[会員]
8. 平均値の定理	[会員]
9. 関数の値の変化	[会員]
10. 関数の極大・極小	[会員]
11. 関数のグラフ	[会員]