高校数学[総目次]
数学A 第1章 場合の数
| スライド | ノート | |
| 1. 集合 | [無料] | |
| 2. 場合の数 | [無料] | |
| 3. 順列 | [会員] | |
| 4. 円順列・重複順列 | [会員] | |
| 5. 組合せ | [会員] | |
| 6. 二項定理 | [会員] |

2.場合の数

2.1 樹形図
これからしばらくの間「…である場合は何通りか?」といった問いを考えていくことになるが,見つけた端から「1通り,2通り,3通り,…」と数えていくと,数え漏らしてしまったり,重複して数えてしまったりして,正しい答えが得られないということが起こり得る.場合の数を考える上では
漏れなく,ダブりなく
が何にも増しても重要であり,これを実現するために様々なアイデアが考案されている.その1つで最重要といえるのが次に紹介する樹形図である.
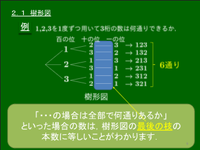
例題 1,2,3を1度ずつ用いて3桁の数は何通りできるか.
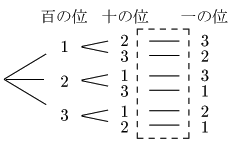
図より,6通り…(答)
上のような図を樹形図という.樹形図を見れば,「漏れなく,ダブりなく」がひと目で確認でき,題意の数が確かに6通りであるとわかる.このように樹形図は極めて優秀なツールと言える.樹形図によれば「…の場合は全部で何通りあるか」の答えが最後の枝(破線で囲まれた部分)の本数に示されている.ここでは最後の枝が6本であるから求めるものは6通りである.
樹形図の弱点
樹形図を描けば,どんなに複雑な設定でも機械的に正しく答えが得られるから極めて優秀なツールであることは間違いない.だがしかし,求める答えが最後の枝の本数であるという性格上,場合の数がちょっと大きくなるとたちまち木の枝が広がり,紙の上に書きつくすのに相等難儀する.このため,樹形図以外のアイデアも必要になってくるのである.

2.2 和の法則
例 さいころを1回だけ投げる場合
事柄A:2以下の目が出る.→1と2の2通り.
事柄B:4以上の目が出る.→4,5,6の3通り.
AまたはBが起こるのは,1,2,4,5,6 の5通りである.
ところで,AとBは同時には起こらない.(さいころを1回投げたとき,2以下の目が出て,かつ4以上の目も出る,つまり,2つの目が同時に出るということはない.)
このとき,AまたはBが起こる場合は, \[2+3=5(\mbox{通り})\] という具合に計算できる.
一般に次が成り立つ:
和の法則 事柄 A, B は同時に起こらないとする. A の起こり方が $m$ 通り,B の起こり方が $n$ 通りあるとき,A または B の起こる場合は\[m+n\ \mbox{通り}\]
注意
「同時に起こらない」という仮定は重要である.例えば,
事柄A:2以下の目が出る → 1と2の2通り
事柄B:偶数の目が出る → 2,4,6の3通り
とする.
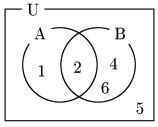
このとき,AまたはBが起こる場合は,
✕ $2+3=5$
○ $2+3-1=4$

2.3 積の法則
例 大小2つのさいころを同時に1回投げる.
事柄A:さいころ(大)の目が3以下→1,2,3の3通り
事柄B:さいころ(小)の目が5以上→5,6の2通り
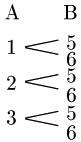
AとBがともに起こる場合は,右の樹形図より6通り.
ところで,Aが起こるどの場合でも,Bの起こる場合は5か6の2通りである.
このときAとBがともに起こる場合は, \[3\times2=6(\mbox{通り})\] といった具合に計算できる.
一般に次が成り立つ:
積の法則 事柄 A が起こる場合が $m$ 通り,その各々の場合に事柄 B が起こる場合が $n$ 通りあるとき,A と B がともに起こる場合は,\[mn\ \mbox{通り}\]

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学A 第1章 場合の数
| スライド | ノート | |
| 1. 集合 | [無料] | |
| 2. 場合の数 | [無料] | |
| 3. 順列 | [会員] | |
| 4. 円順列・重複順列 | [会員] | |
| 5. 組合せ | [会員] | |
| 6. 二項定理 | [会員] |