6. 二項定理(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学A　第1章　場合の数

	スライド	ノート	問題
1. 集合	[無料]
2. 場合の数	[無料]
3. 順列	[会員]		[会員]
4. 円順列・重複順列	[会員]
5. 組合せ	[会員]		[会員]
6. 二項定理	[会員]

6．二項定理

6.1　二項定理

　例として，$(a+b)^3$ を展開することを考える：

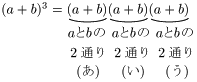
　この式を1つ1つ展開していく過程を考えると，(あ)から $a$ か $b$ のどちらかを選び，(い)から $a$ か $b$ のどちらかを選び，(う)から $a$ か $b$ のどちらかを選んで，それら3つを掛けると1つの項が得られる：

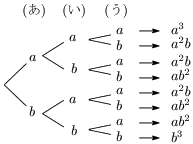
　得られた項は， $a^3$，$a^2b$，$ab^2$，$b^3$ の4種類であるが，それらがそれぞれ何個ずつあるかは次のような計算によって求めることができる：

$a^3$：(あ)～(う) の3つのグループから全て $a$ を選ぶと $a^3$ ができる．このとき $b$ は1つも選ばれないから，$b$ の選び方を考えて，

$_3{\rm C}_0=1$ 個

$a^2b$：(あ)～(う) のうち，2つのグループから $a$ を，1つのグループから $b$ の選べば $a^2b$ ができる．$b$ を(あ)～(う) のうち，どのグループから選ぶかを考えて，

$_3{\rm C}_1=3$ 個

$ab^2$：(あ)～(う) のうち，1つのグループから $a$ を，2つのグループから $b$ の選べば $ab^2$ ができる．$b$ を(あ)～(う) のうち，どの2つのグループから選ぶかを考えて，

$_3{\rm C}_2=3$ 個

$b^3$：(あ)～(う) の3つのグループ全てで $b$ を選べば $b^3$ ができる．従って，

$_3{\rm C}_3=1$ 個

　以上により，

$$(a+b)^3={_3{\rm C}_0}\,a^3+{_3{\rm C}_1}\,a^2b+{_3{\rm C}_2}\,ab^2+{_3{\rm C}_3}\,b^3$$

　一般に，二項定理と呼ばれる次の等式が成り立つ：

二項定理 $$\begin{align*}(a\!+\!b)^n\!=\!{_n{\rm C}_0}\, a^n+&{_n{\rm C}_1}\, a^{n-1}b\!+\!{_n{\rm C}_2}\, a^{n-2}b^2\!+\!\cdots\\ &+\!{_n{\rm C}_r}\, a^{n-r}b^r\!+\!\cdots\!+\!{_n{\rm C}_n}\, b^n\end{align*}$$

補足

　二項定理で，$a=1,b=x$ とおくと， $$\begin{align*} (1+x)^n&={_n{\rm C}}_01^n\!+\!{_n{\rm C}}_1 1^{n-1}x^1\!+\!{_n{\rm C}}_2 1^{n-2}x^2\!+\!\cdots\!+\!{_n{\rm C}}_n1^0x^n\\[5pt] &={_n{\rm C}}_0+{_n{\rm C}}_1 x+{_n{\rm C}}_2 x^2+\cdots+{_n{\rm C}}_n x^n \end{align*}$$ 　ここで，$x=1$，または $x=-1$ とおくことで次を得る：

$$\begin{align*} [1]\ {_n\mbox{C}}_0+&{_n\mbox{C}}_1\!+{_n\mbox{C}}_2\!+\!\cdots\!+{_n\mbox{C}}_n\!=\!2^n\\[5pt] [2]\ {_n\mbox{C}}_0-&{_n\mbox{C}}_1\!+{_n\mbox{C}}_2\!-\!\cdots\\ &+\!(-1)^r{_n\mbox{C}}_r\!+\!\cdots\!+\!(-1)^n{_n\mbox{C}}_n\!\!=\!0 \end{align*}$$

6.2　パスカルの三角形

$$\begin{align*} (a+b)^1&=\hspace{17mm}1a+1b\\[5pt] (a+b)^2&=\hspace{10mm}1a^2+2ab+1b^2\\[5pt] (a+b)^3&=\hspace{4mm}1a^3+3a^2b+3ab^2+1b^3\\[5pt] (a+b)^4&=1a^4\!+\!4a^3b\!+\!6a^2b^2\!+\!4ab^3\!+\!1b^4\\[5pt] &\hspace{4mm}\vdots \end{align*}$$

　右辺について，係数だけを列挙すると，

1　1
1　2　1
1　3　3　1
1　4　6　4　1
1　5　10　10　5　1
1　6　15　20　15　6　1
$\vdots$

　これをパスカルの三角形という．この三角形は，

①　各行の両端は1である．
②　間の数は，すぐ上にある2数の和である．

という規則で上から順に下へと書き進めることができる．

補足

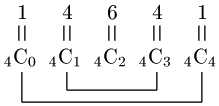
　$(a+b)^4$ の段を例にとると，次の関係が成り立っていることがわかる：

$$_n{\rm C}\,_r=\,_n{\rm C}\,_{n-r}$$

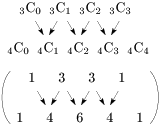
　$(a+b)^3$ と $(a+b)^4$ の段を例にとると，次の関係が成り立っていることがわかる：

$$_n{\rm C}\,_r=\,_{n-1}{\rm C}\,_{r-1}+\,_{n-1}{\rm C}\,_r$$

---

高校数学[総目次]

数学A　第1章　場合の数

	スライド	ノート	問題
1. 集合	[無料]
2. 場合の数	[無料]
3. 順列	[会員]		[会員]
4. 円順列・重複順列	[会員]
5. 組合せ	[会員]		[会員]
6. 二項定理	[会員]