高校数学[総目次]
数学A 第1章 場合の数
| スライド | ノート | |
| 1. 集合 | [無料] | |
| 2. 場合の数 | [無料] | |
| 3. 順列 | [会員] | |
| 4. 円順列・重複順列 | [会員] | |
| 5. 組合せ | [会員] | |
| 6. 二項定理 | [会員] |

5.組合せ
5.1 組合せ
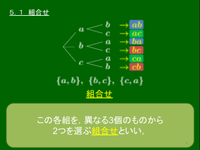
$a,b,c$ の3文字から2文字を選んで一列に並べる順列は,
の6通りがある.このうち
$ab$ と $ba$,$bc$ と $cb$,$ca$ と $ac$
は選んだ文字がそれぞれ同じになっている.選んだ2つを一列に並べたりしないで,どの2つが選ばれたかだけに興味をもつならこのような重複を考慮して
$\{a,b\}$,$\{b,c\}$,$\{c,a\}$
の3組だけとなる.この各組を,異なる3個のものから2個を選ぶ組合せといい,その総数を
\[_3{\rm C}_2\]
で記号化する.すなわち $_3{\rm C}_2=3$ である.
順列 $_3{\rm P}_2$ との関係は,上の各組において順番まで考慮したものが順列であり,この場合だと各組合せから $2\,!=2\times1=2$(通り)の順列ができるから,
\[\begin{align*} _3{\rm C}_2\times2\,!&=\,_3{\rm P}_2\\[5pt] \therefore\ _3{\rm C}_2&=\frac{_3{\rm P}_2}{2!}\left(=\frac{3\cdot2}{2\cdot1}=3\right) \end{align*}\]
一般に異なる $n$ 個のものから $r$ 個選ぶ組合せは,
$_n{\rm C}_r=\dfrac{_n{\rm P}_r}{r\,!}$ (通り)
である.更に,$_n{\rm P}_r=\dfrac{n\,!}{(n-r)\,!}$ であったから,
\[_n{\rm C}_r=\frac{n\,!}{(n-r)\,!\,r\,!}\]
とも書ける.
また,$_n{\rm C}_0=1$ と定める.
補足
「C」は英語で組合せを意味する ‘Combination’ の頭文字である.
組合せ 異なる $n$ 個のものから $r$ 個選ぶ組合せの総数は,\[_n\mbox{C}\,_r=\frac{_n\mbox{P}_r}{r\,!}=\frac{n\,!}{(n-r)\,!\,r\,!}\] 特に\[_n\mbox{C}\,_0=1\]

5.2 組合せの性質
\begin{align*} &[1]\ \ _n\mbox{C}\,_r={_n\mbox{C}}\,_{n-r}\\[5pt] &[2]\ \ _n\mbox{C}\,_r={_{n-1}\mbox{C}}\,_{r-1}+{_{n-1}\mbox{C}}\,_r\\[5pt] &[3]\ \ r\,_n\mbox{C}\,_r=n\,_{n-1}\mbox{C}\,_{r-1} \end{align*}
証明
[1] (左辺) $=\dfrac{n!}{(n-r)!\,r!}$
(右辺) $=\dfrac{n!}{\{n-(n-r)\}!\,(n-r)!}=\dfrac{n!}{r!\,(n-r)!}$
よって,(左辺) $=$ (右辺)
[2]
\[\begin{align*}
(\mbox{右辺})&=\frac{(n-1)!}{\{(n\!-\!1)\!-\!(r\!-\!1)\}!\,(r\!-\!1)!}\!+\!\frac{(n-1)!}{\{(n\!-\!1)\!-\!r\}!\,r!}\\[5pt]
&=\frac{(n-1)!}{(n-r)!\,(r-1)!}+\frac{(n-1)!}{(n-r-1)!\,r!}\\[5pt]
&=\frac{(n-1)!\{r+(n-r)\}}{(n-r)!\,r!}\ (\gets\mbox{通分して計算})\\[5pt]
&=\frac{(n-1)!\times n}{(n-r)!\,r!}\\[5pt]
&=\frac{n!}{(n-r)!\,r!}\\[5pt]
&=(\mbox{左辺})
\end{align*}\]
[3]
\[\begin{align*}
(\mbox{左辺})&=r\cdot\frac{n!}{(n-r)!\,r!}\\[5pt]
&=n\cdot\frac{(n-1)!}{(n-r)!\,(r-1)!}\\[5pt]
&=n\cdot\frac{(n-1)!}{\{(n\!-\!1)\!-\!(r\!-\!1)\}!\,(r\!-\!1)!}\\[5pt]
&=(\mbox{右辺})
\end{align*}\]
■
補足
上の性質は,次のように考えると理解しやすい.
[1] $n$ 人から $r$ 人の掃除当番を決めるのに,掃除当番でない $n-r$ 人を決めれば,残りが自動的に掃除当番となる.
[2] パスカルの三角形
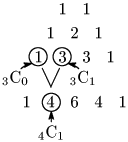
\[_4{\rm C}_1=\,_3{\rm C}_0+\,_3{\rm C}_1\]
[3]
$r\,_n{\rm C}_r$:$n$ 人から $r$ 人のグループを作り,更にその中からボスを選ぶ.
$n\,_{n-1}{\rm C}_{r-1}$:まずボスを決めて,残りの $n-1$ 人からグループに入る $r-1$ 人を選ぶ.

5.3 同じものを含む順列
例題 1,1,2の3つの数を使って3桁の数は何通りできるか.
2つある1を,$1_a$,$1_b$ と区別する:
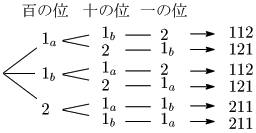
全6通りのうち,2つ$(=2!)$ ずつ同じものがあるから,
$\dfrac{3!}{2!}=\dfrac{3\cdot2\cdot1}{2\cdot1}=3$ 通り
$n$ 個のうち,$p$ 個の同じもの,$q$ 個の同じもの,$r$ 個の同じものがあり,これらを1列に並べる場合が何通りあるかを考える.まずはどんなに同じに見えるものでも区別して順列を考えると $n!$ 通り.このうち,$p!$ 通りの区別のできないものが含まれる,即ち $n!$ 通りの中には $p!$ 重カウントされているものがあるから $p!$ で割る.同様に $q!$ 重カウント,$r!$ 重カウントになっているものがあるからそれらを割る.
一般に次が成り立つ:
重複順列
$n$ 個のうち,$p$ 個の同じもの,$q$ 個の同じもの,$r$ 個の同じものがるとき,これらを1列に並べる方法は,\[\frac{n!}{p!\,q!\,r!} \ \ \mbox{通り}\]

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
演習問題
1 6人をX,Y,Zの3つのグループに2人ずつ分ける方法は何通りあるか.
2 6人を2人ずつ3つのグループに分ける方法は何通りあるか.
ヒント 問題1との違いに注意が必要です.
3 AからBに最短で行く方法は何通りあるか.
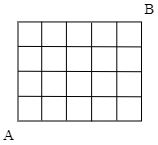
ヒント 計算一発で求める方法とコツコツ書き込む方法があります.
4 $x,y,z$ は0以上の整数とする.$x+y+z=10$ となる $(x,y,z)$ の組は何通りあるか.
ヒント 計算一発で求める上手い方法があります.
5 $x,y,z$ は整数とする.$x+y+z=10$,$x\geqq 2$,$y\geqq1$,$z\geqq0$ となる $(x,y,z)$ の組は何通りあるか.
ヒント 問題4に制限が付きましたが,ちょっと工夫するだけで問題4と同じ設定に帰着できます.
6 $x,y,z$ は0以上の整数とする.$x+y+z=10$,$x\leqq 5$,$y\leqq5$,$z\leqq5$ となる $(x,y,z)$ の組は何通りあるか.
ヒント 「以下」は「以上」よりずっと状況が複雑です.でも発想の転換で実はこれも問題4と同じ設定に帰着できます.
7 $x,y,z$ は整数とする.$1\leqq x<y<z\leqq10$ となる $(x,y,z)$ の組は何通りあるか.
ヒント $x,y,z$ には大小関係があるので順列の問題かと思いきや,実は組合せの問題です.
8 $x,y,z$ は整数とする.$1\leqq x\leqq y\leqq z\leqq10$ となる $(x,y,z)$ の組は何通りあるか.
ヒント 問題7との違いに注意してください.ちょっとした工夫で計算一発で解決です.
9 $x,y,z$ は自然数とする.$x+y+z\leqq10$ となる $(x,y,z)$ の組は何通りあるか.
ヒント 計算一発で解決する工夫を考えてみてください.
解答
1 6人をX,Y,Zの3つのグループに2人ずつ分ける方法は何通りあるか.
X,Y,Zのどのグループから決めても問題はありません.
こたえ
Xの選び方が
$_6{\rm C}_2=\dfrac{6\cdot5}{2\cdot1}=15$(通り)
その各々に対してYの選び方が