順列・階乗

このページにある内容は，こちらのスライド でわかり易く説明しています．

PC環境なら全画面表示でより見やすく，よりわかりやすい！
全画面表示の仕方は こちら

数学A　第1章　場合の数

	スライド	ノート	問題
1. 集合
2. 場合の数
3. 順列
4. 円順列・重複順列
5. 組合せ
6. 二項定理

3．順列

3.1　順列

　異なる $𝑛$ 個のものから $𝑟$ 個選び，それらを1列に並べる順列の総数は，

　先頭の選び方が $𝑛$ 通り
　2番目の選び方が $(𝑛 - 1)$ 通り
　3番目の選び方が $(𝑛 - 2)$ 通り
　　 $⋮$
　 $𝑟$ 番目の選び方が $(𝑛 - 𝑟 + 1)$ 通り

となるから，

$𝑛 \times (𝑛 - 1) \times (𝑛 - 2) \times \dots \times (𝑛 - 𝑟 + 1)$ 通り

である．この式を

$𝑛 P 𝑟$

と記号化する：

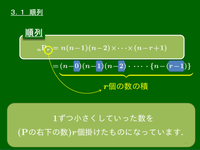
順列 $𝑛 P 𝑟 = 𝑛 (𝑛 - 1) (𝑛 - 2) \times \dots \times (𝑛 - 𝑟 + 1)$

補足

「P」は英語で順列を意味する Permutation の頭文字である．

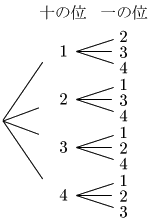
例題　1,2,3,4から異なる2つを選んで1列に並べる方法は何通りあるか．

こたえ

$4 P 2 = 4 \times 3 = 12$ 通り

補足

　樹形図を見れば，求める順列の総数を $4 \times 3$ で数えられることがよくわかる．すなわち最初の枝が4本，そのどの枝からも3本ずつ枝が出ているから，最後の枝は12本ある．

3.2　階乗

　 $𝑛 P 𝑟$ において，特に $𝑟 = 𝑛$ のとき，すなわち異なる $𝑛$ 個のものを1列に並べる順列の総数は， $𝑛 P 𝑛 = 𝑛 \times (𝑛 - 1) \times (𝑛 - 2) \times \dots \times 2 \times 1$ である．右辺を $𝒏$ の階乗といい， $𝑛!$ で表す．また， $𝑛 = 0$ の場合は特別に $0! = 1$ と定める(定義する)．

階乗 $𝑛! = 𝑛 (𝑛 - 1) (𝑛 - 2) \times \dots \times 2 \cdot 1$ 　　特に， $0! = 1$

例題　1,2,3 の3つの数を1列に並べて得られる3桁の数は何個あるか．

こたえ

$3! = 3 \times 2 \times 1 = 6$ 個

補足

　最初の枝が3本，そのそれぞれから2本ずつ，そして更にその枝から1本ずつ出ている．

$𝑛$ P $𝑟$ を階乗で表す

$𝑛 P 𝑟 = 𝑛 (𝑛 - 1) \times \dots \times (𝑛 - 𝑟 + 1) = 𝑛 (𝑛 - 1) \times \dots \times (𝑛 - 𝑟 + 1) \cdot (𝒏 - 𝒓) \times \dots \times 𝟐 \times 𝟏 (𝒏 - 𝒓) \times \dots \times 𝟐 \times 𝟏 = 𝑛! (𝑛 - 𝑟)!$ $∴ 𝑛 P 𝑟 = 𝑛! (𝑛 - 𝑟)!$ 　この式が $𝑟 = 0$ でも成り立つように， $𝑛 P 0 = 1$ と定める．

順列 $𝑛 P 𝑟 = 𝑛! (𝑛 - 𝑟)!$ 　　特に， $𝑛 P 0 = 1$

このページで疑問は解決されましたか？

　こちら から数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]

数学A　第1章　場合の数

	スライド	ノート	問題
1. 集合
2. 場合の数
3. 順列
4. 円順列・重複順列
5. 組合せ
6. 二項定理

順列・階乗

3．順列

3.1 順列

補足

補足

3.2 階乗

補足

𝑛P𝑟 を階乗で表す

3.1　順列

3.2　階乗

$𝑛$ P $𝑟$ を階乗で表す