3. 三角関数の性質(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅱ　第4章　三角関数

	スライド	ノート
1. 一般角と弧度法	[無料]
2. 一般角の三角関数	[無料]
3. 三角関数の性質	[無料]
4. 三角関数のグラフ	[会員]
5. 三角関数の加法定理	[会員]
6. 三角関数の種々の公式	[会員]
7. 三角関数の合成	[会員]
8. 三角関数の応用	[会員]

3.1　三角関数の相互関係

　一般角 $\theta$ に対しても，次の3つの最重要な関係式が成り立つ．

　任意の角$\theta$について，次が成り立つ：\begin{align*} &[1]\ \sin^2\theta+\cos^2\theta=1\\[5pt] &[2]\ \tan\theta=\frac{\sin\theta}{\cos\theta}\\ &[3]\ 1+\tan^2\theta=\frac1{\cos^2\theta} \end{align*}

例題　$\theta$ は第2象限の角とする．$\sin\theta=\dfrac23$ のとき，$\cos\theta$，及び $\tan\theta$ の値を求めよ．

　$\theta$ が第2象限の角 $\iff \cos\theta<0$，$\tan\theta<0$ であるから， \[\begin{align*} \cos\theta&=-\sqrt{1-\left(\frac23\right)^2}=\underline{\boldsymbol{-\frac{\sqrt5}3}}\\[5pt] \tan\theta&=\frac{\sin\theta}{\cos\theta}=\frac{\frac23}{-\frac{\sqrt5}3}=\underline{\boldsymbol{-\frac2{\sqrt5}}} \end{align*}\]

補足

　視覚的に考えることもできる．
　$\sin\theta=\dfrac23$
　　→　斜辺3，高さ2の直角三角形を第2象限に作る．
　　→　三平方の定理で底辺を求める．
　　　　(このとき，$-\sqrt5$ としておく．)

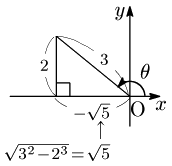
　図より， \[\begin{align*} \cos\theta&=\frac{-\sqrt5}3=-\frac{\sqrt5}3\\[5pt] \tan\theta&=\frac2{-\sqrt5}=-\frac2{\sqrt5} \end{align*}\]

3.2　三角関数の性質

\begin{align*}&[1]\left\{\begin{array}{l}\sin(\theta+2n\pi)=\sin\theta\\ \cos(\theta+2n\pi)=\cos\theta\ \ \ (n\mbox{は整数})\\ \tan(\theta+2n\pi)=\tan\theta\end{array} \right.\\\\ &[2]\left\{\begin{array}{l}\sin(-\theta)=-\sin\theta\\ \cos(-\theta)=\cos\theta\\ \tan(-\theta)=-\tan\theta\end{array} \right.\\\\ &[3]\left\{\begin{array}{l}\sin(\theta+\pi)=-\sin\theta\\ \cos(\theta+\pi)=-\cos\theta\\ \tan(\theta+\pi)=\tan\theta\end{array} \right.\\\\ &[4]\left\{\begin{array}{l}\sin\left(\theta+\dfrac\pi2\right)=\cos\theta\\ \cos\left(\theta+\dfrac\pi2\right)=-\sin\theta\\ \tan\left(\theta+\dfrac\pi 2\right)=-\dfrac 1{\tan\theta}\end{array} \right. \end{align*}

覚え方

(詳しくはスライドで．)

[ステップ1] sin, cos, tan を決める

　① 横軸に当たる($\cdots, -\pi, 0, \pi, 2\pi, \cdots$)
　　　→　変化なし
　② 縦軸に当たる　$(\cdots, -\dfrac\pi2, \dfrac\pi2, \dfrac32\pi, \cdots)$
　　　→　$\left\{\begin{array}{l} \sin\to\cos\\ \cos\to\sin\\ \tan\to\frac1{\tan} \end{array}\right.$

[ステップ2] 符号を決める

　$\theta$ を鋭角と仮定し，$\pi-\theta$，$\dfrac\pi2+\theta$ などが属する象限によって決める．

3.3　三角関数の特徴

[1] グラフの対称性

$\sin x,\ \tan x$ は奇関数　　　
　　　→　グラフは原点対称
$\cos x$ は偶関数　　　　　
　　　→　グラフは $y$ 軸対称

　　[補足]　任意の $x$ について， \[\begin{array}{ll} f(-x)=-f(x)&\to\ f(x)\ \mbox{は奇関数}\\[5pt] f(-x)=f(x)&\to\ f(x)\ \mbox{は偶関数} \end{array}\]

[2] 周期関数である

　　$\sin x,\ \cos x$　→　周期は $2\pi$
　　$\tan x$　　　　→　周期は $\pi$

　　[補足]　任意の $x$ について， \[f(x+p)=f(x)\ \ (p\neq0)\] 　　が成り立つとき，$f(x)$ を周期 $p$ の周期関数という．

---

高校数学[総目次]

数学Ⅱ　第4章　三角関数

	スライド	ノート
1. 一般角と弧度法	[無料]
2. 一般角の三角関数	[無料]
3. 三角関数の性質	[無料]
4. 三角関数のグラフ	[会員]
5. 三角関数の加法定理	[会員]
6. 三角関数の種々の公式	[会員]
7. 三角関数の合成	[会員]
8. 三角関数の応用	[会員]