高校数学[総目次]
数学Ⅱ 第4章 三角関数
| スライド | ノート | |
| 1. 一般角と弧度法 | [無料] | |
| 2. 一般角の三角関数 | [無料] | |
| 3. 三角関数の性質 | [無料] | |
| 4. 三角関数のグラフ | [会員] | |
| 5. 三角関数の加法定理 | [会員] | |
| 6. 三角関数の種々の公式 | [会員] | |
| 7. 三角関数の合成 | [会員] | |
| 8. 三角関数の応用 | [会員] |

4.1 $\sin\theta$ のグラフ
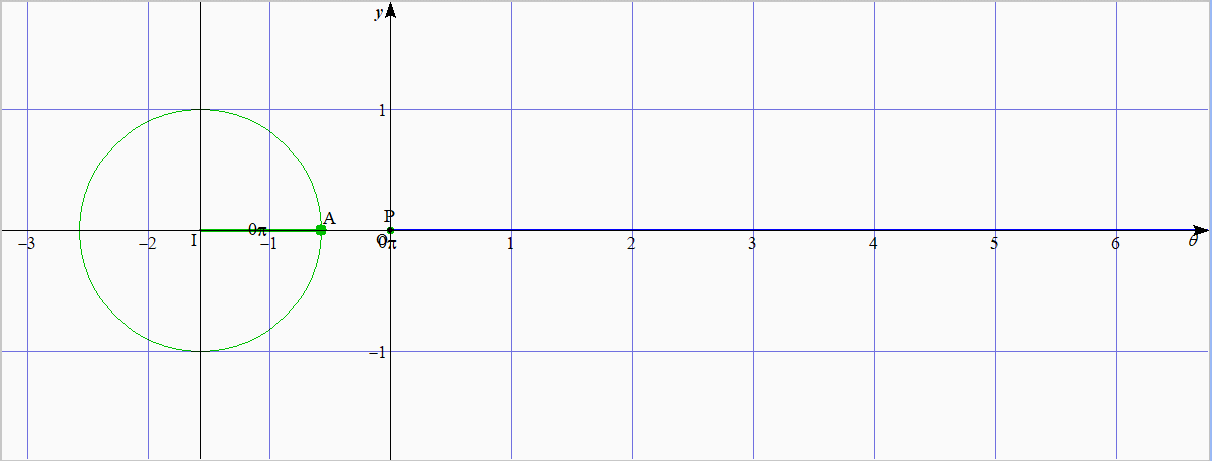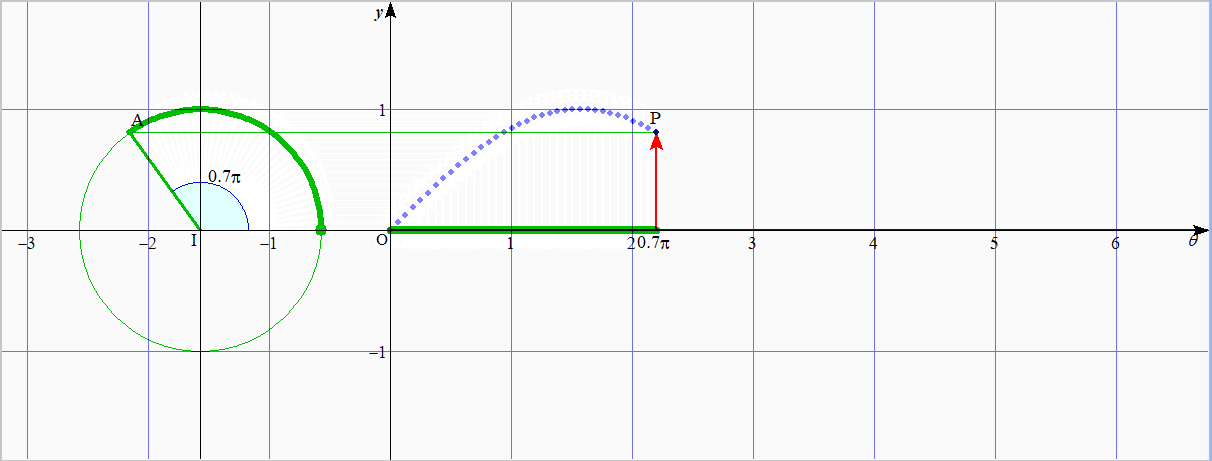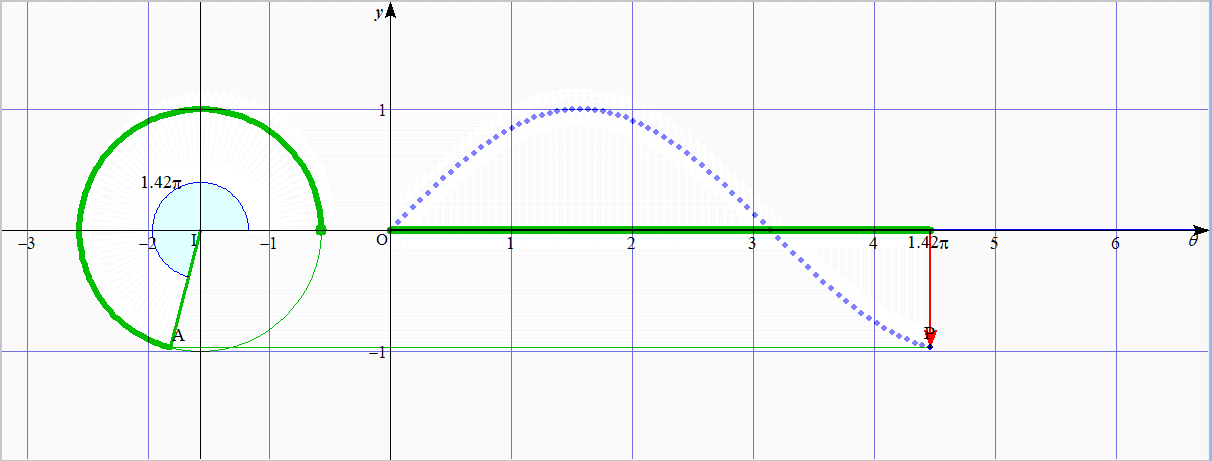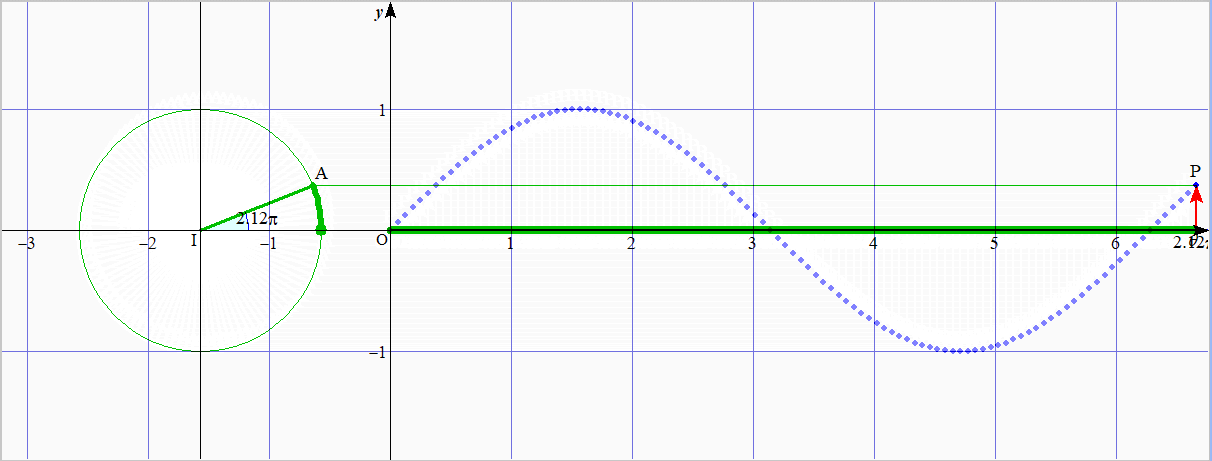
緑色の太線が同じ長さ
$y=\sin\theta$ のグラフのかき方は,スライド(会員向け)でもパラパラ漫画的にわかりやすく解説しています.
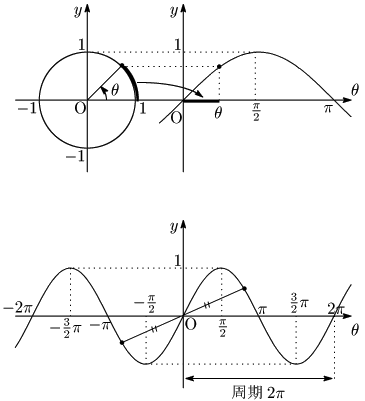
下:$y=\sin\theta$ のグラフ
グラフは原点対称

4.2 $\cos\theta$ のグラフ
$y=\cos\theta$ のグラフのかき方は,スライド(会員向け)でパラパラ漫画的にわかりやすく解説しています.
$y=\cos\theta=\sin\left(\theta+\dfrac\pi2\right)$ を利用
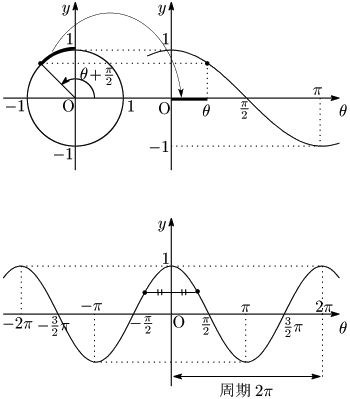
下:$y=\cos\theta$ のグラフ
グラフは $y$ 軸対称

4.3 $\tan\theta$ のグラフ
$y=\tan\theta$ のグラフのかき方は,スライド(会員向け)でパラパラ漫画的にわかりやすく解説しています.
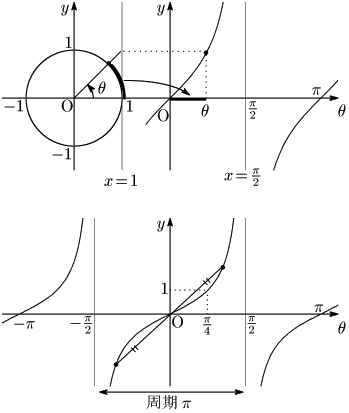
下:$y=\tan\theta$ のグラフ
グラフは原点対称
$n$ を整数として,直線 $y=\dfrac\pi2+n\pi$ が漸近線.

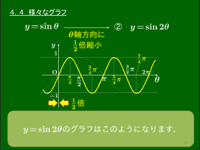
4.4 様々なグラフ
$y=\sin\theta$ のグラフからスタートして,
- $y=2\sin\theta$
- $y=\sin2\theta$
- $y=\sin\left(\theta-\dfrac\pi4\right)+1$
という変換によってグラフがどのように変化するのかを順に確認する.
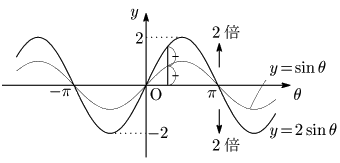
① $y$ 軸方向の拡大・縮小
$y=\sin\theta$ → $y=2\sin\theta$
($\boldsymbol{y}$ 軸方向に2倍拡大)
② $\theta$ 軸方向の拡大・縮小
$y=\sin\theta$ → $y=\sin2\theta$
($\theta$ 軸方向に $\boldsymbol{\dfrac12}$ 倍縮小)
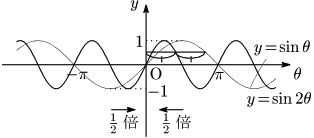
※この変換によって周期が変化する.
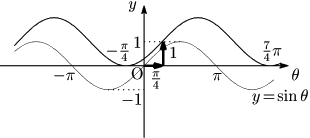
③ 平行移動
$y=\sin\theta$ → $y=\sin\left(\theta-\dfrac\pi4\right)+1$
($\boldsymbol{\theta}$ 軸方向に $\boldsymbol{\dfrac\pi4}$,$\boldsymbol{y}$ 軸方向に$1$だけ平行移動)
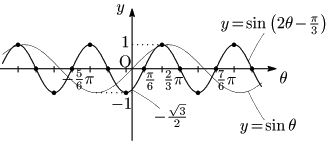
例題 $y=\sin\left(2\theta-\dfrac\pi3\right)$ のグラフをかけ.
考え方
$y=\sin\theta$ のグラフから始めて,どのような変換をたどって $y=\sin\left(2\theta-\dfrac\pi3\right)$ になったか考える.
考え方その1
$y=\sin2\left(\theta-\dfrac\pi6\right)$ と変形して,
$y$ 軸を中心に,$\theta$ 軸方向に $\dfrac12$ 倍の縮小($y=\sin2\theta$)
→ $\theta$ 軸方向に $\dfrac\pi6$ だけ平行移動($y=\sin2\left(\theta-\dfrac\pi6\right)$)
と考える.
考え方その2
$\theta$ 軸方向に $\dfrac\pi3$ だけ平行移動($y=\sin\left(\theta-\dfrac\pi3\right)$)
→ $y$ 軸を中心に,$\theta$ 軸方向に $\dfrac12$ 倍の縮小($y=\sin\left(2\theta-\dfrac\pi3\right)$)
と考える.
ポイント
グラフは
拡大・縮小 → 平行移動
の順で変換されたとするのが考えやすい.
この例題の場合も,考え方その1が考えやすい.グラフをかく際は,次に示すように考え方その1で捉えた平行移動量の情報から書き込んでいく:
グラフのかき方のコツ
ステップ1 平行移動量をとり,周期ごとに点を打つ.
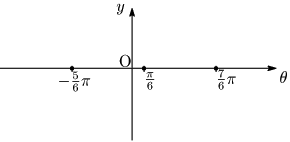
ステップ2 次々と間の点を取っていく.
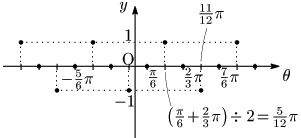
ステップ3 各点を滑らかに連結する.

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第4章 三角関数
| スライド | ノート | |
| 1. 一般角と弧度法 | [無料] | |
| 2. 一般角の三角関数 | [無料] | |
| 3. 三角関数の性質 | [無料] | |
| 4. 三角関数のグラフ | [会員] | |
| 5. 三角関数の加法定理 | [会員] | |
| 6. 三角関数の種々の公式 | [会員] | |
| 7. 三角関数の合成 | [会員] | |
| 8. 三角関数の応用 | [会員] |