5. 三角関数の加法定理(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅱ　第4章　三角関数

	スライド	ノート	問題
1. 一般角と弧度法	[会員]
2. 一般角の三角関数	[会員]
3. 三角関数の性質	[会員]		[会員]
4. 三角関数のグラフ	[会員]
5. 三角関数の加法定理	[会員]		[会員]
6. 三角関数の種々の公式	[会員]
7. 三角関数の合成	[会員]
8. 三角関数の応用	[会員]

5.1　sin, cos の加法定理

$$\begin{align*} &[1]\ \sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\\[5pt] &[2]\ \sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta\\[5pt] &[3]\ \cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\\[5pt] &[4]\ \cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta \end{align*}$$

証明

[4]

　P$(\cos\alpha,\sin\alpha)$，Q$(\cos\beta,\sin\beta)$ とおく．

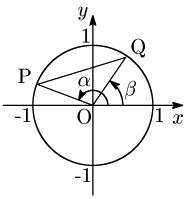
　距離の公式により， $$\begin{align*} {\rm PQ}^2&=(\cos\alpha-\cos\beta)^2+(\sin\alpha-\sin\beta)^2\\[5pt] &=2\{1-(\cos\alpha\cos\beta+\sin\alpha\sin\beta)\} \end{align*}$$

　ここで，P，Qを原点を中心に $-\beta$ だけ回転した点をそれぞれP$’$，Q$’$ とすると，${\rm P}'(\cos(\alpha-\beta ),\sin(\alpha-\beta))$，${\rm Q}'(1,0)$ となる：

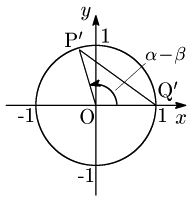
　再び距離の公式により， $$\begin{align*} {\rm P’Q’}^2&=\{\cos(\alpha-\beta)-1\}^2+\{\sin(\alpha-\beta)-0\}^2\\[5pt] &=2\{1-\cos(\alpha-\beta)\} \end{align*}$$ 　${\rm PQ^2=P’Q’^2}$ により， $$2\{1-(\cos\alpha\cos\beta+\sin\alpha\sin\beta)\}=2\{1-\cos(\alpha-\beta)\}$$ 　整理して $$\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$$

[3]

　[4] で $\beta$ を $-\beta$ におきかえると， $$\begin{align*} \cos\{\alpha-(-\beta)\}&=\cos\alpha\cos(-\beta)+\sin\alpha\sin(-\beta)\\[5pt] \therefore \cos(\alpha+\beta)&=\cos\alpha\cos\beta-\sin\alpha\sin\beta \end{align*}$$

[1]

　[3] で $\alpha$ を $\alpha+\dfrac\pi2$ におきかえると， $$\begin{align*} \cos\left\{\!\left(\!\alpha\!+\!\frac\pi2\right)\!+\!\beta\right\}\!&=\cos\left(\!\alpha\!+\!\frac\pi2\right)\!\cos\beta\!-\!\sin\left(\alpha\!+\!\frac\pi2\right)\!\sin\beta\\[5pt] \therefore -\sin(\alpha+\beta)&=-\sin\alpha\cos\beta-\cos\alpha\sin\beta\\[5pt] \therefore \sin(\alpha+\beta)&=\sin\alpha\cos\beta+\cos\alpha\sin\beta \end{align*}$$

[2]

　[1] で $\beta$ を $-\beta$ におきかえると， $$\begin{align*} \sin\{\alpha+(-\beta)\}&=\sin\alpha\cos(-\beta)+\cos\alpha\sin(-\beta)\\[5pt] \therefore \sin(\alpha-\beta)&=\sin\alpha\cos\beta-\cos\alpha\sin\beta \end{align*}$$

■

例

$$\begin{align*} \sin\frac7{12}\pi&=\sin\left(\frac\pi3+\frac\pi4\right)\\[5pt] &=\sin\frac\pi3\cos\frac\pi4+\cos\frac\pi3\sin\frac\pi4\\[5pt] &=\frac{\sqrt3}2\cdot\frac1{\sqrt2}+\frac12\cdot\frac1{\sqrt2}\\[5pt] &=\underline{\boldsymbol{\frac{\sqrt6+\sqrt2}4}} \end{align*}$$

$$\begin{align*} \cos\frac7{12}\pi&=\cos\left(\frac\pi3+\frac\pi4\right)\\[5pt] &=\cos\frac\pi3\cos\frac\pi4-\sin\frac\pi3\sin\frac\pi4\\[5pt] &=\frac12\cdot\frac1{\sqrt2}-\frac{\sqrt3}2\cdot\frac1{\sqrt2}\\[5pt] &=\underline{\boldsymbol{\frac{\sqrt2+\sqrt6}4}} \end{align*}$$

5.2　tan の加法定理

$$\begin{align*} &[1]\ \tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\\ &[2]\ \tan(\alpha-\beta)=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\\ \end{align*}$$

証明

$$\begin{align*} \tan(\alpha+\beta)&=\frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}\\[5pt] &=\frac{\sin\alpha\cos\beta+\cos\alpha\cos\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta}\\[5pt] &=\frac{\frac{\sin\alpha\cos\beta}{\cos\alpha\cos\beta}+\frac{\cos\alpha\sin\beta}{\cos\alpha\cos\beta}}{1-\frac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}}\\[5pt] &=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta} \end{align*}$$ 　$\beta$ を $-\beta$ におきかえると， $$\begin{align*} \tan\{\alpha+(-\beta)\}&=\frac{\tan\alpha+\tan(-\beta)}{1-\tan\alpha\tan(-\beta)}\\[5pt] \therefore \tan(\alpha-\beta)&=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \end{align*}$$

■

5.3　直線の傾きと tan

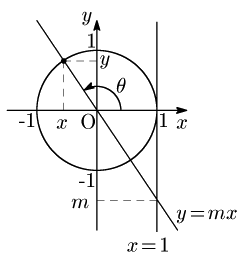
　直線 $y=mx$ と $x$ 軸の正の向きとのなす角を $\theta$ とすると，$\tan\theta$ の値は，「2.2 単位円における三角関数」で確認したように2直線 $y=mx$ と $x=1$ との交点の $y$ 座標として現れる：

$\tan\theta=m$
(ただし，$0\leqq\theta< \pi,\theta\neq\dfrac\pi2)$

　このとき，直線 $y=mx$ に平行である直線 $y=mx+n$ と $x$ 軸の正の向きとのなす角も $\theta$ であるから，一般に次が成り立つ：

直線の傾きとtan 　直線 $y=mx+n$ と $x$ 軸の正の向きとのなす角を $\theta$ とすると， $$\tan\theta=m$$ $$(\mbox{ただし，}0\leqq\theta< \pi,\theta\neq\dfrac\pi2)$$

5.4　2直線のなす鋭角

　2直線 $y\!=\!m_1x\!+\!n_1, \ y\!=\!m_2x\!+\!n_2$ のなす鋭角を $\theta$ とすると， $$\tan\theta=\left|\frac{m_1-m_2}{1+m_1m_2}\right|$$

証明

　2直線 $y=m_1x+n_1$，$y=m_2x+n_2$ と $x$ 軸の正の向きとのなす角をそれぞれ $\theta_1$，$\theta_2$ (ただし，$0\leqq\theta< \pi,\theta\neq\dfrac\pi2)$ とすると， $$\tan\theta_1=m_1,\ \tan\theta_2=m_2$$ である．
　ここで，$\theta_1-\theta_2=A$ とおくと，2直線のなす鋭角 $\theta$，及び $\tan\theta$ は，$A$ の値によって次の4通りに場合分けされる：

　$[1]\ 0\leqq A\!<\!\dfrac\pi2$ のとき，$\theta\!=\!A$ $$\therefore \tan\theta\!=\!\tan A$$ 　$[2]\ \dfrac\pi2\!<\! A\!<\!\pi$ のとき，$\theta\!=\!\pi\!-\!A$ $$\therefore \tan\theta\!=\!\tan(\pi\!-\!A)\!=\!-\tan A$$ 　$[3]\ -\dfrac\pi2\!<\! A\!<\!0$ のとき，$\theta\!=\!-A$ $$\therefore \tan\theta\!=\!\tan(-A)\!=\!-\tan A$$ 　$[4]\ -\pi\!<\! A\!<\!-\dfrac\pi2$ のとき，$\theta\!=\!\pi\!+\!A$ $$\therefore \tan\theta\!=\!\tan(\pi\!+\!A)\!=\!\tan A$$

　上のいずれの場合も， $$\tan\theta=|\tan A|$$ であるから， $$\begin{align*} \tan\theta&=|\tan A|\\[5pt] &=|\tan(\theta_1-\theta_2)|\\[5pt] &=\left|\frac{\tan\theta_1-\tan\theta_2}{1+\tan\theta_1\tan\theta_2}\right|\\[5pt] &=\left|\frac{m_1-m_2}{1+m_1m_2}\right| \end{align*}$$

■

---

高校数学[総目次]

数学Ⅱ　第4章　三角関数

	スライド	ノート	問題
1. 一般角と弧度法	[会員]
2. 一般角の三角関数	[会員]
3. 三角関数の性質	[会員]		[会員]
4. 三角関数のグラフ	[会員]
5. 三角関数の加法定理	[会員]		[会員]
6. 三角関数の種々の公式	[会員]
7. 三角関数の合成	[会員]
8. 三角関数の応用	[会員]