高校数学[総目次]
数学Ⅲ 第1章 極限
| スライド | ノート | 問題 | |
| 1. 数列の極限 | [無料] | ||
| 2. 無限等比数列 | [無料] | ||
| 3. 無限級数 | |||
| 4. 無限等比級数 | |||
| 5. 関数の極限 | |||
| 6. (sin x)/x の極限 | |||
| 7. 関数の連続性 |

7.0 はじめに
解を具体的にこうだとは言えないが,確かに存在はしている
数学Ⅱの微分のところで次のような問題があった.
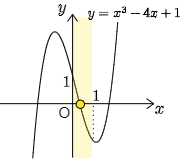
Q. 3次方程式 $x^3-4x+1=0$ が0と1の間に実数解をもつことを示せ.
一般に3次以上の方程式を高次方程式というが,高次方程式の基本解法は,まず発見的に解 $\alpha$ を1つ見つけて,左辺を $x-\alpha$ で割り,因数分解していくというものであった.この方程式の場合,$\alpha$ の候補は $\pm1$ である.ところが $x=1$ も $x=-1$ も解ではないからこの方程式は有理数解をもたない.(この点について詳しくはこちら を参照.) つまり,この方程式を解いて,解を具体的に求めることは簡単にはできないのである.しかしながら,単に実数解の存在を示すだけならば難しくない.方程式の左辺を $f(x)$ とおくと,
\[f(0)=1(>0),\ f(1)=-2(<0)\]
となって $f(0)$ と $f(1)$ は異符号であるから,グラフを考えると必ず0と1の間で $x$ 軸をまたがなければならない.すなわち $x$ 軸との共有点が存在するのである.このことは方程式の実数解の存在を示したことに他ならない.
$f(a)$ と $f(b)$ が異符号だけでは解の存在は保証されない
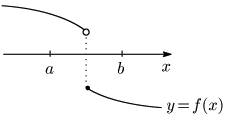
ところが別の方程式 $f(x)=0$ について, $f(x)$ のグラフが次のようであると,
$f(a)$ と $f(b)$ が異符号$\iff f(x)=0$ は $a$ と $b$ の間に実数解をもつ $\cdots$(☆)
とはいえない.グラフがつながっておらず,$x$ 軸と共有点をもっていないからである.つまり(☆)は無条件では成り立たない.グラフがつながっているという条件(仮定)が必要なのだ.それではグラフがつながっているというのを数学的に定式化するとどうなるのか.それが関数の連続性というものである.
7.1 関数が連続であるための条件
連続かどうかは各値によって決められる
関数の連続性は定義域に属する各値に対して連続かどうかが決められるものである.例えば,ある関数 $f(x)$ は,$x=1$ では連続だけど $x=2$ では連続ではない等々.では連続かどうかを判定するにはどうしたらよいか.それは次に示す3つのステップをすべてクリアしたとき,連続であるというのである:
$x=a$ で連続であるとは 関数 $f(x)$ が $x=a$ で連続であるということは,次の3つが満たされているときをいう:
- $x=a$ は $f(x)$ の定義域に属する.
( $f(a)$ が定義されている.) - 極限値 $\displaystyle\lim_{x\to a}f(x)$ が存在する.
- $\displaystyle\lim_{x\to a}f(x)=f(a)$ である.
①を満たし,②,③のいずれか一方でも満たさない場合に,$f(x)$
は $x=a$ で不連続であるという.
従って例えば「関数 $\dfrac 1x$ は,$x=0$ で不連続である」とは言わない.($\dfrac 1x$ は $x=0$ で定義されていないから①を満たさない.)
例1
$f(x)=\left\{
\begin{array}{ll}
0&(x=0\ \mbox{のとき})\\
x^2+1&(x\neq 0\ \mbox{のとき})
\end{array}\right.$ について,$x=0$ での連続性を調べよ.

