バウムクーヘン分割-基本的な考え方と証明・教科書的解法との比較

　このページにある内容は，例とともにこちらのスライドでわかり易く説明しています．

※PC環境なら全画面表示でより見やすく，よりわかりやすい！

高校数学ワンポイント

	スライド	ノート
1. ファクシミリの原理
2. バウムクーヘン分割
3. 円と放物線
4. 垂線の長さ
5. 不定方程式
6. 関数の連続性は導関数に遺伝するか
7. 極方程式における $𝑟$ の正負について
8. 極座標表示における扇形分割積分
9. 素因数分解の一意性
10. 三角関数の不定積分
11. コーシー・シュワルツの不等式
12. 放物線と2接線で囲まれた部分の面積
13. 整式の除法(発展編)
14. 3次関数のグラフの特徴
15. 曲線の長さを求める公式の証明について
16. もう迷わない！必要条件・十分条件のくすっと笑える判定方法
17. 同じものを含む円順列の考え方
18. $𝑓 (𝑓 (𝑥)) = 𝑥$ の形をした関数方程式の取り扱い方
19. パラメータが2次で表された直線の通過領域
20. 四面体の面上及び内部を表すベクトル

バウムクーヘン分割

　 $𝑥$ 軸まわりの回転体の体積は， $𝑥$ 軸に垂直な平面での切り口の面積が大抵の場合簡単に表示できますが， $𝑦$ 軸まわりの回転体の体積を計算しようと思うと， $𝑦$ 軸に垂直な平面での切り口の面積が簡単には表せない場合があり， $𝑥$ 軸まわりの回転体の計算に比べてぐっと難易度が上がります．その抜け道的な存在がバウムクーヘン分割と呼ばれる積分方法です．この用語は「大学への数学」でおなじみの東京出版の書物で用いられていましたが，今や大手の参考書などにも用語として掲載されるほど一般的な考え方になってきました．

　以下のノートではバウムクーヘン分割の概要とその証明，イメージ図を掲載していますが，スライド では例題を用いて教科書的な解法と，バウムクーヘン分割を用いた解法の両方を説明しています．そしてスライドの最後には，教科書的な説明からバウムクーヘン分割にもっていく考え方も説明していますので是非ご覧ください．

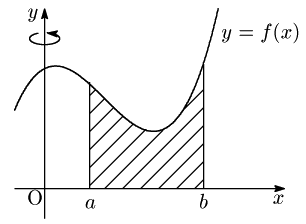
バウムクーヘン分割

　図の斜線部分を $𝑦$ 軸のまわりに1回転させてできる立体の体積は，

$\int 𝑏 𝑎 2 𝜋 𝑥 𝑓 (𝑥) 𝑑 𝑥$

証明

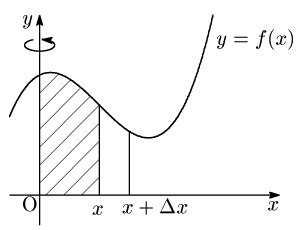
　図の斜線部分を $𝑦$ 軸のまわりに1回転させてできる立体の体積を $𝑉 (𝑥)$ とします．すると求める体積は

$𝑉 (𝑏) - 𝑉 (𝑎)$

です．

　 $𝑥$ が微小量 $Δ 𝑥 (> 0)$ だけ変化したときの体積の変化量 $𝑉 (𝑥 + Δ 𝑥) - 𝑉 (𝑥)$ は， $𝑥$ から $𝑥 + Δ 𝑥$ までの $𝑓 (𝑥)$ の最大値，最小値をそれぞれ $𝑀, 𝑚$ とすれば $𝜋 (𝑥 + Δ 𝑥) 2 𝑚 - 𝜋 𝑥 2 𝑚 ≦ 𝑉 (𝑥 + Δ 𝑥) - 𝑉 (𝑥) ≦ 𝜋 (𝑥 + Δ 𝑥) 2 𝑀 - 𝜋 𝑥 2 𝑀$ と評価できます．左辺と右辺を計算して， $2 𝜋 𝑥 𝑚 Δ 𝑥 + 𝜋 𝑚 (Δ 𝑥) 2 ≦ 𝑉 (𝑥 + Δ 𝑥) - 𝑉 (𝑥) ≦ 2 𝜋 𝑥 𝑀 Δ 𝑥 + 𝜋 𝑀 (Δ 𝑥) 2 .$ 　各辺を正の数 $Δ 𝑥$ で割って， $2 𝜋 𝑥 𝑚 + 𝜋 𝑚 Δ 𝑥 ≦ 𝑉 (𝑥 + Δ 𝑥) - 𝑉 (𝑥) Δ 𝑥 ≦ 2 𝜋 𝑥 𝑀 + 𝜋 𝑀 Δ 𝑥 .$ 　ここで， $Δ 𝑥 \to + 0$ のとき， $𝑀 \to 𝑓 (𝑥), 𝑚 \to 𝑓 (𝑥)$ となりますから，はさみうちの原理より中辺は， $l i m Δ 𝑥 \to + 0 𝑉 (𝑥 + Δ 𝑥) - 𝑉 (𝑥) Δ 𝑥 = 2 𝜋 𝑥 𝑓 (𝑥)$ です． $Δ 𝑥 < 0$ のときも同様にして $Δ 𝑥 \to - 0$ の極限を考えると， $l i m Δ 𝑥 \to - 0 𝑉 (𝑥 + Δ 𝑥) - 𝑉 (𝑥) Δ 𝑥 = 2 𝜋 𝑥 𝑓 (𝑥)$ となりますから，結局 $l i m Δ 𝑥 \to 0 𝑉 (𝑥 + Δ 𝑥) - 𝑉 (𝑥) Δ 𝑥 = 2 𝜋 𝑥 𝑓 (𝑥)$ となります．ところで，左辺の $l i m Δ 𝑥 \to 0 𝑉 (𝑥 + Δ 𝑥) - 𝑉 (𝑥) Δ 𝑥$ は， $𝑉' (𝑥)$ の定義式に他なりませんから， $𝑉' (𝑥) = 2 𝜋 𝑥 𝑓 (𝑥)$ です．つまり， $𝑉 (𝑥)$ の導関数が $2 𝜋 𝑥 𝑓 (𝑥)$ なのですから $𝑉 (𝑥)$ は $2 𝜋 𝑥 𝑓 (𝑥)$ の不定積分の1つであるということがわかりました．よって求める体積は， $𝑉 (𝑏) - 𝑉 (𝑎) = [𝑉 (𝑥)] 𝑏 𝑎 = \int 𝑏 𝑎 𝑉' (𝑥) 𝑑 𝑥 = \int 𝑏 𝑎 2 𝜋 𝑥 𝑓 (𝑥) 𝑑 𝑥$ となるのです．

■

補足

　円筒形を，縦に切り込みを入れて展開すると， $Δ 𝑥$ が十分小さいとき，概略直方体になります：

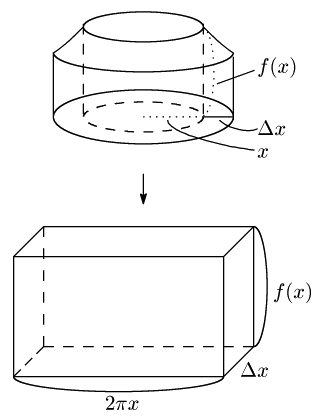
　この直方体の体積は $2 𝜋 𝑥 𝑓 (𝑥) Δ 𝑥$ です．円筒形の体積を直方体の体積で近似して，足し上げていったものがバウムクーヘン分割の式といえます．

高校数学[総目次]

高校数学ワンポイント

	スライド	ノート
1. ファクシミリの原理
2. バウムクーヘン分割
3. 円と放物線
4. 垂線の長さ
5. 不定方程式
6. 関数の連続性は導関数に遺伝するか
7. 極方程式における $𝑟$ の正負について
8. 極座標表示における扇形分割積分
9. 素因数分解の一意性
10. 三角関数の不定積分
11. コーシー・シュワルツの不等式
12. 放物線と2接線で囲まれた部分の面積
13. 整式の除法(発展編)
14. 3次関数のグラフの特徴
15. 曲線の長さを求める公式の証明について
16. もう迷わない！必要条件・十分条件のくすっと笑える判定方法
17. 同じものを含む円順列の考え方
18. $𝑓 (𝑓 (𝑥)) = 𝑥$ の形をした関数方程式の取り扱い方
19. パラメータが2次で表された直線の通過領域
20. 四面体の面上及び内部を表すベクトル

このページで疑問は解決されましたか？

　こちら から数学に関するご質問・ご要望をお寄せください。