3．円と放物線(ノート)

高校数学[総目次]

高校数学ワンポイント

	スライド	ノート
1. ファクシミリの原理	[会員]
2. バウムクーヘン分割	[会員]
3. 円と放物線
4. 垂線の長さ
5. 不定方程式
6. 関数の連続性は導関数に遺伝するか
7. 極方程式における $r$ の正負について
8. 極座標表示における扇形分割積分
9. 素因数分解の一意性
10. 三角関数の不定積分
11. コーシー・シュワルツの不等式
12. 放物線と2接線で囲まれた部分の面積
13. 整式の除法(発展編)
14. 3次関数のグラフの特徴
15. 曲線の長さを求める公式の証明について
16. もう迷わない！必要条件・十分条件のくすっと笑える判定方法
17. 同じものを含む円順列の考え方
18. $f(f(x))=x$ の形をした関数方程式の取り扱い方
19. パラメータが2次で表された直線の通過領域
20. 四面体の面上及び内部を表すベクトル

１．異なる4点で交わる場合

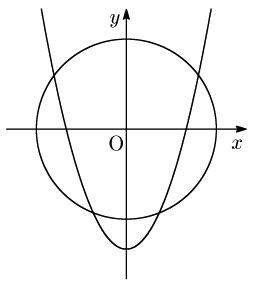
簡単のために，円と放物線の方程式をそれぞれ $$\left\{ \begin{array}{lr} x^2+y^2=1,&\ \ \ \cdots ①\\ y=x^2+k&\ \ \ \cdots ② \end{array} \right.$$ としておきます．放物線は軸が直線 $x=0$ ですから $y$ 軸に関して対称です．そして次の問題を考えてみましょう．

A.　円と放物線が異なる4点で交わる必要かつ十分なる条件は

①かつ②を満たす異なる4つの実数の組 $\boldsymbol{(x,\ y)}$ が存在すること　　$\cdots$ (＊)

です．方針は概ね次の2つです：

1. $y$ を消去して $x$ の4次方程式を作る．
2. $x$ を消去して $y$ の2次方程式を作る．

まず方針1

　②を①に代入して $y$ を消去すると $$\begin{gather*} x^2+(x^2+k)^2=1.\\[5pt] \therefore\ \ x^4+(2k+1)x^2+k^2-1=0. \end{gather*}$$ 　従ってこの $\boldsymbol{x}$ の4次方程式が異なる4つの実数解をもてば，上の(＊)が満たされます．何故なら，

②式により $\boldsymbol{x}$ に応じて実数 $\boldsymbol{y}$ がただ1つ決まるから

です．$x^2=t$ とおくと $t\geqq 0$ ですから $$t^2+(2k+1)t+k^2-1=0$$ が異なる2つの正の解(下の[注]参照)をもつ条件を求めればよいことがわかります． $$\begin{gather*} -\frac{2k+1}2>0,\ (2k+1)^2-4(k^2-1)>0,\ k^2-1 > 0.\\[5pt] \therefore k<-\frac 12,\ \mbox{かつ}\ \ k>-\frac 54,\ \mbox{かつ}\ k<-1,\ 1< k.\\[5pt] \therefore -\frac 54< k<-1.\ \ \cdots (\mbox{答}) \end{gather*}$$

　異なる2つの正の解をもつための条件である3本の不等式は左から順に，軸，判別式，$\boldsymbol{t\!=\!0}$ での値 についての各条件です．（詳しくは2次方程式の解の配置 参照．）

次に方針2

　②より $$x^2=y-k.\ \ \ \cdots ③$$ 　これを①に代入して $$\begin{gather*} (y-k)+y^2=1.\\[5pt] \therefore\ y^2+y-k-1=0. \end{gather*}$$

　ここで(＊)の条件が，この $\boldsymbol{y}$ の2次方程式が異なる2つの実数解を持つことではないことに注意します．何故なら

③式より $\boldsymbol{y}$ に応じた実数 $\boldsymbol{x}$ が存在するとは限らない

からです．③より $x^2=y-k\geqq 0$ ですから，(＊)の条件は「$y$ の2次方程式が $y>k$ (下の[注]参照)に異なる2つの実数解を持つこと」です．よって $$\begin{gather*} -\frac 12>k,\ 1^2-4(-k-1)>0,\ k^2+k-k-1>0.\\[5pt] \therefore\ \ k<-\frac 12,\ \mbox{かつ}\ k>-\frac 54,\ \mbox{かつ}\ k<-1,\ 1< k.\\[5pt] \therefore\ \ -\frac 54 < k<-1.\ \ \cdots (\mbox{答}) \end{gather*}$$

　$y>k$ に異なる2つの実数解をもつための条件である3本の不等式は左から順に，軸，判別式，$\boldsymbol{t\!=\!k}$ での値 についての各条件です．（詳しくは2次方程式の解の配置 参照．）

補足

　③より「$y-k>0$ の範囲に実数解を持つ」としましたが，$y-k=1-y^2>0$ ですから「$-1<y<1$ の範囲に実数解を持つ」としてもよいでしょう．

2．接する場合

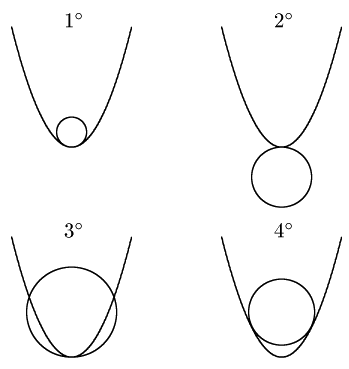
　放物線の軸上に中心がある円が，その放物線と接するとき，位置関係について，図の4タイプが考えられます．入試では$1^\circ$と$4^\circ$が頻出です．$1^\circ$～$3^\circ$は接点が放物線の頂点の場合です．

2.1　タイプ1$^\circ$

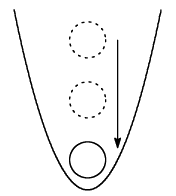
　放物面のグラスに球を落とすとき，果たして球はグラスの底に達するでしょうか？タイプ$4^\circ$を見れば，球の半径がある値を超えてしまうとそれは叶わないことがわかります．となれば，底に到達する球の半径の最大値に興味があるでしょう．

Q.　放物線 $y=x^2\ \ \cdots ①$について，タイプ$1^\circ$になる円の半径の最大値を求めなさい．

A.　タイプ$1^\circ$になるとき，円の方程式は $$x^2+(y-b)^2=b^2 \ \ \cdots \mbox{②}$$ とおけます．
　まず①，②の2つの図形は共有点$\boldsymbol{(0,\ 0)}$をもつことに注意をしておきます．$x$ を消去すると $$\begin{gather*} y+(y-b)^2=b^2,\\[5pt] y^2-(2b-1)y=0,\\[5pt] y\{y-(2b-1)\}=0,\\[5pt] \therefore\ \ y=0,\ 2b-1 \end{gather*}$$ 　タイプ$1^\circ$ では①と②を満たす実数の組 $(x,\ y)$ を $(0,\ 0)$ の1組しかもちません．$y>0$ の解を持つと，①よりその $y$ に応じて実数 $x$ が $\pm \sqrt y$ と2つ現れます．これはタイプ$3^\circ$ です．従って $$2b-1\leqq 0\ \ \therefore b\leqq \frac 12.$$ 　よって半径の最大値は $\dfrac 12$ です．

2.2　 タイプ2$^\circ$

　円と放物線の方程式をそれぞれ
$$\left\{\begin{array}{l} x^2+(y-b)^2=b^2,\\ y=x^2 \end{array} \right.$$ とすれば，$b<0$ のケースです．

2.3　 タイプ3$^\circ$

　$1^\circ$で議論済みです．

2.4　 タイプ4$^\circ$

Q.　円と放物線の方程式をそれぞれ $$\left\{ \begin{array}{lr} x^2+(y-b)^2=1,&\ \ \ \cdots \mbox{①}\\ y=x^2&\ \ \ \cdots \mbox{②} \end{array} \right.$$ とする．タイプ$4^\circ$ のようになるとき，$b$ の値を求めなさい．

A.　$x$ を消去すると $$\begin{gather*} y+(y-b)^2=1,\\[5pt] \therefore\ \ y^2-(2b-1)y+b^2-1=0. \end{gather*}$$ 　この $y$ の2次方程式が正の重解を持てばよいのですから $$\begin{gather*} \frac{2b-1}2>0,\ (2b-1)^2-4(b^2-1)=0.\\[5pt] \therefore\ b=\frac 54.\ \ \cdots (\mbox{答}) \end{gather*}$$

補足

　放物線上の点 $(t,\ t^2)$ と円の中心 $(0,\ b)$ との距離の平方は $$t^2+(t^2-b)^2=t^4-(2b-1)t^2+b^2$$ となり，$t^2$ の2次関数が $t^2>0$ において最小値1をとるための条件を求めればよいことがわかります．それは $$\frac{2b-1}2>0,\ かつ\ -\frac{(2b-1)^2}4+b^2=1$$ であり，第2式は結局解答の $(\mbox{判別式})=0$ と同じになります． 詳しくは次項の「●別の考え方」をご覧ください．

● 別の考え方

　タイプ $1^\circ$ とタイプ $4^\circ$ は，円の中心から放物線までの距離の最小値に着目した次のような考え方もできます．視覚的に理解しやすく，オススメの考え方です

設定　中心 ${\rm C}(0,b)$ (ただし $b>0)$の円が，放物線 $y=x^2$ と接する．

　放物線上の点を ${\rm P}(t,t^2)$ とおくと，円の中心 ${\rm C}(0,b)$ との距離の2乗は，

$$\begin{align*} {\rm CP}^2&=(t-0)^2+(t^2-b)^2\\[5pt] &=t^4-(2b-1)t^2+b^2\\[5pt] &=\left(t^2-\frac{2b-1}2\right)^2+b-\frac14 \end{align*}$$

です．ここで $t^2=X(\geqq0)$ とおくと，

$${\rm CP}^2=\left(X-\frac{2b-1}2\right)^2+b-\frac14\hspace{5mm}(X\geqq0)$$

となります．円と放物線が接するとき，$\rm CP$ の最小値が円の半径と等しくなっていることに注意しておきましょう．

$1^\circ$　球が放物面のグラスの底に達するケース

　$\rm CP^2$ の最小値が $t=0$ すなわち $X=0$ で実現されるケースです．定義域が $X\geqq 0$ ですからグラフの軸を考えると，$\dfrac{2b-1}2\leqq0$ すなわち $(0<)\,b\leqq\dfrac12$ となっていなければなりません．このような $b$ の値の範囲のとき，円と放物線の位置関係はタイプ$1^\circ$ となるのです．そしてこの場合，$b$ の値が半径そのものになっていますから，グラスの底に達する球の半径は最大で $\dfrac12$ です．

$4^\circ$　接点の $x$ 座標 $t$ が原点以外のケース

　$\rm CP^2$ の最小値が $t>0$ すなわち $X>0$ で実現されるケースですから，$\dfrac{2b-1}2>0$ すなわち $b>\dfrac12$ となっていなければなりません．この場合 $\rm CP^2$ は $X=\dfrac{2b-1}2$ のとき最小値　$b-\dfrac14$ をとり，これが与えられた円の半径の2乗に等しくなるわけですから，

$$b-\frac14=1^2\ \ \ \ \therefore b=\frac54$$

となり，上で見た同じ結果が得られました．

3．その他のケース

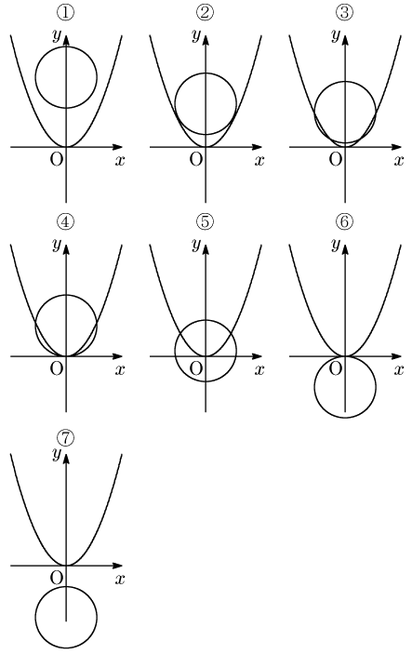
　先のタイプ$4^\circ$でみた $$\left\{ \begin{array}{l} x^2+(y-b)^2=1,\\ y=x^2 \end{array} \right.$$ について，円の中心の $y$ 座標である $b$ の値で分類すると上の①～⑦が考えられます．ここで $x$ を消去して得られる $y$ の2次方程式 $$y^2-(2b-1)y+b^2-1=0$$ は一体どんな解を持つでしょうか．準備として判別式 $D$ を計算しておくと $$D=(2b-1)^2-4(b^2-1)=-4b+5$$ となります．

1. ① $b > 5/4$ のケースですから $D < 0$，即ち異なる2つの虚数解を持つ場合です．
2. ② $b=5/4$ のケースですから $D=0$，即ち重解を持つ場合です．
3. ③ $1 < b < 5/4$ のケースですから $D > 0$ であり，異なる2つの正の実数解を持つ場合です．
4. ④ $b=1$ のケースですから $D > 0$ であり，0と正の実数解を持つ場合です．
5. ⑤ $-1 < b < 1$ のケースですから $D > 0$ であり，正負の2つの実数解を持つ場合です．
6. ⑥ $b=-1$ のケースですから $D > 0$ であり，0と負の実数解を持つ場合です．
7. ⑦ $b < -1$ のケースですから $D > 0$ であり，異なる2つの負の実数解を持つ場合です．

　②，④，⑥は円と放物線が接していますが，このうち④，⑥は $D > 0$ です．即ち

円と放物線が接する場合，必ずしも $\boldsymbol{D=0}$ に結びつかない

ことに注意しなければなりません．

---

高校数学[総目次]

	スライド	ノート
1. ファクシミリの原理	[会員]
2. バウムクーヘン分割	[会員]
3. 円と放物線
4. 垂線の長さ
5. 不定方程式
6. 関数の連続性は導関数に遺伝するか
7. 極方程式における $r$ の正負について
8. 極座標表示における扇形分割積分
9. 素因数分解の一意性
10. 三角関数の不定積分
11. コーシー・シュワルツの不等式
12. 放物線と2接線で囲まれた部分の面積
13. 整式の除法(発展編)
14. 3次関数のグラフの特徴
15. 曲線の長さを求める公式の証明について
16. もう迷わない！必要条件・十分条件のくすっと笑える判定方法
17. 同じものを含む円順列の考え方
18. $f(f(x))=x$ の形をした関数方程式の取り扱い方
19. パラメータが2次で表された直線の通過領域
20. 四面体の面上及び内部を表すベクトル