受験数学において，「ファクシミリの原理」と呼ばれる魅力的な考え方があります．「大学への数学(東京出版)」で用いられている大変印象的な用語で，考え方の本質を「ファクシミリ」になぞらえているところがユニークでもあります．
ファクシミリの原理という考え方の基本は，簡単な例題を用いてスライド で解説していますのでそちらをご覧ください．ここでは京都大学と東京大学の本格的な問題を用いて，自然な発想でのやり方と，ファクシミリの原理を用いたやり方の2通りで説明してみます．
高校数学[総目次]
高校数学ワンポイント
| スライド | ノート | |
| 1. ファクシミリの原理 | [会員] | |
| 2. バウムクーヘン分割 | [会員] | |
| 3. 円と放物線 | ||
| 4. 垂線の長さ | ||
| 5. 不定方程式 | ||
| 6. 関数の連続性は導関数に遺伝するか | ||
| 7. 極方程式における $r$ の正負について | ||
| 8. 極座標表示における扇形分割積分 | ||
| 9. 素因数分解の一意性 | ||
| 10. 三角関数の不定積分 | ||
| 11. コーシー・シュワルツの不等式 | ||
| 12. 放物線と2接線で囲まれた部分の面積 | ||
| 13. 整式の除法(発展編) | ||
| 14. 3次関数のグラフの特徴 | ||
| 15. 曲線の長さを求める公式の証明について | ||
| 16. もう迷わない！必要条件・十分条件のくすっと笑える判定方法 | ||
| 17. 同じものを含む円順列の考え方 | ||
| 18. $f(f(x))=x$ の形をした関数方程式の取り扱い方 | ||
| 19. パラメータが2次で表された直線の通過領域 | ||
| 20. 四面体の面上及び内部を表すベクトル |
1．京都大学の過去問
答その1 [自然な発想]
$L:y=2x\ (0\leqq x\leqq1)$ と表されますから，曲線 $y=x^2+ax+b$ が $L$ と共有点をもつための条件は，2次方程式 $x^2+ax+b=2x$ 即ち
\[x^2+(a-2)x+b=0\]
が，$0\leqq x\leqq1$ の範囲に少なくとも1つの解をもつことです．
$f(x)=x^2+(a-2)x+b$ とおくと，放物線 $y=f(x)$ は下に凸で，軸は直線 $x=-\dfrac{a-2}2$ です．
方程式 $f(x)=0$ が $0\leqq x\leqq1$ の範囲に少なくとも1つの解をもつのは，次の[1], [2] の場合が考えられます：
[1] $f(0)=0$ または $f(1)=0$ のとき，即ち $b=0$ または $a+b-1=0$ のとき
このときは題意を満たします．
[2] $f(0)\neq0$ かつ $f(1)\neq0$ のとき，即ち $b\neq0$ かつ $a+b-1\neq0$ のとき
$1^\circ$ 重解を含む2解がともに $0 < x < 1$ の範囲にあるとき
このとき，$f(x)=0$ の判別式を $D$ とすると，
\[\begin{align*}
&\left\{\begin{array}{l}
\\
D=(a-2)^2-4b\geqq0\\[5pt]
\mbox{軸}:0 < -\dfrac{a-2}2 < 1\\[5pt]
f(0)=b > 0\\[5pt]
f(1)=a+b-1 > 0
\end{array}\right.\\
\therefore\ \ &\left\{\begin{array}{l}
\\
b\leqq \dfrac{(a-2)^2}4\\[5pt]
0 < a < 2\\[5pt]
b > 0\\[5pt]
b > -a+1
\end{array}\right.
\end{align*}\]
$2^\circ$ $0 < x < 1$ にただ1つの解をもつとき
\[f(0)f(1) < 0\ \mbox{即ち}\ b(a+b-1) < 0\]
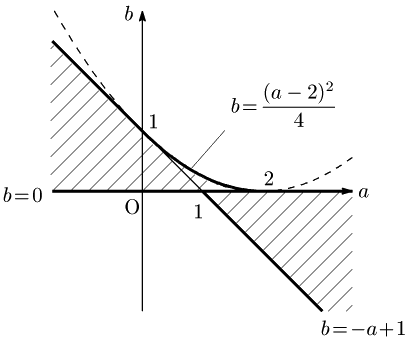
以上により，実数の組 $(a,b)$ の集合は，図の斜線部分のようになります．ただし境界線を含みます．
補足1
2次方程式の解の配置については，数学Ⅰ 第1章 2次関数 7. 2次方程式の解の配置のスライド，及び【ノート】をご覧ください．
補足2
上の方法では2次方程式 $x^2+(a-2)x+b=0$ が，$0\leqq x\leqq1$ の範囲に少なくとも1つの解をもつことを直接に求めましたが，否定の範囲を計算してその補集合を考えるのでもよいでしょう．この場合否定は「2次方程式 $x^2+(a-2)x+b=0$ が，$0\leqq x\leqq1$ の範囲に解を持たない」となりますから，その条件は $f(x)=x^2+(a-2)x+b$ とおくと
$\mbox{min}\left\{f(0),\ f(1),\ f\left(-\dfrac{a-2}2\right)\right\}>0$ または
$\mbox{max}\left\{f(0),\ f(1)\right\}<0$
即ち
「$b\!>\!0$ かつ $a\!+\!b\!-\!1\!>\!0$ かつ $b\!-\!\dfrac{(a-2)^2}4\!>\!0$」または
「$b<0$ かつ $a+b-1<0$」
です．ただし $f\!\left(\!-\dfrac{a\!-\!2}2\right)$ は，放物線の軸が定義域内に入っている $0\leqq-\dfrac{a-2}2\leqq1$ 即ち $0\leqq a\leqq 2$ の範囲のみで有効になります．この範囲を図示すれば，上図の斜線が施されていない部分となります．ただし境界線は含みません．
※ max，min の部分の詳しい考え方については，数学Ⅰ 第1章 2次関数 3. 2次関数の最大・最小のスライド ，及び ノート をご覧ください．
答その2 [ファクシミリの原理]
$x^2+(a-2)x+b=0\ \cdots$ ① が $0\leqq x\leqq 1$ の範囲に少なくとも1つの解をもつ $(a,\ b)$ の条件を求めればよいわけですが，そのために①を変形して
$b=-x^2-(a-2)x\ \cdots$ ②
としておきます．そして次がファクシミリの原理という考え方のポイントです．
$\boldsymbol{a}$ を固定する
すると，②の右辺は $x$ の2次関数であり．これを $f(x)$ とおくとき，
$\boldsymbol{b=f(x)}$ の値域を調べる
ということを行います．このように固定した値に対して値域を探るという手法を「ファクシミリの原理」と呼んでいるわけです．
これをイメージとして捉えると次のようになります．座標平面というキャンバスに幾何学的な模様が描かれているとします．しかしシートで全体が覆われており，その模様が見えません．シートには小さなスリットが1つあり，この隙間部分だけは見えていますが，細すぎて全体像がつかめません．幸い，このシートは $x$ 軸方向に移動可能だったので，右側にずらしていくと，隠れていた模様が少しずつ見えて全体像をつかむことができます．
さて，固定した $a$ に対して関数 $b=f(x)$ の値域を調べる訳ですから，2次関数の最大・最小問題に帰着されます．もし $f(x)$ が3次以上の関数ならば微分によって値域を探ります＊．
[＊] 例えば東京大学(1997)で次の問題が出題されましたが，考察の対象が3次関数となるので微分によって値域を求めます．この問題の解説は，高校数学ワンポイント パラメータが2次で表された直線の通過領域 のページを参照してください．
[東京大学1997]
$0\leqq t\leqq1$ を満たす実数 $t$ に対して， $xy$ 平面上の点 $\rm{A,\ B}$を ${\rm A}\left(\dfrac{2(t^2+t+1)}{3(t+1)},\ -2\right)$，${\rm B}\left(\dfrac23t,\ -2t\right)$ と定める．$t$ が $0\leqq t\leqq 1$ を動くとき，直線ABの通りうる範囲を図示せよ．
\[f(x)=-\left(x+\frac{a-2}2\right)^2+\frac{(a-2)^2}4\]
となり，グラフは上に凸ですから，$0\leqq x\leqq 1$ における $f(x)$ の値域は
\[ {\rm min}\{f(0),f(1)\}\leqq f(x)\leqq{\rm max}\left\{\!f(0),f(1),f\!\left(\!-\frac{a\!-\!2}2\!\right)\!\right\} \]
つまり，
\[ {\rm min}\{0,-a+1\}\leqq b\leqq{\rm max}\left\{\!0,-a+1,\frac{(a-2)^2}4\!\right\} \]
となります．ただし，右辺の $f\!\left(\!-\dfrac{a\!-\!2}2\right)$ は，軸が定義域内に入っている $0\leqq-\dfrac{a-2}2\leqq1$ 即ち $0\leqq a\leqq 2$ の範囲のみで有効になります．
以上により，実数の組 $(a,\ b)$ の集合は上の図の境界を含む斜線部分となります．
※ max，min の部分の詳しい考え方については，数学Ⅰ 第1章 2次関数 3. 2次関数の最大・最小のスライド ，及び ノート をご覧ください．
研究～包絡線から捉える～
$x$ を固定すると，$ab$ 平面上において，$x^2+(a-2)x+b=0\ (\cdots$☆) 即ち $b=-xa-x^2+2x$ は直線を表します．☆を $x$ について平方完成すると $\left(x+\dfrac{a-2}2\right)^2+b-\dfrac{(a-2)^2}4=0$ となりますから，この直線は放物線 $b=\dfrac{(a-2)^2}4$ の $a=2-2x\ (0\leqq x\leqq1)$ における接線の方程式です．従って，上の図の斜線領域は，接点の $a$ 座標が $0\leqq a \leqq 2$ と変化するときの接線の通過領域となっています．詳しくは，高校数学ワンポイント19．パラメータが2次で表された直線の通過領域 を参照してください．
2．東京大学の過去問
問題2 座標平面上の2点P，Qが，曲線 $y=x^2$ $(-1\leqq x\leqq 1)$ 上を自由に動くとき，線分PQを $1:2$ に内分する点Rが動く範囲を $D$ とする．ただし，P=Q のときは R=P とする．
(1) $a$ を $-1\leqq a\leqq1$ を満たす実数とするとき，点 $(a,b)$ が $D$ に属するための $b$ の条件を $a$ を用いて表せ．
(2) $D$ を図示せよ．
(東京大)
答その1 [自然な発想]
対称性より $0\leqq a\leqq1$ とします．
P$(p,p^2)$，Q$(q,q^2)$ $(-1\leqq p\leqq1,\ -1\leqq q\leqq1)$ とおくと，$a,b$ は
$\left\{ \begin{array}{l} a=\dfrac{2p+q}{1+2}\\[5pt] b=\dfrac{2p^2+q^2}{1+2} \end{array}\right.$
すなわち
$ \left\{\begin{array}{ll} q=3a-2p&\cdots\ \mbox{①}\\[5pt] 2p^2+q^2-3b=0&\cdots\ \mbox{②} \end{array}\right.$
を満たします．①と②から $q$ を消去して整理すると
$2p^2-4ap+3a^2-b=0\ \cdots$ ③
を得ます．従って題意は
$p$ の方程式③が $-1\leqq p\leqq1$ かつ $-1\leqq q\leqq1$ をともに満たす範囲に少なくとも1つ解をもつ $a,b$ の条件を求めること
と同値です．$-1\leqq q\leqq1$ の部分は①より $-1\leqq 3a-2p\leqq 1$，すなわち
$\dfrac32a-\dfrac12\leqq p\leqq\dfrac32a+\dfrac12\ \cdots$ ④
と $p$ の条件に置き換えることができます．また③の左辺を $p$ の2次関数とみて $f(p)$ とおきますと
\[f(p)=2(p-a)^2+a^2-b\]
となり，このグラフの軸は直線 $p=a$ ですが，$p=a$ は常に④の範囲内の値であることに注意します．実際，$0\leqq a\leqq1$ により
\[\begin{align*} &a-\left(\frac32a-\frac12\right)=\frac{1-a}2\geqq0\\[5pt] &\left(\frac32a+\frac12\right)-a=\frac{a+1}2\geqq0 \end{align*}\]
となっていることから理解できます．
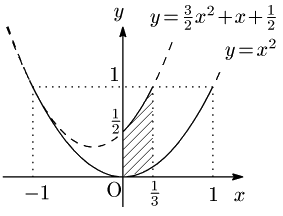
1° $\boldsymbol{0\leqq a\leqq\dfrac13}$ のとき
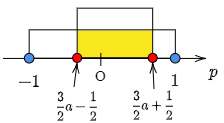
$-1\leqq p\leqq1$ かつ ④の共通範囲は $\dfrac32a-\dfrac12\leqq p\leqq\dfrac32a+\dfrac12$ です．放物線 $y=f(p)$ の軸 $p=a$ がこの範囲にあることに注意すると，両端の値のうち，より軸から遠いのは $p=\dfrac32a+\dfrac12$ の方です．よってこの範囲に方程式③が少なくとも1つ解をもつ条件は，
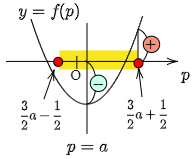
\[f(a)\leqq0,\ f\left(\frac32a+\frac12\right)\geqq0\]
\[\therefore a^2-b\leqq0,\ \frac32a^2+a+\frac12-b\geqq0\]
\[\therefore a^2\leqq b\leqq \frac32a^2+a+\frac12\]
よってこのとき点 $(a,b)$ の存在範囲は次のようになります．
2° $\boldsymbol{\dfrac13\leqq a\leqq 1}$ のとき
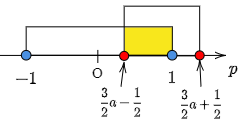
$-1\leqq p\leqq1$ かつ ④の共通範囲は $\dfrac32a-\dfrac12\leqq p\leqq1$ です．この範囲に方程式③が少なくとも1つ解をもつ条件は，
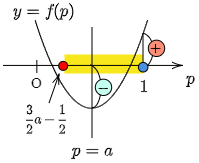
\[f(a)\leqq0,\ f(1)\geqq0\]
\[\therefore a^2-b\leqq0,\ 2-4a+3a^2-b\geqq0\]
\[\therefore a^2\leqq b\leqq 3a^2-4a+2\]
よってこのとき点 $(a,b)$ の存在範囲は次のようになります．
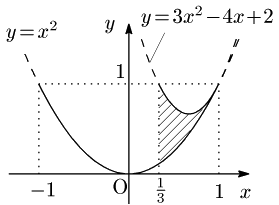
以上の準備の下で，(2)より解答していきます．
(2) $0\leqq a\leqq1$ における $a,b$ の条件が求まりましたから，対称性により領域 $D$ は図の境界線を含む斜線部分になります：
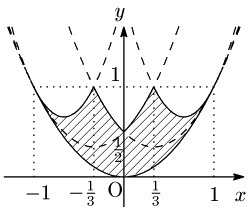
(1) また，この図から $-1\leqq a\leqq1$ における $a,b$ の条件は
\[\begin{align*} -1\leqq a\leqq-\dfrac13\mbox{のとき},\hspace{2mm} &a^2\leqq b\leqq 3a^2+4a+2\\[5pt] -\dfrac13\leqq a\leqq0\mbox{のとき},\hspace{2mm} &a^2\leqq b\leqq \dfrac32a^2-a+\dfrac12\\[5pt] 0\leqq a\leqq\dfrac13\mbox{のとき},\hspace{2mm} &a^2\leqq b\leqq \dfrac32a^2+a+\dfrac12\\[5pt] \dfrac13\leqq a\leqq1\mbox{のとき},\hspace{2mm}& a^2\leqq b\leqq 3a^2-4a+2 \end{align*}\]
となります．
答その2 [ファクシミリの原理]
答その1の①②式までは同じです．③式を
$b=2p^2-4ap+3a^2\ \cdots$ ③’
というように $b$ について解いた表現にしておきます．そして次がファクシミリの原理という考え方のポイントです．
$\boldsymbol a$ を固定する
すると，③’の右辺は $p$ の2次関数であり．これを $f(p)$ とおくとき，
$\boldsymbol {b=f(p)}$ の値域を調べる
ということを行います．$f(p)$ の定義域は，答その1で確認したように$-1\leqq p\leqq1$ かつ $-1\leqq q\leqq1$ から得られる $-1\leqq p\leqq1$ と $\dfrac32a-\dfrac12\leqq p\leqq\dfrac32a+\dfrac12$ の共通範囲です．また，$f(p)$ のグラフの軸である $p=a$ がいかなる場合もこの共通範囲に属している点に注意することも同様です．
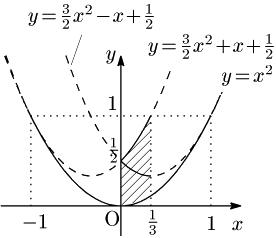
1° $\boldsymbol{0\leqq a\leqq\dfrac13}$ のとき
$f(p)$ の定義域は $\dfrac32a-\dfrac12\leqq p\leqq\dfrac32a+\dfrac12$ となりますから $b=f(p)$ の値域は
\[f(a)\leqq b\leqq\mbox{max}\left\{f\left(\dfrac32a-\dfrac12\right),\ f\left(\dfrac32a+\dfrac12\right)\right\}\]
\[\therefore a^2\leqq b\leqq\mbox{max}\left\{\frac32a^2-a+\frac12,\ \frac32a^2+a+\frac12\right\}\]
となります．
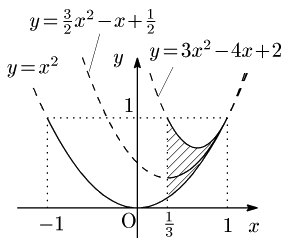
2° $\boldsymbol{\dfrac13\leqq a\leqq 1}$ のとき
$f(p)$ の定義域は $\dfrac32a-\dfrac12\leqq p\leqq1$ となりますから $b=f(p)$ の値域は
\[f(a)\leqq b\leqq\mbox{max}\left\{f\left(\dfrac32a-\dfrac12\right),\ f(1)\right\}\]
\[\therefore a^2\leqq b\leqq\mbox{max}\left\{\frac32a^2-a+\frac12,\ 3a^2-4a+2\right\}\]
となります．
1°，2°，及び対称性により，領域 $D$ と $a,b$ の関係式は答その1と同じになります．
※ max，min の部分の詳しい考え方については，数学Ⅰ 第1章 2次関数 3. 2次関数の最大・最小のスライド，及び【ノート】をご覧ください．
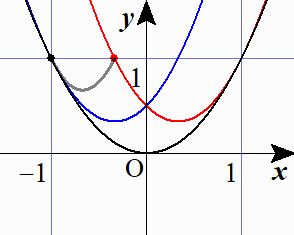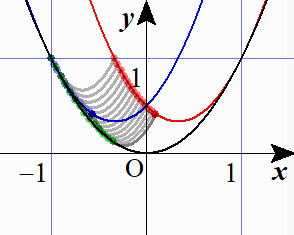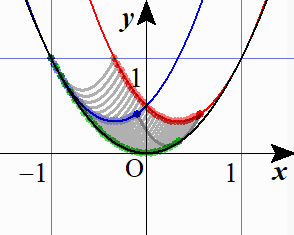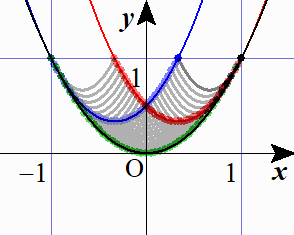
研究～包絡線から捉える～
方程式③ $2p^2-4ap+3a^2-b=0$ を $b=3a^2-4ap+2p^2\ \cdots$(☆) と変形し，この右辺を $a$ の関数とみて $g(a)$ とおくと，$g(a)$ は $ab$ 平面上における下に凸な放物線を表し，加えて放物線 $b=a^2$ と常に $a=p$ で接しています．（実際，(☆)と $b=a^2$ を連立して解くと， $a=p$ を重解にもちます．）つまり曲線群(☆)の包絡線が放物線 $b=a^2$ であるという訳です． 接点の $a$ 座標は，$-1\leqq p\leqq1$ により $-1\leqq a\leqq1$ です。ここで接点の $a$ 座標である $p$ を１つ決めたとき，問題のもう１つの条件である $-1\leqq q\leqq 1$ は，$-1\leqq 3a-2p\leqq 1$ 即ち $\dfrac{2p-1}3\leqq a\leqq \dfrac{2p+1}3$ となりますから，これが放物線(☆)の定義域です． 定義域の両端の値を計算すると
\[\begin{align*} g\left(\frac{2p-1}3\right)&=\frac23p^2+\frac83p+\frac13\ \cdots\mbox{①}\\[5pt] g\left(\frac{2p+1}3\right)&=\frac23p^2-\frac83p+\frac13\ \cdots\mbox{②} \end{align*}\]
となりますが，$p$ のままでは $ab$ 平面上で捉えにくいので，$p=\dfrac32a+\dfrac12$，$\dfrac32a-\dfrac12$ をそれぞれ代入して $a$ の式にしてやると
\[\begin{align*} \mbox{①}&=\frac32a^2+a+\frac12\\[5pt] \mbox{②}&=\frac32a^2-a+\frac12 \end{align*}\]
となります．(結局初めから(☆)に「$p=$」の式を代入したものになっています．）つまり，放物線(☆)の左端が $\dfrac32a^2+a+\dfrac12$ とぶつかるところから，右端が $\dfrac32a^2-a+\dfrac12$ とぶつかるところまでです．このようにして放物線(☆)を包絡線 $b=a^2$ に沿って滑らせていくことで，求める領域が得られます．
包絡線については高校数学ワンポイント19. パラメータが2次で表された直線の通過領域 を参照してください．
このページで疑問は解決されましたか？
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
高校数学ワンポイント
| スライド | ノート | |
| 1. ファクシミリの原理 | [会員] | |
| 2. バウムクーヘン分割 | [会員] | |
| 3. 円と放物線 | ||
| 4. 垂線の長さ | ||
| 5. 不定方程式 | ||
| 6. 関数の連続性は導関数に遺伝するか | ||
| 7. 極方程式における $r$ の正負について | ||
| 8. 極座標表示における扇形分割積分 | ||
| 9. 素因数分解の一意性 | ||
| 10. 三角関数の不定積分 | ||
| 11. コーシー・シュワルツの不等式 | ||
| 12. 放物線と2接線で囲まれた部分の面積 | ||
| 13. 整式の除法(発展編) | ||
| 14. 3次関数のグラフの特徴 | ||
| 15. 曲線の長さを求める公式の証明について | ||
| 16. もう迷わない！必要条件・十分条件のくすっと笑える判定方法 | ||
| 17. 同じものを含む円順列の考え方 | ||
| 18. $f(f(x))=x$ の形をした関数方程式の取り扱い方 | ||
| 19. パラメータが2次で表された直線の通過領域 | ||
| 20. 四面体の面上及び内部を表すベクトル |