垂線の長さ(ノート)

高校数学[総目次]

高校数学ワンポイント

	スライド	ノート
1. ファクシミリの原理	[会員]
2. バウムクーヘン分割	[会員]
3. 円と放物線
4. 垂線の長さ
5. 不定方程式
6. 関数の連続性は導関数に遺伝するか
7. 極方程式における $r$ の正負について
8. 極座標表示における扇形分割積分
9. 素因数分解の一意性
10. 三角関数の不定積分
11. コーシー・シュワルツの不等式
12. 放物線と2接線で囲まれた部分の面積
13. 整式の除法(発展編)
14. 3次関数のグラフの特徴
15. 曲線の長さを求める公式の証明について
16. もう迷わない！必要条件・十分条件のくすっと笑える判定方法
17. 同じものを含む円順列の考え方
18. $f(f(x))=x$ の形をした関数方程式の取り扱い方
19. パラメータが2次で表された直線の通過領域
20. 四面体の面上及び内部を表すベクトル

1．成分が与えられているとき

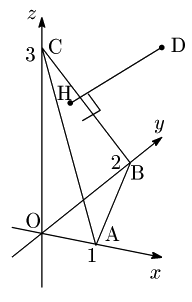
　この問題に対する以下の5つの解法を順に説明します:

お手軽さの順は，軽い方から概ね $$3^\circ,\ 5^\circ > 4^\circ \gg 1^\circ,\ 2^\circ$$ です．

$1^\circ$ $\overrightarrow{\mathstrut{\rm{DH}}}\!= \!r\overrightarrow {\mathstrut{\rm{DA}}} \!+ \!s\overrightarrow{\mathstrut{\rm{DB}}} \!+ \!t\overrightarrow {\mathstrut{\rm{DC}}}$ , $r\!+\!s\!+\!t\!=\!1$とおく

　$\overrightarrow{\mathstrut{\rm{DH}}}=r\overrightarrow{\mathstrut{\rm{DA}}}+s\overrightarrow{\mathstrut{\rm{DB}}}+t\overrightarrow{\mathstrut{\rm{DC}}},\ r+s+t=1\cdots①$ とおきます.
　$\overrightarrow{\mathstrut{\rm{DA}}}=(0,-2,-3),\overrightarrow{\mathstrut{\rm{DB}}}=(-1,0,-3),\overrightarrow{\mathstrut{\rm{DC}}}=(-1,-2,0)$ ですから，

$$\begin{align*} \overrightarrow{\mathstrut{\rm{DH}}}&=r(0,\ -2,\ -3)+s(-1,\ 0,\ -3)+t(-1,\ -2,\ 0)\\[5pt] &=(-s-t, -2r-2t, -3r-3s) \end{align*}$$

です．$\overrightarrow{\mathstrut{\rm{DH}}}\perp\overrightarrow{\mathstrut{\rm{AB}}}$ かつ $\overrightarrow{\mathstrut{\rm{DH}}}\perp\overrightarrow{\mathstrut{\rm{AC}}}$
により，

$$\begin{align*} &(-s-t, -2r-2t, -3r-3s)\cdot(-1,\ 2,\ 0)=0\cdots\mbox{②}\\[5pt] &(-s-t, -2r-2t, -3r-3s)\cdot(-1,\ 0,\ 3)=0\cdots\mbox{③} \end{align*}$$

　①～③ より　$r=-\dfrac{23}{49},\ s=\dfrac{31}{49},\ t=\dfrac{41}{49}$．
　従って $\overrightarrow{\mathstrut{\rm{DH}}}=-\dfrac{12}{49}(6,\ 3,\ 2)$ となりますから，

$${\rm DH}=\left|-\frac{12}{49}\right|\sqrt{6^2+3^2+2^2}=\bf{\frac{12}7}$$

$2^\circ$ $\overrightarrow {\mathstrut{\rm{DH}}}\!= \!\overrightarrow{\mathstrut{\rm{DA}}} \!+ \!s\overrightarrow {\mathstrut{\rm{AB}}} \!+ \!t\overrightarrow {\mathstrut{\rm{AC}}}$ とおく

　$\overrightarrow{\mathstrut{\rm{DH}}}=\overrightarrow{\mathstrut{\rm{DA}}}+s\overrightarrow{\mathstrut{\rm{AB}}}+t\overrightarrow{\mathstrut{\rm{AC}}}$ とおきます．
　$\overrightarrow{\mathstrut{\rm{DA}}}=(0,-2,-3),\ \overrightarrow{\mathstrut{\rm{AB}}}=(-1,2,0),\ \overrightarrow{\mathstrut{\rm{AC}}}=(-1,0,3)$ ですから， $$\begin{align*} \overrightarrow{\mathstrut{\rm{DH}}}&=(0,\ -2,\ -3)+s(-1,\ 2,\ 0)+t(-1,\ 0,\ 3)\\[5pt] &=(-s-t,\ -2+2s,\ -3+3t) \end{align*}$$ です．　$\overrightarrow{\mathstrut{\rm{DH}}}\perp\overrightarrow{\mathstrut{\rm{AB}}}$ かつ $\overrightarrow{\mathstrut{\rm{DH}}}\perp\overrightarrow{\mathstrut{\rm{AC}}}$ により， $$\begin{align*} &(-s-t,\ -2+2s,\ -3+3t)\cdot(-1,\ 2,\ 0)=0\cdots\mbox{①}\\[5pt] &(-s-t,\ -2+2s,\ -3+3t)\cdot(-1,\ 0,\ 3)=0\cdots\mbox{②} \end{align*}$$ 　①，②より　$s=\dfrac{31}{49},\ t=\dfrac{41}{49}$．
　従って $\overrightarrow{\mathstrut{\rm{DH}}}=-\dfrac{12}{49}(6,\ 3,\ 2)$ となりますから， $${\rm DH}=\left|-\frac{12}{49}\right|\sqrt{6^2+3^2+2^2}=\bf{\frac{12}7}$$

補足

　上の解答のようにして $s$ と $t$ を求めておいたのち，$\overrightarrow{\rm{DH}}$ の大きさを求める際には次のようにしてもよいでしょう：

$$\begin{align*} |\overrightarrow{\rm{DH}}|^2&=\overrightarrow{\rm{DH}}\cdot\overrightarrow{\rm{DH}}\\[5pt] &=\overrightarrow{\rm{DH}}\cdot\bigl(\overrightarrow{\rm{DA}}+\frac{31}{49}\overrightarrow{\rm{AB}}+\frac{41}{49}\overrightarrow{\rm{AC}}\bigr)\\[5pt] &=\overrightarrow{\rm{DH}}\cdot\overrightarrow{\rm{DA}}\ \ (\because \overrightarrow{\rm{DH}}\perp\overrightarrow{\rm{AB}},\ \overrightarrow{\rm{DH}}\perp\overrightarrow{\rm{AC}})\\[5pt] &=-\frac{12}{49}(6,\ 3,\ 2)\cdot(0,\ -2,\ -3)\\[5pt] &=\frac{12^2}{49}\\[8pt] \therefore |\overrightarrow{\rm{DH}}|&={\bf \frac{12}7} \end{align*}$$

　この $\overrightarrow{\rm{DH}}$ の一方だけを残して計算するという方法は，ベクトルの成分が与えられていない場合に極めて有効です．

$3^\circ$ 正射影ベクトルの利用

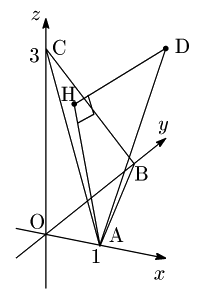
　$\overrightarrow{\mathstrut{\rm{AB}}}$ と $\overrightarrow{\mathstrut{\rm{AC}}}$ の双方に垂直なベクトルの 1 つとして
$\overrightarrow{\mathstrut{n}}=(6,\ 3,\ 2)$ がとれます．実際，

$$\begin{align*} \overrightarrow{\rm{AB}}\cdot\overrightarrow{\mathstrut{n}}&=(-1,\ 2,\ 0)\cdot(6,\ 3,\ 2)\\[5pt] &=-6+6+0=0\\[5pt] \overrightarrow{\rm{AC}}\cdot\overrightarrow{\mathstrut{n}}&=(-1,\ 0,\ 3)\cdot(6,\ 3,\ 2)\\[5pt] &=-6+0+6=0\\[5pt] \end{align*}$$

です．$\overrightarrow{\mathstrut{\rm{DH}}}$ は(例えば) $\overrightarrow{\mathstrut{\rm{DA}}}$ の $\overrightarrow{\mathstrut{n}}$ への正射影ベクトルですから，

$$\begin{align*} |\overrightarrow{\mathstrut{\rm{DH}}}|&=\left|\frac{\overrightarrow{\mathstrut{\rm{DA}}}\cdot\overrightarrow{\mathstrut{n}}}{|\overrightarrow{\mathstrut{n}}|^2}\overrightarrow{\mathstrut{n}}\right| =\frac{|\overrightarrow{\mathstrut{\rm{DA}}}\cdot\overrightarrow{\mathstrut{n}}|}{|\overrightarrow{\mathstrut{n}}|}\\[10pt] &=\frac{|(0,-2,-3)\cdot(6,3,2)|}{\sqrt{6^2+3^2+2^2}}=\bf{\frac{12}7} \end{align*}$$

補足

　正射影ベクトルの詳しい考え方については，数学B 第1章 ベクトル 4.ベクトルの内積(会員向け)，及び【ノート】をご覧ください．

$4^\circ$ 点$\rm D$を通る直線の方程式を利用

　$\overrightarrow{\mathstrut{\rm{AB}}}$ と $\overrightarrow{\mathstrut{\rm{AC}}}$ の双方に垂直なベクトルの 1 つとして
$\overrightarrow{\mathstrut{n}}=(6,\ 3,\ 2)$ がとれます($\to 3^\circ$ 参照)．点 D を通り，方向ベクトルが $\overrightarrow{\mathstrut{n}}$ である直線の方程式は

$$\begin{align*} (x,\ y,\ z)&=\overrightarrow{\mathstrut{\rm{OD}}}+t\overrightarrow{\mathstrut{n}}\\[5pt] &=(1,\ 2,\ 3)+t(6,\ 3,\ 2)\\[5pt] &=(1+6t,\ 2+3t,\ 3+2t)\ \ \cdots\mbox{①} \end{align*}$$

　また，平面 ABC の方程式は

$$\begin{gather*} 6(x-1)+3(y-0)+2(z-0)=0\\[5pt] \therefore\ \ 6x+3y+2z-6=0\ \cdots\mbox{②} \end{gather*}$$

　H は直線と平面の交点ですから，①を②に代入して，

$$\begin{gather*} 6(1+6t)+3(2+3t)+2(3+2t)-6=0\\[5pt] \therefore t=-\frac{12}{49} \end{gather*}$$

　従って， $$\overrightarrow{\mathstrut{\rm{OH}}}=(1,\ 2,\ 3)-\frac{12}{49}(6,\ 3,\ 2)$$ となります．よって，

$$\begin{align*} |\overrightarrow{\mathstrut{\rm{DH}}}|&=|\overrightarrow{\mathstrut{\rm{OH}}}-\overrightarrow{\mathstrut{\rm{OD}}}|\\[5pt] &=\left|\left\{(1,\ 2,\ 3)-\frac{12}{49}(6,\ 3,\ 2)\right\}-(1,\ 2,\ 3)\right|\\[5pt] &=\left|-\frac{12}{49}(6, 3, 2)\right|=\bf{\frac{12}7} \end{align*}$$

$5^\circ$ 点と平面の距離の公式を利用

　点 D$(1,\ 2,\ 3)$ と平面 ABC： $6x+3y+2z-6=0$（$\to 4^\circ$の②式参照）の距離は，公式により $$\rm{DH}=\frac{|6\cdot 1+3\cdot 2+3\cdot 2-6|}{\sqrt{6^2+3^2+2^2}}=\bf{\frac{12}7}$$

2．成分が与えられていないとき

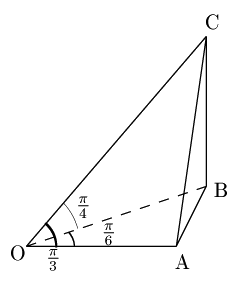
答

　まず $\overrightarrow{\rm CH}$ を，上の方針2に従って計算します．
　$\overrightarrow{\rm OA}=\overrightarrow{\mathstrut{a}},\ \overrightarrow{\rm OB}=\overrightarrow{\mathstrut{b}},\ \overrightarrow{\rm OC}=\overrightarrow{\mathstrut{c}}$ とおきます．

$$\begin{align*} \overrightarrow{\mathstrut{a}}\cdot\overrightarrow{\mathstrut{b}}&=\frac{\sqrt3}2\\[5pt] \overrightarrow{\mathstrut{b}}\cdot\overrightarrow{\mathstrut{c}}&=\frac{\sqrt2}2\\[5pt] \overrightarrow{\mathstrut{c}}\cdot\overrightarrow{\mathstrut{a}}&=\frac12\\[5pt] \end{align*}$$

ですから，$\overrightarrow{\rm OH}=s\overrightarrow{\mathstrut{a}}+t\overrightarrow{\mathstrut{b}}$ とおくと，

$$\begin{align*} \overrightarrow{\rm CH}\perp\overrightarrow{\mathstrut{a}}&\iff(s\overrightarrow{\mathstrut{a}}+t\overrightarrow{\mathstrut{b}}-\overrightarrow{\mathstrut{c}})\cdot\overrightarrow{\mathstrut{a}}=0\\[5pt] \overrightarrow{\rm CH}\perp\overrightarrow{\mathstrut{b}}&\iff(s\overrightarrow{\mathstrut{a}}+t\overrightarrow{\mathstrut{b}}-\overrightarrow{\mathstrut{c}})\cdot\overrightarrow{\mathstrut{b}}=0 \end{align*}$$ $$\therefore\left\{ \begin{array}{l} s+\dfrac{\sqrt 3}2t-\dfrac12=0\\[5pt] \dfrac{\sqrt 3}2s+t-\dfrac{\sqrt2}2=0 \end{array}\right.$$

　これを解いて，$s=2-\sqrt6,\ t=2\sqrt2-\sqrt3$ を得ます．よって，

$$\overrightarrow{\rm CH}=(2-\sqrt6)\overrightarrow{\mathstrut{a}}+(2\sqrt2-\sqrt3)\overrightarrow{\mathstrut{b}}-\overrightarrow{\mathstrut{c}}$$

です．
　ここで $\overrightarrow{\rm CH}$ の大きさを，

$$|\overrightarrow{\rm CH}|^2=\left|(2-\sqrt6)\overrightarrow{\mathstrut{a}}+(2\sqrt2-\sqrt3)\overrightarrow{\mathstrut{b}}-\overrightarrow{\mathstrut{c}}\right|^2$$

としては計算が大変です．この煩雑さを回避するのが上の方針2の補足で示した方法です．$\overrightarrow{\rm CH}\perp\overrightarrow{\mathstrut{a}},\ \overrightarrow{\rm CH}\perp\overrightarrow{\mathstrut{b}}$ に注意すると，

$$\begin{align*} |\overrightarrow{\rm CH}|^2&=\overrightarrow{\rm CH}\cdot\overrightarrow{\rm CH}\\[5pt] &=\overrightarrow{\rm CH}\cdot\{(2-\sqrt6)\overrightarrow{\mathstrut{a}}+(2\sqrt2-\sqrt3)\overrightarrow{\mathstrut{b}}-\overrightarrow{\mathstrut{c}}\}\\[5pt] &=-\overrightarrow{\rm CH}\cdot\overrightarrow{\mathstrut{c}}\ \ \ \ (\leftarrow\mbox{ここがポイント！})\\[5pt] &=-\{(2-\sqrt6)\overrightarrow{\mathstrut{a}}+(2\sqrt2-\sqrt3)\overrightarrow{\mathstrut{b}}-\overrightarrow{\mathstrut{c}}\}\cdot\overrightarrow{\mathstrut{c}}\\[5pt] &=-\left\{(2-\sqrt6)\cdot\frac12+(2\sqrt2-\sqrt3)\cdot\frac{\sqrt2}2-1\right\}\\[5pt] &=\sqrt6-2 \end{align*}$$

　$|\overrightarrow{\rm CH}|\geqq0$ ですから，
$$|\overrightarrow{\rm CH}|=\sqrt{\sqrt6-2}$$
となります．

---

高校数学[総目次]

高校数学ワンポイント

	スライド	ノート
1. ファクシミリの原理	[会員]
2. バウムクーヘン分割	[会員]
3. 円と放物線
4. 垂線の長さ
5. 不定方程式
6. 関数の連続性は導関数に遺伝するか
7. 極方程式における $r$ の正負について
8. 極座標表示における扇形分割積分
9. 素因数分解の一意性
10. 三角関数の不定積分
11. コーシー・シュワルツの不等式
12. 放物線と2接線で囲まれた部分の面積
13. 整式の除法(発展編)
14. 3次関数のグラフの特徴
15. 曲線の長さを求める公式の証明について
16. もう迷わない！必要条件・十分条件のくすっと笑える判定方法
17. 同じものを含む円順列の考え方
18. $f(f(x))=x$ の形をした関数方程式の取り扱い方
19. パラメータが2次で表された直線の通過領域
20. 四面体の面上及び内部を表すベクトル