高校数学[総目次]
高校数学ワンポイント
| スライド | ノート | |
| 1. ファクシミリの原理 | [会員] | |
| 2. バウムクーヘン分割 | [会員] | |
| 3. 円と放物線 | ||
| 4. 垂線の長さ | ||
| 5. 不定方程式 | ||
| 6. 関数の連続性は導関数に遺伝するか | ||
| 7. 極方程式における $r$ の正負について | ||
| 8. 極座標表示における扇形分割積分 | ||
| 9. 素因数分解の一意性 | ||
| 10. 三角関数の不定積分 | ||
| 11. シュワルツの不等式 | ||
| 12. 放物線と2接線で囲まれた部分の面積 | ||
| 13. 整式の除法(発展編) | ||
| 14. 3次関数のグラフの特徴 | ||
| 15. 曲線の長さを求める公式の証明について | ||
| 16. もう迷わない!必要条件・十分条件の判定方法 |
12. 放物線と2接線で囲まれた部分の面積
1.よくある例題
次は教科書によくある例題と答えです.
例題 $y=x^2$ 上の2点 $(-1,1)$,$(3,9)$ における2本の接線とこの放物線で囲まれた部分の面積 $S$ を求めよ.
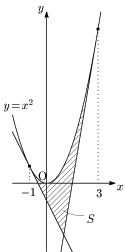
答
$y’=2x$ より,題意の2本の接線の方程式は
\[\begin{align*} &y-1=-2(x+1),\\[5pt] &y-9=6(x-3). \end{align*}\]
です.整理して
\[y=-2x-1,\ y=6x-9.\]
2接線の交点の $x$ 座標は,$y$ を消去した方程式
\[-2x-1=6x-9\]
を解いて,$x=1$ となります.
従って求める面積 $S$ はグラフの上下関係を考えて,
\[\begin{align*} S&=\int_{-1}^1\!\!\{x^2-(-2x-1)\}dx+\int_1^3\!\!\{x^2-(6x-9)\}dx\\[5pt] &=\int_{-1}^1\!\!(x+1)^2dx+\int_1^3\!\!(x-3)^2dx\\[5pt] &=\left[\frac{(x+1)^3}3\right]_{-1}^1+\left[\frac{(x-3)^3}3\right]_1^3\\[5pt] &=\frac83+\frac83\\[5pt] &=\boldsymbol{\frac{16}3} \end{align*}\]
となります.
※ 最後の定積分を計算するところで,数学Ⅲで出てくる こちら の公式を使いましたが,数学Ⅲを学ばない文系の人たちにもぜひ使えるようになってほしい公式です.
今得られた結果と計算過程から次のことがわかります.
① 2接線の交点の $\boldsymbol{x}$ 座標は,2接点の $\boldsymbol{x}$ 座標の平均である:
\[\frac{-1+3}2=1\]
② 直線 $\boldsymbol{x=1}$ で分けた左右の面積はともに等しく$\boldsymbol{\dfrac83}$ である.
更に,2つの接点を通る直線の方程式を $y=l(x)$ とすると,この直線と放物線で囲まれた部分の面積 $T$ が
\[\begin{align*} T&=\int_{-1}^3\!\{l(x)-x^2\}dx\\[5pt] &=-\int_{-1}^3(x+1)(x-3)dx\\[5pt] &=-\left\{-\frac{(3+1)^3}6\right\}\\[5pt] &=\frac{32}3 \end{align*}\]
となりますから,先ほど求めた面積を $S$ とすると,
\[S:T=\frac{16}3:\frac{32}3\]
即ち
③ $\boldsymbol{ S:T=1:2}$ である.
ということがいえます.
2.一般論
実は先ほど見た結果は,任意の放物線と,任意の2接線について,いつでも成り立つことなのです.
① $p=\dfrac{\alpha+\beta}2$ である.
② $S_1=S_2$ である.
③ $(S_1+S_2):S_3=1:2$ である.
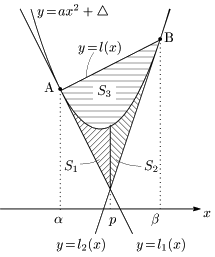
証明
① $\boldsymbol{p=\dfrac{\alpha+\beta}2}$ である.
$\alpha$ は2次方程式 $f(x)=l_1(x)$ の重解で,$\beta$ は2次方程式 $f(x)=l_2(x)$ の重解になっていますから,
\[\begin{align*} &f(x)-l_1(x)=a(x-\alpha)^2,\\[5pt] &f(x)-l_2(x)=a(x-\beta)^2 \end{align*}\]
と変形できます.両辺の $x$ を $p$ とおくと,
$f(p)-l_1(p)=a(p-\alpha)^2\ \ \cdots$①
$f(p)-l_2(p)=a(p-\beta)^2\ \ \cdots$②
$l_1(p)=l_2(p)$ であることに注意して,①$-$②より
\[0=a\{(p-\alpha)^2-(p-\beta)^2\}\]
両辺を入れ替えて計算すると,
\[a(2p-\alpha-\beta)(-\alpha+\beta)=0\]
※ 因数分解の公式 $A^2-B^2=(A+B)(A-B)$ を利用しました.
$a>0$,及び $\alpha\neq\beta$ より $-\alpha+\beta\neq0$ ですから,
\[2p-\alpha-\beta=0\]
\[\therefore p=\frac{\alpha+\beta}2.\]
② $\boldsymbol{S_1=S_2}$ である.
\[\begin{align*} S_1&=\int_\alpha^p\{f(x)-l_1(x)\}dx\\[5pt] &=a\int_\alpha^p(x-\alpha)^2dx\\[5pt] &=a\left[\frac{(x-\alpha)^3}3\right]_\alpha^p\\[5pt] &=\frac a3(p-\alpha)^3\\ &=\frac a3\left\{\frac{\alpha+\beta}2-\alpha\right\}^3\\[5pt] &=\frac a3\left(\frac{\beta-\alpha}2\right)^3\\[5pt] &=\frac{a(\beta-\alpha)^3}{24} \end{align*}\]
また $S_2$ の方は,
\[\begin{align*} S_2&=\int_p^\beta\{f(x)-l_2(x)\}dx\\[5pt] &=a\int_p^\beta(x-\beta)^2dx\\[5pt] &=a\left[\frac{(x-\beta)^3}3\right]_p^\beta\\[5pt] &=-\frac a3(p-\beta)^3\\ &=-\frac a3\left\{\frac{\alpha+\beta}2-\beta\right\}^3\\[5pt] &=-\frac a3\left(-\frac{\beta-\alpha}2\right)^3\\[5pt] &=\frac{a(\beta-\alpha)^3}{24} \end{align*}\]
よって,$S_1=S_2$.
③ $\boldsymbol{(S_1+S_2):S_3=1:2}$ である.
直線ABの方程式を $y=l(x)$ とすると,
\[\begin{align*} S_3&=\int_\alpha^\beta\{l(x)-f(x)\}dx\\[5pt] &=-a\int_\alpha^\beta(x-\alpha)(x-\beta)dx\\[5pt] &=-a\left\{-\frac{(\beta-\alpha)^3}6\right\}\\[5pt] &=\frac{a(\beta-\alpha)^3}6 \end{align*}\]
よって,
\[\begin{align*} (S_1+S_2):S_3&=\frac{a(\beta-\alpha)^3}{24}\times 2:\frac{a(\beta-\alpha)^3}6\\[5pt] &=\frac{a(\beta-\alpha)^3}{12}:\frac{a(\beta-\alpha)^3}6\\[5pt] &=1:2 \end{align*}\]
■
3.等積変形による証明
Section 2 では3つの性質を式によって証明しましたが,①と②の性質は等積変形による幾何的な証明も明快です.
今,放物線 $y=f(x)$,及び2接線 $y=l_1(x)$,$y=l_2(x)$ に対して,3つの関数 $f(x),\ l_1(x),\ l_2(x)$ から直線ABを表す関数 $l(x)$ を一斉に引いた関数を考えます:
\[\begin{align*} y=f(x)&-l(x)\\[5pt] y=l_1(x)&-l(x)\\[5pt] y=l_2(x)&-l(x) \end{align*}\]
$l(x)$が1次以下の関数ですから,これらのグラフは順に
放物線,直線,直線
になります.さてこれらはどのような放物線や直線でしょうか.実は次のような図形になります.
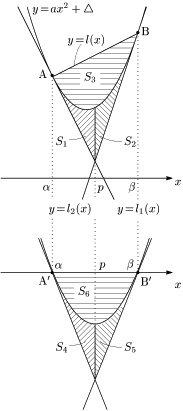
下が $l(x)$ を減じた図
この「直線ABを表す関数 $l(x)$ を減ずる」という操作は,直線ABを $x$ 軸に移すような変換を意味します.そして次が重要なのですが,この変換において,囲まれた部分の面積が変わらないのです.つまりこの変換は等積変形です.実際,
\[\begin{align*} S_4&=\int_\alpha^p\{(f-l)-(l_1-l)\}dx=\int_\alpha^p(f-l_1)dx=S_1\\[5pt] S_5&=\int_p^\beta\{(f-l)-(l_2-l)\}dx=\int_p^\beta(f-l_2)dx=S_2\\[5pt] S_6&=-\int_\alpha^\beta \{f-l\}dx=\int_\alpha^\beta \{l-f\}dx=S_3\\[5pt] \end{align*}\]
※ $f(x)$ などの「$(x)$」を省略しました.
となっています.
放物線は軸に関して対称ですから,$p$ が $\alpha$ と $\beta$ の平均であることや $S_4=S_5$ 即ち $S_1=S_2$ は図から明らかです.
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
高校数学ワンポイント
| スライド | ノート | |
| 1. ファクシミリの原理 | [会員] | |
| 2. バウムクーヘン分割 | [会員] | |
| 3. 円と放物線 | ||
| 4. 垂線の長さ | ||
| 5. 不定方程式 | ||
| 6. 関数の連続性は導関数に遺伝するか | ||
| 7. 極方程式における $r$ の正負について | ||
| 8. 極座標表示における扇形分割積分 | ||
| 9. 素因数分解の一意性 | ||
| 10. 三角関数の不定積分 | ||
| 11. シュワルツの不等式 | ||
| 12. 放物線と2接線で囲まれた部分の面積 | ||
| 13. 整式の除法(発展編) | ||
| 14. 3次関数のグラフの特徴 | ||
| 15. 曲線の長さを求める公式の証明について | ||
| 16. もう迷わない!必要条件・十分条件の判定方法 |
