2. 置換積分法(不定積分)(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅲ　第3章　積分法

	スライド	ノート
1. 不定積分	[無料]
2. 置換積分法（不定積分）	[無料]
3. 部分積分法（不定積分）	[無料]
4. 定積分とその性質	[会員]
5. 置換積分法（定積分）	[会員]
6. 部分積分法（定積分）	[会員]
7. 定積分と微分法	[会員]
8. 定積分と和の極限	[会員]
9. 定積分と不等式	[会員]
10. 定積分の応用（面積）	[会員]
11. 定積分の応用（体積）	[会員]
12. 定積分の応用（回転体の体積）	[会員]
13. 曲線の長さ

2．置換積分法(不定積分)

2.1　$\displaystyle\int\!f(ax+b)dx$ の計算

まずは置換積分法の特別な形から

　$F(x)$ を関数 $f(x)$ の不定積分の1つとする．$\bigl(F'(x)=f(x)\bigr)$
　このとき， \[\{F(ax+b)\}’=F'(ax+b)\cdot a=af(ax+b)\] \[\therefore f(ax+b)=\left\{\frac1aF(ax+b)\right\}’\] 　よって，$\dfrac1aF(ax+b)$ は $f(ax+b)$ の不定積分であるから次が成り立つ：

\[ \int\!f(ax+b)dx=\frac1aF(ax+b)+C\ \cdots(*)\]

補足

　$ax+b=u$ とおくと，$(*)$ は \[\int\!f(u)dx=\frac1{u’}F(u)+C\]

例1　$\displaystyle\int\!(ax+b)^ndx$

　$\left\{\begin{array}{l} f(u)=u^n\\ u=ax+b \end{array}\right.$ とおくと， \[\begin{align*} \mbox{与式}&=\frac1{u’}\cdot F(u)+C\\[5pt] &=\frac1a\cdot\frac{u^{n+1}}{n+1}+C\\[5pt] &=\underline{\frac1{a(n+1)}(ax+b)^{n+1}+C} \end{align*}\]

　特に $a=1$ の場合の次の式は，数学Ⅲを学ばない文系の人たちにも是非使えるようになっておいてほしい．計算スピードと正確性が劇的に向上するので必須の公式としておきたい：

例2　$\displaystyle\int\!\cos(2x+3)dx$

　$\left\{\begin{array}{l} f(u)=\cos u\\ u=2x+3 \end{array}\right.$ とおくと， \[\begin{align*} \mbox{与式}&=\frac1{u’}\cdot F(u)+C\\[5pt] &=\frac12\sin u+C\\[5pt] &=\underline{\frac12\sin(2x+3)+C} \end{align*}\]

例3　$\displaystyle\int\!2e^{-3x+4}dx$

　$\left\{\begin{array}{l} f(u)=2e^u\\ u=-3x+4 \end{array}\right.$とおくと， \[\begin{align*} \mbox{与式}&=\frac1{u’}\cdot F(u)+C\\[5pt] &=\frac1{-3} 2e^u+C\\[5pt] &=\underline{-\frac23 e^{-3x+4}+C} \end{align*}\]

2.2　置換積分法

置換積分法の具体例

　積分変数を別の変数に変換(置換)する積分方法を，置換積分法という．置換積分法によって，積分変数を別なものに変えることで，積分できなかった関数が積分できるようになることがある．

例題　次の不定積分を求めよ． \[y=\int\!\sqrt x\,dx\ \ \cdots\mbox{①}\]

やり方その1

\[y=\int\!x^{\frac12}dx=\frac23x^{\frac32}+C=\underline{\frac23x\sqrt x+C}\]

やり方その2

　$\sqrt x=t\ \cdots$② とおく．このとき \[x=t^2\hspace{10mm} \therefore\dfrac{dx}{dt}=2t\ \cdots\mbox{③}\] である．合成関数の導関数により， \[\begin{align*} \frac{dy}{dt}&=\frac{dy}{dx}\cdot\frac{dx}{dt}\\[5pt] &=\sqrt x\cdot 2t\ \ \ (\because \mbox{①，③})\\[5pt] &=t\cdot 2t\ \ \ (\because \mbox{②}) \end{align*}\] \[\therefore \frac{dy}{dt}=t\cdot2t\] 　これは「$y$ を $t$ で微分すると $t\cdot2t$ になる」ことを意味するから， \[\begin{align*} y&=\int t\cdot2t\,dt\ \cdots\mbox{④}\\[5pt] &=\int 2t^2\,dt\\[5pt] &=\frac23t^3+C\\[5pt] &=\underline{\frac23x\sqrt x+C}\ \ \ (\because\mbox{②}) \end{align*}\]

　さて，①と④を比較してみよう：

\[\begin{align*} &y=\int\!\sqrt x\,dx\ \ \cdots\mbox{①}\\[5pt] &y=\int t\cdot2tdt\ \ \cdots\mbox{④} \end{align*}\]

　④は①に②を代入し，③を形式的に（つまり $\dfrac{dy}{dt}$ を分数とみなして）$dx=2tdt$ と変形し，①に代入したものとなっている．

　「やり方その2」はもともと $x$ であった積分変数を，$t$ に変換して積分を計算しやすくした．このように積分変数を変換して積分する方法を置換積分法という．

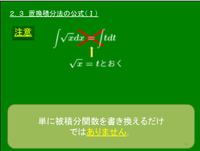
2.3 置換積分法の公式(Ⅰ)

置換積分法の一般論

　一般に $y=\displaystyle\int\!f(x)dx$ において，$x$ が微分可能な $t$ の関数 $g(t)$ で $x=g(t)$ と表されているとすると， \[\frac{dy}{dt}=\frac{dy}{dx}\cdot\frac{dx}{dt}=f(x)g'(t)=f(g(t))g'(t)\] 　これは「$y$ を $t$ で微分すると $f(g(t))g'(t)$ になる」ことを意味するから， \[y=\int\!f(g(t))g'(t)\,dt\] 　一方，$y=\displaystyle\int\!f(x)dx$ であったから次を得る：

置換積分法の公式(I) \[ \int \!\! f(x)dx=\int\!\! f\bigl(g(t)\bigr)g'(t)\,dt\ \ \ (\mbox{ただし，}x=g(t)\ )\]

注意

置換積分法では単に変数の置き換えだけではダメ

　上の例からわかるように，一般には $\sqrt x=t$ とおいたとき， \[\int\!\sqrt x\,dx=\int\!t\,dt\] にはならない．( $g'(t)=2t$ が付け加わる．)

補足

① 上の例で $\sqrt x=t$ とおいたように，実際には $x=g(t)$ とおくよりも，$h(x)=t$ のようにすることが多い．
② 置換積分法の公式(Ⅰ)をみると， \[\begin{align*} y&=\int\!f(x)\ \underline{dx}\\[5pt] &=\int\!f(x)\,\underline{g'(t)dt} \end{align*}\] であり，$dx$ が $g'(t)dt$ に置き換わっただけだが，これは $x=g(t)$ の両辺を $t$ で微分して $\dfrac{dx}{dt}=g'(t)$ としたものを形式的に $dx=g'(t)dt$ として代入したものとなっている．

2.4 置換積分法の公式(Ⅱ)

この公式が自然と使えるようになれば上級者

　置換積分法の公式(Ⅰ)において，左辺と右辺を入れ替え，更に $x$ と $t$ も入れ替えると，次の公式が得られる：

置換積分法の公式(II) \[ \int\!\! f\bigl( g(x) \bigr)g'(x)dx=\int\!\! f(t)dt\ \ \ (\mbox{ただし，}g(x)=t) \]

　要は被積分関数が $f(g(x))g'(x)$ の形になっていることをいかに見抜くかである．見抜けた人とそうでない人では積分のスピードと正確性が大きく異なり，当然前者が優位に立つ．ただ見抜けるようになるまでにはある程度の訓練と慣れが必要で，この公式が自然に使えるようになったならば置換積分法の上級者といってよいであろう．

例1

$\displaystyle\int\!\sin^2x\cos x\,dx=\int\!\sin^2x\cdot(\sin x)’\,dx\ \ \cdots$ ①

　ここで， $\left\{\begin{array}{l} f(t)=t^2\\ t=\sin x(\,=g(x)\,) \end{array}\right.$ とみると， \[\begin{align*} \mbox{①}&=\int\!f(t)\,dt\\[5pt] &=\int\!t^2\,dt\\[5pt] &=\frac13t^3+C\\[5pt] &=\underline{\frac13\sin^3x+C} \end{align*}\]

例2

$\displaystyle\int\!\frac{\log x}x dx=\int\!\log x\cdot(\log x)’\,dx\ \ \cdots$ ②

　ここで， $\left\{\begin{array}{l} f(t)=t\\ t=\log x(\,=g(x)\,) \end{array}\right.$ とみると， \[\begin{align*} \mbox{②}&=\int\!f(t)\,dt\\[5pt] &=\int\!t\,dt\\[5pt] &=\frac12t^2+C\\[5pt] &=\underline{\frac12(\log x)^2+C} \end{align*}\]

2.5 $\displaystyle\int\!\frac{g'(x)}{g(x)}dx$ の積分

置換積分法の公式(Ⅱ)の特別な形

　置換積分法の公式(Ⅱ)において，特に $f(t)=\dfrac1t$ のときは， \[\begin{align*} \int\!\frac{g'(x)}{g(x)}dx&=\int\!\frac{dt}t\\[5pt] &=\log|t|+C\\[5pt] &=\log|g(x)|+C \end{align*}\] となるから，次を得る：

例1

\[\begin{align*} \int\!\frac{2x+1}{x^2+x+1}dx&=\frac{(x^2+x+1)’}{x^2+x+1}dx\\[5pt] &=\log|x^2+x+1|+C\\[5pt] &=\underline{\log(x^2+x+1)+C} \end{align*}\] \[\left(\because x^2+x+1=\left(x+\frac12\right)^2+\frac34>0\right)\]

例2

\[\begin{align*} \int\!\tan x\,dx&=\frac{\sin x}{\cos x}dx\\[5pt] &=-\int\!\frac{(\cos x)’}{\cos x}dx\\[5pt] &=\underline{-\log|\cos x|+C} \end{align*}\]

補足

　三角関数の不定積分が出揃ったので，まとめると次のようになる：

三角関数の不定積分 \[\begin{align*} \int\!\sin x\,dx&=-\cos x+C\\[5pt] \int\!\cos x\,dx&=\sin x+C\\[5pt] \int\!\tan x\,dx&=-\log|\cos x| +C \end{align*}\]

---

高校数学[総目次]

数学Ⅲ　第3章　積分法

	スライド	ノート
1. 不定積分	[無料]
2. 置換積分法（不定積分）	[無料]
3. 部分積分法（不定積分）	[無料]
4. 定積分とその性質	[会員]
5. 置換積分法（定積分）	[会員]
6. 部分積分法（定積分）	[会員]
7. 定積分と微分法	[会員]
8. 定積分と和の極限	[会員]
9. 定積分と不等式	[会員]
10. 定積分の応用（面積）	[会員]
11. 定積分の応用（体積）	[会員]
12. 定積分の応用（回転体の体積）	[会員]
13. 曲線の長さ