9. 定積分と不等式(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅲ　第3章　積分法

	スライド	ノート
1. 不定積分	[無料]
2. 置換積分法（不定積分）	[無料]
3. 部分積分法（不定積分）	[無料]
4. 定積分とその性質	[会員]
5. 置換積分法（定積分）	[会員]
6. 部分積分法（定積分）	[会員]
7. 定積分と微分法	[会員]
8. 定積分と和の極限	[会員]
9. 定積分と不等式	[会員]
10. 定積分の応用（面積）	[会員]
11. 定積分の応用（体積）	[会員]
12. 定積分の応用（回転体の体積）	[会員]
13. 曲線の長さ

9．定積分と不等式

9.1　定積分と不等式

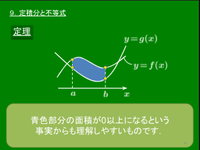
定理 　閉区間 $[a,b]$ で連続な関数 $f(x)$ が，この区間で常に $f(x)\geqq0$ ならば， \[\int_a^b\!\!f(x)\,dx\geqq0\] が成り立つ．等号成立は，$[a,b]$ で常に $f(x)=0$ のとき．

証明

　$\displaystyle{F(x)=\int_a^x\!\!f(t)dt}$ とする．$F(b)\geqq 0$ を示せばよい． \[F'(x)=\frac d{dx}\int_a^x\!\!f(t)dt=f(x)\geqq 0\ \ （\because \mbox{仮定})\] であるから，$F(x)$ は $a\leqq x\leqq b$ で単調に増加する関数である．よって， \[F(x)\geqq F(a)\left(=\int_a^a\!\!f(t)dt\right)=0\] により， $F(x)$ は $a\leqq x\leqq b$ で常に非負となり，従って $F(b)\geqq 0$． また，等号が成立するとき，すなわち $\displaystyle{\int_a^b\!f(x)dx=F(b)=0}$ が成り立つときは，$F(x)$ の単調増加性により \[0=F(a)\leqq F(x)\leqq F(b)=0\]となるから，$F(x)$ は $a\leqq x\leqq b$ で常に0． 故に $f(x)=F'(x)=(0)’=0$．

■

系 　閉区間 $[a,b]$ で連続な関数 $f(x)$ が，この区間で常に $f(x)\geqq 0$，かつ $\displaystyle{\int_a^b\!f(x)dx= 0}$ ならば，この区間で常に $f(x)=0$．

証明

　上の定理の証明における等号成立時の議論により明らか．

■

　上の定理から，直ちに次が成り立つ：

定理 　閉区間 $[a,b]$ で連続な関数 $f(x)$ が，この区間で常に $f(x)\geqq g(x)$ ならば， \[\int_a^b\!\!f(x)\,dx\geqq\int_a^b\!\!g(x)\,dx\] が成り立つ．等号成立は，$[a,b]$ で常に $f(x)=g(x)$ のとき．

証明

　$F(x)=f(x)-g(x)$ とおくと，区間 $[a,b]$ で常に $F(x)\geqq0$．従って， \[\int_a^b\!\!F(x)\,dx=\int_a^b\!\!\{f(x)-g(x)\}dx\geqq0\] \[\therefore \int_a^b\!\!f(x)\,dx-\int_a^b\!\!g(x)\,dx\geqq0\] \[\therefore \int_a^b\!\!f(x)\,dx\geqq\int_a^b\!\!g(x)\,dx\]

■

例題1　次を示せ． \[\frac\pi4 < \int_0^1\!\!\frac{dx}{1+x^3} < 1\]

証明
　閉区間 $[0,1]$ において，常に \[1 \leqq 1+x^3\leqq 1+x^2 \] であるから， \[\frac1{1+x^2}\leqq\frac1{1+x^3}\leqq 1\] 　各辺を0から1まで積分して， \[\int_0^1\!\!\frac{dx}{1+x^2} < \int_0^1\!\!\frac{dx}{1+x^3} < \int_0^1\!\!dx\] \[\therefore \frac\pi4 <\int_0^1\!\!\frac{dx}{1+x^3} < 1\]

■

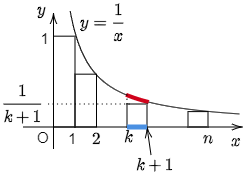
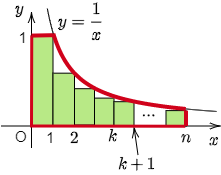
例題2　次を示せ． \[1+\frac12+\frac13+\cdots+\frac1n < 1+\log n\]

証明
　$\dfrac1x$ は $x\to0$ で発散するため，次の不等式では積分が計算できない： \[1+\dfrac12+\dfrac13+\cdots+\dfrac1n < \int_0^n\!\!\frac{dx}x\] 　正しくは最初の「1」を特別扱いにして，次のようにする： \[\begin{align*} 1+\dfrac12+\dfrac13+\cdots+\dfrac1n& < 1+\int_1^n\!\!\frac{dx}x\\ &=1+\Bigl[\log x\Bigr]_1^n\\ &=1+\log n \end{align*}\]

■

定理 \[ \int_a^b\!\!|f(x)|dx\geqq \left|\int_a^b\!\!f(x)dx\right| \]（等号成立は，閉区間 $[a,\ b]$ で $f(x)$ が定符号のとき）

例題　次を示せ． \[ \left|\int_{n\pi}^{(n+1)\pi}\!\!\frac{\sin x}{x^2}dx\right|< \frac 1\pi\left(\frac 1n-\frac 1{n+1}\right)\ \ (n=1,\ 2,\ \cdots) \]

証明 \[\begin{align*} \mbox{左辺}&\leqq\int_{n\pi}^{(n+1)\pi}\left|\frac{\sin x}{x^2}\right|dx\\ &<\int_{n\pi}^{(n+1)\pi}\!\!\frac{dx}{x^2}\\ &=\left[-\frac1x\right]_{n\pi}^{(n+1)\pi}\\ &=-\frac1{(n+1)\pi}+\frac1{n\pi}\\ &=\mbox{右辺} \end{align*}\]

■

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

---

高校数学[総目次]

数学Ⅲ　第3章　積分法

	スライド	ノート
1. 不定積分	[無料]
2. 置換積分法（不定積分）	[無料]
3. 部分積分法（不定積分）	[無料]
4. 定積分とその性質	[会員]
5. 置換積分法（定積分）	[会員]
6. 部分積分法（定積分）	[会員]
7. 定積分と微分法	[会員]
8. 定積分と和の極限	[会員]
9. 定積分と不等式	[会員]
10. 定積分の応用（面積）	[会員]
11. 定積分の応用（体積）	[会員]
12. 定積分の応用（回転体の体積）	[会員]
13. 曲線の長さ