このページにある内容は,こちらのスライド(会員向け)でわかり易く説明しています.
※PC環境なら全画面表示でより見やすく,よりわかりやすい!
高校数学[総目次]
数学Ⅲ 第3章 積分法
12.定積分の応用(回転体の体積)
12.1 回転体の体積
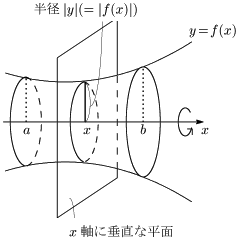
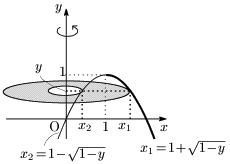
曲線 $y=f(x)$ と $x$ 軸,及び2直線 $x=a$,$x=b$ $(a < b)$ で囲まれた部分を $x$ 軸のまわりに1回転させてできる回転体の体積を $V$ とする.
この立体を $x$ 軸と垂直な平面で切ってできる切り口は,半径 $|y|\ (=|f(x)|)$ の円であるから,切り口の面積は,
\[\pi y^2\ (=\pi\{f(x)\}^2)\]
である.従って,次が成り立つ:
回転体の体積
\[V=\pi\int_a^b\!\!y^2\,dx=\pi\int_a^b\!\!\{f(x)\}^2\,dx\]
例題 半径 $r$ の球の体積 $V$ を求めよ.
こたえ
解答例を表示する
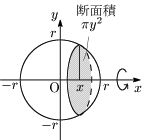
球の中心を原点とする.半径 $r$ の球は円 $x^2+y^2=r^2$ で囲まれた部分を $x$ 軸のまわりに回転させてできる回転体と考えることができるから,
\[\begin{align*}
V&=\pi\int_{-r}^r\!\!y^2\,dx\\[5pt]
&=\pi\int_{-r}^r\!\!(r^2-x^2)\,dx\\[5pt]
&=-\pi\int_{-r}^r\!\!(x+r)(x-r)\,dx\\[5pt]
&=\frac\pi6\{r-(-r)\}^3\\[5pt]
&=\underline{\boldsymbol{\frac43\pi r^3}}
\end{align*}\]
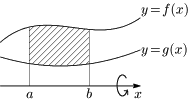
12.2 2曲線の間の領域の回転体
関数 $f(x),\ g(x)$ が区間 $[a,b]$ で常に $f(x)\geqq g(x)\geqq0$ であるとする.このとき,2曲線 $y=f(x),\ y=g(x)$,及び 2直線 $x=a,\ x=b$ で囲まれた部分を $x$ 軸のまわりに1回転して得られる回転体の体積 $V$ は
\[\begin{align*}
V&=\pi\int_a^b\!\!\{f(x)\}^2\,dx-\pi\int_a^b\!\!\{g(x)\}^2\,dx\\[5pt]
&=\pi\int_a^b\!\!(f^2-g^2)\,dx\\[5pt]
& (f,\,g\ \mbox{のあとの「} \,(x)\, \mbox{」を省略した.})
\end{align*}\]
2曲線で囲まれる回転体の体積
\[V=\pi\int_a^b\!\!(f^2-g^2)\,dx\]
注意
$V=\pi\displaystyle\int_a^b\!\!(f-g)^2\,dx$ ではない!!
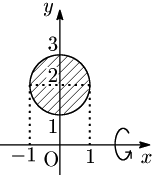
例題 円 $x^2+(y-2)^2=1$ の $x$ 軸まわりの回転体の体積 $V$ を求めよ.
こたえ
解答例を表示する
$x^2+(y-2)^2=1$ を $y$ について解くと,
\[y=\left\{\begin{array}{ll}
2+\sqrt{1-x^2}&(\mbox{円の上半分})\ \cdots\mbox{①}\\[5pt]
2-\sqrt{1-x^2}&(\mbox{円の下半分})\ \cdots\mbox{②}
\end{array}\right.\]
①$\geqq$②$\geqq 0$ であるから,
\[\begin{align*}
V&=\pi\int_{-1}^1\!\!\left(\mbox{①}^2-\mbox{②}^2\right)\,dx\\[5pt]
&=8\pi\int_{-1}^1\!\!\sqrt{1-x^2}\,dx\\[5pt]
&=8\pi\times\frac\pi2\\[5pt]
&=\underline{\boldsymbol{4\pi^2}}
\end{align*}\]
補足
$\displaystyle\int_{-1}^1\!\sqrt{1-x^2}\,dx=\frac\pi2$ の部分は積分を実行するのではなく,直ちに $\dfrac\pi2$ と答えたい.詳しくは こちら を参照.
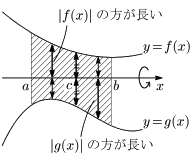
12.3 領域が回転軸をまたぐ場合
回転領域が回転軸をまたぐとき,短い方を回転して得られる部分は,長い方を回転して得られる部分にすっぽりと含まれる.
例えば,$a\leqq x\leqq b$ において,2曲線 $y=f(x)$ と $y=g(x)$,及び2直線 $x=a,\ x=b$ で囲まれる部分に $x$ 軸があり,区間 $[a,\ c]$ で $|f(x)|\geqq|g(x)|$ ,区間 $[c,b]$ で $|f(x)|\leqq|g(x)|$ であるとき,$x$ 軸のまわりに回転して得られる回転体の体積は,
\[\pi\int_a^c\!\!\{f(x)\}^2\,dx+\pi\int_c^b\!\!\{g(x)\}^2\,dx\]
となる.
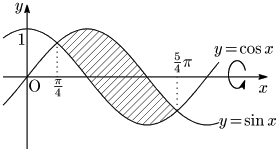
例題 $\dfrac\pi4\leqq x\leqq\dfrac54\pi$ で2曲線 $y=\sin x$ と $y=\cos x$ によって囲まれる部分を $x$ 軸のまわりに回転させてできる立体の体積 $V$ を求めよ.
こたえ
解答例を表示する
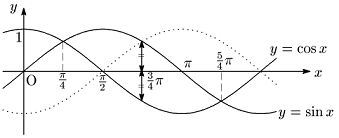
対称性により,$\dfrac\pi4\leqq x\leqq\dfrac34\pi$ の部分を考える.$\dfrac\pi2\leqq x\leqq\dfrac34\pi$ における $y=\cos x$ のグラフを $x$ 軸に関して折り返すと,$y=\sin x$ の下側になるので,
\[\begin{align*}
V&=2\times\pi\left(\int_{\frac\pi4}^{\frac34\pi}\!\sin^2 x\,dx-\int_{\frac\pi4}^{\frac\pi2}\!\cos^2 x\,dx\right)\\[5pt]
&=\cdots=\underline{\boldsymbol{\frac{\pi^2}4+\frac32\pi}}
\end{align*}\]
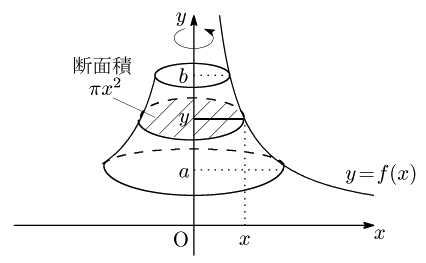
12.4 $y$ 軸まわりの回転体
図のような曲線 $y=f(x)$ と $y$ 軸,及び 2直線 $y=a,\ y=b$ とで囲まれる部分を $y$ 軸のまわりに1回転して得られる回転体の体積 $V$ は,$y$ 軸に垂直な平面で切った断面積が $\pi x^2$ であるから,次で与えられる:
${\boldsymbol y}$ 軸まわりの回転体の体積
\[V=\pi\int_a^b\!\!x^2\,dy\]
例題 曲線 $y=4-x^2$ と $x$ 軸,$y$ 軸とで囲まれた部分の $y$ 軸まわりの回転体の体積 $V$ を求めよ.
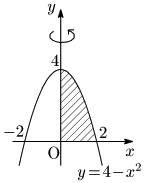
こたえ
解答例を表示する
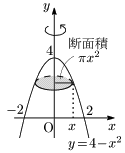
$y=4-x^2$ より $x^2=4-y$ であるから,
\[\begin{align*}
V&=\pi\int_0^4\!\!x^2\,dy\\[5pt]
&=\pi\int_0^4\!\!(4-y)\,dy\\[5pt]
&=\pi\left[-\frac{(4-y)^2}2\right]_0^4\\[5pt]
&=\underline{\boldsymbol{8\pi}}
\end{align*}\]
上の例では $x^2$ を $y$ の式で簡単に表すことができた.($y=4-x^2\to x^2=4-y$)
しかし,いつでもそのようなことが可能かといえば,そうとも限らない.
$y=f(x)$ から $x^2$ を $y$ の式で表しにくいときは(また表しにくくなくても),積分変数を $y$ から $x$ に変換(置換積分)して次のように計算できる:
${\boldsymbol y}$ 軸方向から ${\boldsymbol x}$ 軸方向の積分へ
\[\pi\int_a^b\!\!x^2\,dy=\pi\int_\alpha^\beta\!\!x^2\frac{dy}{dx}\,dx\]
ただし,$y$ が $a$ から
$b$ まで変化するとき,$x$ は $\alpha$ から $\beta$ まで変化する.
例題 曲線 $y=\cos x\ (0\leqq x\leqq\dfrac\pi2)$ と $x$ 軸,$y$ 軸で囲まれた部分の $y$ 軸まわりの回転体の体積 $V$ を求めよ.
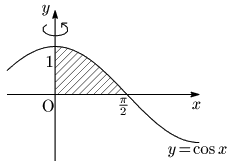
こたえ
解答例を表示する
$y=\cos x$ より
\[dy=-\sin x\,dx,\ \ \begin{array}{c|c}
y&0\to 1\\[5pt]\hline
x&\frac\pi2\to0
\end{array}\]
よって,
\[\begin{align*}
V&=\pi\int_0^1\!\!x^2\,dy\\[5pt]
&=\pi\int_{\frac\pi2}^0\!\!x^2\,\cdot(-\sin x)\,dx\\[5pt]
&=\pi\int_0^{\frac\pi2}\!\!x^2\sin x\,dx\\[5pt]
&=\cdots=\underline{\boldsymbol{\pi^2-2\pi}}
\end{align*}\]
12.5 単調ではない曲線の $y$ 軸まわりの回転体
$f(x)$ が単調でなければ,$y$ 軸まわりの回転体の体積の計算はややこしい.
例題 曲線 $y=-x^2+2x$ と $x$ 軸とで囲まれた部分の $y$ 軸まわりの回転体の体積 $V$ を求めよ.
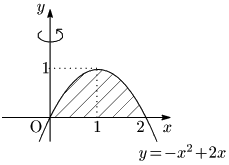
こたえ
解答例を表示する
補足
バウムクーヘン分割 という逃げ道もある.
12.6 一般の回転体
考え方はこれまでと同じで,
回転軸に垂直な平面での切り口を考える
例題 曲線 $y=x^2$ と直線 $y=x$ で囲まれた部分を,直線 $y=x$ のまわりに 1 回転して得られる立体の体積 $V$ を求めよ.
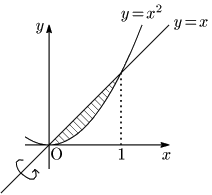
こたえ
解答例を表示する
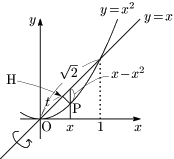
曲線 $y=x^2$ 上の点Pから直線 $y=x$ に下ろした垂線の足をH, OH$=t$ とおくと,
\[\begin{align*}
V&=\pi\int_0^{\sqrt2}\!\!{\rm PH}^2\,dt\\[5pt]
&=\pi\int_0^{\sqrt2}\!\!\{(x-x^2)\cos45^\circ\}^2\,dt\\[5pt]
&=\frac\pi2\int_0^{\sqrt2}(x-x^2)^2\,dt
\end{align*}\]
ここで,$x$ と $t$ の関係
\[t=\sqrt2x-\frac{x-x^2}{\sqrt2}=\frac{x+x^2}{\sqrt2}\]
により,
\[dt=\frac{1+2x}{\sqrt2}\,dx,\ \ \begin{array}{c|c}
t&0\to \sqrt2\\\hline
x&0\to1
\end{array}\]
よって,
\[\begin{align*}
V&=\frac\pi2\int_0^1\!\!(x-x^2)^2\cdot\frac{1+2x}{\sqrt2}\,dx\\[5pt]
&=\cdots=\underline{\boldsymbol{\frac{\sqrt2}{60}\pi}}
\end{align*}\]
12.7 媒介変数表示と体積
ポイント
媒介変数表示を生かして媒介変数で積分する.
例題 サイクロイド $\left\{\begin{array}{l}x=a(t-\sin t)\\ y=a(1-\cos t)\end{array}\right.\ (a>0,\ 0\leqq t\leqq 2\pi)$ と $x$ 軸で囲まれた部分について,$x$ 軸まわりの回転体の体積 $V$ を求めよ.
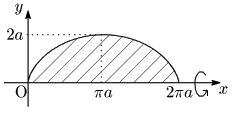
こたえ
解答例を表示する
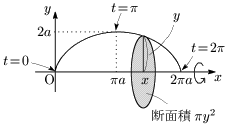
$x=a(t-\sin t)$ より,
\[dx=a(1-\cos t)\,dt,\ \ \begin{array}{c|c}
x&0\to 2\pi a\\\hline
t&0\to 2\pi
\end{array}\]
であるから,
\[\begin{align*}
V&=\pi\int_0^{2\pi a}\!\!y^2\,dx\\[5pt]
&=\pi\int_0^{2\pi}\{a(1-\cos t)\}^2\cdot a(1-\cos t)\,dt\\[5pt]
&=\pi a^3\int_0^{2\pi}(1-\cos t)^3\,dt\\[5pt]
&=\pi a^3\int_0^{2\pi}(1-3\cos t+3\cos^2t-\cos^3t)\,dt\\[5pt]
&=\cdots=\underline{\boldsymbol{5\pi^2a^3}}
\end{align*}\]
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第3章 積分法