10. 定積分の応用(面積)(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅲ　第3章　積分法

	スライド	ノート
1. 不定積分	[無料]
2. 置換積分法（不定積分）	[無料]
3. 部分積分法（不定積分）	[無料]
4. 定積分とその性質	[会員]
5. 置換積分法（定積分）	[会員]
6. 部分積分法（定積分）	[会員]
7. 定積分と微分法	[会員]
8. 定積分と和の極限	[会員]
9. 定積分と不等式	[会員]
10. 定積分の応用（面積）	[会員]
11. 定積分の応用（体積）	[会員]
12. 定積分の応用（回転体の体積）	[会員]
13. 曲線の長さ

10．定積分の応用(面積)

10.1 面積

閉区間 $[a,\ b]$ で連続な関数 $f(x)$ と， $x$ 軸，及び2直線 $x=a,\ x=b$ とで囲まれる部分の面積は \[\int_a^b\!\!|f(x)|dx\]

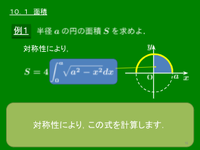
例題1 　半径 $a$ の円の面積 $S$ を求めよ．

答

　解答例を表示する >

　$x^2+y^2=a^2$ を $y$ について解くと， \[y=\left\{\begin{array}{ll} \sqrt{a^2-x^2}&(\mbox{円の上半分})\\[5pt] -\sqrt{a^2-x^2}&(\mbox{円の下半分}) \end{array}\right.\] 　従って対称性により， \[S=4\int_0^a\!\!\sqrt{a^2-x^2}\,dx\] 　$x=a\cos\theta$ とおくと， \[dx=-a\sin\theta\,d\theta,\ \ \begin{array}{c|c} x&0\to 1\\\hline \theta&\frac\pi2\to 0 \end{array},\] \[\sqrt{a^2-x^2}=\sqrt{a^2(1-\cos^2\theta)}=|a\sin\theta|=a\sin\theta\] \[(\because a>0.\ \ \mbox{また，}0\leqq\theta\leqq\frac\pi2\mbox{で}\sin\theta\geqq0)\] \[\begin{align*} \therefore S&=4\int_{\frac\pi2}^0a\sin\theta\cdot(-a\sin\theta)\,d\theta\\[5pt] &=4a^2\int_0^{\frac\pi2}\sin^2\theta\,d\theta\\[5pt] &=4a^2\int_0^{\frac\pi2}\frac{1-\cos2\theta}2\,d\theta\\[5pt] &=2a^2\left[\theta-\frac12\sin2\theta\right]_0^{\frac\pi2}\\[5pt] &=\underline{\pi a^2} \end{align*}\]

補足

　$\displaystyle\int_\alpha^\beta\!\!\sqrt{a^2-x^2\ }\,dx$ 型の積分の計算では，置換積分を行うのではなく，円の面積に帰着させるのが実践的：

　$a>0$ のとき， \[\begin{align*} &\int_0^a\!\!\sqrt{a^2-x^2}\,dx=\frac{\pi a^2}4\ \ (\mbox{円の}1/4\mbox{の面積})\\[5pt] &\int_{-a}^a\!\!\sqrt{a^2-x^2}\,dx=\frac{\pi a^2}2\ \ (\mbox{半円の面積})\\[5pt] &\int_{-\frac a2}^a\!\!\sqrt{a^2-x^2}\,dx=\frac{\sqrt3 a^2}8+\frac{\pi a^2}3\\ \end{align*}\]

(3番目の式は，右辺第1項が直角三角形の面積，第2項が中心角 120$^\circ$ の扇形の面積)

例題2 　楕円 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\ (a>0,b>0)$ の面積 $S$ を求めよ．

答

　解答例を表示する >

　楕円の式を $y$ について解くと， \[y=\left\{\begin{array}{ll} \ \ \dfrac ba\sqrt{a^2-x^2}&(\mbox{楕円の上半分})\\ -\dfrac ba\sqrt{a^2-x^2}&(\mbox{楕円の下半分}) \end{array}\right.\] 　対称性により，$x\geqq0,\ y\geqq0$ の部分の4倍が求めるものであるから， \[\begin{align*} S&=4\int_0^a\!\!\frac ba\sqrt{a^2-x^2}\,dx\\ &=\frac{4b}a\underline{\int_0^a\!\!\sqrt{a^2-x^2}\,dx}_{\mbox{①}} \end{align*}\] 　下線①の積分は半径 $a$ の円の4分の1の面積に等しいから， \[S=\frac{4b}a\cdot\frac{\pi a^2}4=\underline{\pi ab}\]

補足

　$S=\pi ab$ は半径 $a$ の円の面積の $\dfrac ba$ 倍となっているが， \[y=\frac ba\sqrt{a^2-x^2}\] という式を見れば，各 $x$ に対して $y$ の値が，常に円の場合 $(\sqrt{a^2-x^2}\,)$ の $\dfrac ba$ 倍となっているところからも納得できる．

10.2 2曲線に囲まれた部分の面積

　2曲線 $y=f(x)$と$y=g(x)$，及び2直線 $x=a,\ x=b$ （ただし，$a<b$）で囲まれる部分の面積は \[ \int_a^b\!\!|f(x)-g(x)|dx \]

例題 　曲線 $y=x^2\,(-2\leqq x\leqq 1)$ と3直線 $y=x+2,\ x=-2,\ x=1$ で囲まれる部分の面積 $S$ を求めよ．

答

　解答例を表示する >

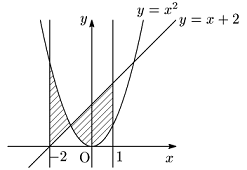
　$x^2=x+2$ より $x^2-x-2=0$．
　$(x+1)(x-2)=0$　$\therefore x=-1, 2$． \[\begin{align*} S&=\int_{-2}^1\!\!|x^2-(x+2)|\,dx\\[5pt] &=\int_{-2}^{-1}\!\{x^2-(x+2)\}\,dx-\int_{-1}^1\!\!\{x^2-(x+2)\}\,dx \end{align*}\] 　ここで，$F(x)=\dfrac13x^3-\dfrac12x^2-2x$ とおくと， \[\begin{align*} S&=\Bigl[F(x)\Bigr]_{-2}^{-1}-\Bigl[F(x)\Bigr]_{-1}^1\\[5pt] &=2F(-1)-F(-2)-F(1)\\[5pt] &=\cdots=\underline{\frac{31}6} \end{align*}\]

10.3 媒介変数(パラメータ)表示と面積

ポイント 　媒介変数(パラメータ)を消去せず，そのままの形を生かす： \[\int\!\!y\,dx=\int\!\!y\frac{dx}{dt}\,dt\ \ (\mbox{置換積分})\]

例題1 　半径1の円の面積 $S$ を求めよ．

答

　解答例を表示する >

　円周上の点の座標 $(x,y)$ は，パラメータ $\theta$ を用いて \[\left\{\begin{array}{l} x=\cos\theta\\ y=\sin\theta \end{array}\right.\] と表されるから，対称性を考慮すると， \[S=4\int_0^1\!\!y\,dx=4\int_0^1\!\!\sin\theta\,dx\] (誤1)　　$\displaystyle S=\Bigl[-\cos\theta\Bigr]_0^1$　(??)
　　　　($x$ ではなく，$\theta$ で積分してしまっている)
(誤2)　　$\displaystyle S=4\sin\theta\int_0^1\!\!dx$　(??)
　　　　($x=\cos\theta$ だから，$\sin\theta$ は定数ではない)
(正) 　$\ x=\cos\theta$より， \[dx=-\sin\theta\,d\theta,\ \ \begin{array}{c|c} x&0\to 1\\\hline \theta&\frac\pi2\to 0 \end{array}\] 　　であるから， \[\begin{align*} S&=4\int_{\frac\pi2}^0\!\!\sin\theta\cdot(-\sin\theta)\,d\theta\\[5pt] &=4\int_0^{\frac\pi2}\!\!\sin^2\theta\,d\theta\\[5pt] &=4\int_0^{\frac\pi2}\!\!\frac{1-\cos2\theta}2 d\theta\\[5pt] &=2\Bigl[\theta-\frac12\sin2\theta\Bigr]_0^{\frac\pi2}\\[5pt] &=\underline{\pi} \end{align*}\]

例題2 　曲線 $\left\{\begin{array}{l}x=2\sqrt2\cos\theta\\ y=\dfrac 12\sin 2\theta\end{array}\right. \ (0\leqq \theta\leqq \dfrac \pi 2)$ と $x$ 軸とで囲まれた部分の面積$S$を求めよ．

答

　解答例を表示する >

\[\begin{align*} &\frac{dx}{dt}=-2\sqrt2\sin\theta\ \ (\leqq0)\\[5pt] &\frac{dy}{dt}=\cos2\theta \end{align*}\] 　よって，$\theta$ が０から $\dfrac\pi2$ まで変化したときの $x,y$ の変化は次のようになる：



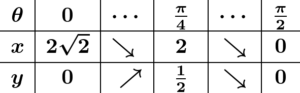
　従って曲線の概形は次のようになる：



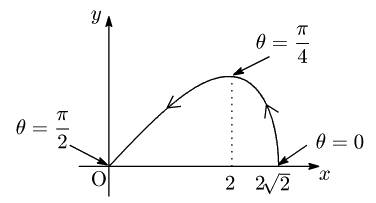
　従って， \[\begin{align*} S&=\int_0^{2\sqrt2}\!\!y\,dx\\[5pt] &=\int_{\frac\pi2}^0\!\frac12\sin2\theta\cdot(-2\sqrt2\sin\theta)\,d\theta\\[5pt] &=\sqrt2\int_0^{\frac\pi2}\sin2\theta\sin\theta\,d\theta\\[5pt] &=\cdots=\underline{\frac{2\sqrt2}3} \end{align*}\]

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]

数学Ⅲ　第3章　積分法

	スライド	ノート
1. 不定積分	[無料]
2. 置換積分法（不定積分）	[無料]
3. 部分積分法（不定積分）	[無料]
4. 定積分とその性質	[会員]
5. 置換積分法（定積分）	[会員]
6. 部分積分法（定積分）	[会員]
7. 定積分と微分法	[会員]
8. 定積分と和の極限	[会員]
9. 定積分と不等式	[会員]
10. 定積分の応用（面積）	[会員]
11. 定積分の応用（体積）	[会員]
12. 定積分の応用（回転体の体積）	[会員]
13. 曲線の長さ