高校数学[総目次]
高校数学ワンポイント
| スライド | ノート | |
| 1. ファクシミリの原理 | [会員] | |
| 2. バウムクーヘン分割 | [会員] | |
| 3. 円と放物線 | ||
| 4. 垂線の長さ | ||
| 5. 不定方程式 | ||
| 6. 関数の連続性は導関数に遺伝するか | ||
| 7. 極方程式における $r$ の正負について | ||
| 8. 極座標表示における扇形分割積分 | ||
| 9. 素因数分解の一意性 | ||
| 10. 三角関数の不定積分 | ||
| 11. コーシー・シュワルツの不等式 | ||
| 12. 放物線と2接線で囲まれた部分の面積 | ||
| 13. 整式の除法(発展編) | ||
| 14. 3次関数のグラフの特徴 | ||
| 15. 曲線の長さを求める公式の証明について | ||
| 16. もう迷わない!必要条件・十分条件のくすっと笑える判定方法 |
1.よくある誤答
まずは次の問題と解答と怪答(??)の3つを見てください.
問題 関数 $f(x)=|x|$ は $x=0$ で微分可能ではないことを示せ.
解答
$x > 0$ のとき,$f(x)=x$ であるから
\[\lim_{h\to +0}\frac{f(0+h)-f(0)}h=\lim_{h\to +0}\frac {h-0}h=1\]
また,$x < 0$ のとき,$f(x)=-x$ であるから,
\[\lim_{h\to -0}\frac{f(0+h)-f(0)}h=\lim_{h\to -0}\frac{-h-0}h=-1\]
従って右側極限と左側極限が一致しないから $\displaystyle\lim_{h\to0}\frac{f(0+h)-f(0)}h$ は存在しない.
故に,$f(x)$ は $x=0$ で微分可能ではない.
さて,次の怪答(??)は正しいでしょうか?
怪答(??)
$x > 0$ のとき,$f(x)=x.$
よって $f'(x)=1$ であるから $\displaystyle\lim_{x\to +0}f'(x)=1.$
また,$x < 0$ のとき,$f(x)=-x.$
よって $f'(x)=-1$ であるから $\displaystyle\lim_{x\to -0}f'(x)=-1.$
従って$\displaystyle{\lim_{x\to +0}f'(x)\neq \lim_{x\to -0}f'(x)}$ であるから $f'(0)$ は存在しない.
故に,$f(x)$ は $x=0$ で微分可能ではない.
(??)
上の「怪答(??)」は,
$\displaystyle\lim_{x\to 0}f'(x)$ が存在しない $\Longrightarrow$ $f'(0)$ が存在しない
というもので,つまりは $f'(x)$ の $x=0$ での連続性 \[ \lim_{x\to 0}f'(x)=f'(0) \] を論拠としているように見えますが,これは正しいでしょうか?確かに元の関数 $f(x)=|x|$ は連続関数です.果たして連続関数ならば常にその導関数も連続関数なのでしょうか?
結論から言いますと,$f(x)$ がある区間で連続であっても,導関数 $f'(x)$ の方は必ずしも連続とは限りません.つまり
連続性は導関数には遺伝しない
のです.そのことを次の例で確認してみましょう.2.連続性が遺伝しない例
上の問題では関数 $y=|x|$ が実際に $x=0$ で微分可能ではないため,怪答(??) の論理ミスに気が付きにくくなってしまっています.次の関数の例を見れば,怪答(??) がどうしていけないのかはっきりわかることでしょう.
例
\[f(x)=\left\{ \begin{array}{ll} x^2\cos\dfrac 1x&(x\neq 0)\\ 0&(x=0) \end{array} \right. \]
まず関数 $f(x)$ が連続関数であることを確認しておきます.
$x\neq0$ ならばもちろん任意の実数 $x$ で連続です.$x=0$ での連続性は,$-1\leqq \cos\dfrac1x\leqq1$ により
\[-x^2\leqq x^2\cos\frac1x\leqq x^2\]
と評価できますから,はさみうちの原理により,
\[\lim_{x\to0}x^2\cos\frac1x=0.\]
従って,
\[\lim_{x\to0}f(x)=f(0)\]
が成り立ちますから,$f(x)$ は $x=0$ でも連続です.
以上により,$f(x)$が実数全体で連続であることがわかりました.
次に,導関数 $f\,'(x)$ についてみてみましょう.
$x\neq 0$ では
\[\begin{align*}
f\,'(x)&=2x\cos\frac 1x-x^2\sin\frac 1x\cdot\left(-\frac 1{x^2}\right)\\[5pt]
&=2x\cos\frac 1x+\sin\frac 1x\\[5pt]
\end{align*}\]
となります.$x=0$ のときは,上の式は使えませんから微分係数の定義にあてはめて
\[\begin{gather*}
\left|\frac{f(h)-f(0)}h\right|=\left|\frac{h^2\cos(1/h)-0}h\right|=\left|h\cos\frac 1h\right|\leqq |h|.\\[5pt]
\therefore\ \lim_{h\to 0}\frac{f(h)-f(0)}h=0.
\end{gather*}\]
即ち,$x=0$ でも微分可能で $f\,'(0)=0$ となりますから,$f\,'(x)$ はまとめると次のようになります:
\[f\,'(x)=\left\{ \begin{array}{ll} 2x\cos\dfrac 1x+\sin\dfrac 1x&(x\neq 0)\ \ \ \cdots \mbox{①}\\ 0&(x=0) \end{array} \right.\]
それでは $f\,'(x)$ の連続性についてはどうでしょうか.$x\neq 0$ においては①式により $f\,'(x)$ は連続ですが,$x=0$ では \[ \lim_{x\to 0}f\,'(x)=f\,'(0) \] となっているかどうかを確かめてみる必要があります.①式において $x\to 0$ のとき,$x\cos\dfrac1x$ の部分ははさみうちの原理により 0 に収束しますが,$\sin\dfrac 1x$ の部分が収束しませんから,結局 $\displaystyle{\lim_{x\to 0}f\,'(x)}$ は存在しません.ところが先に計算したように,$f\,'(0)$ の値は0であり,ちゃんと存在しています.即ち
$\displaystyle\lim_{x\to 0}f\,'(x)$ が存在しない $\Longrightarrow$ $f\,'(0)$ が存在しない
は正しくないのです.
以上により,$f(x)$ は連続関数であるけれども,その導関数である $f'(x)$ は連続関数ではないことがわかりました.つまり関数の連続性は,導関数に遺伝するとは限らないのです.
ちなみに $y=f(x)$ のグラフの概形は次のようになります.
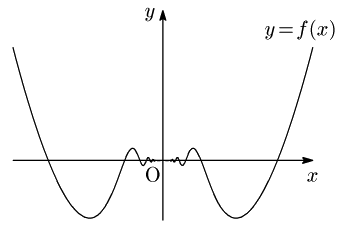
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
高校数学ワンポイント
| スライド | ノート | |
| 1. ファクシミリの原理 | [会員] | |
| 2. バウムクーヘン分割 | [会員] | |
| 3. 円と放物線 | ||
| 4. 垂線の長さ | ||
| 5. 不定方程式 | ||
| 6. 関数の連続性は導関数に遺伝するか | ||
| 7. 極方程式における $r$ の正負について | ||
| 8. 極座標表示における扇形分割積分 | ||
| 9. 素因数分解の一意性 | ||
| 10. 三角関数の不定積分 | ||
| 11. コーシー・シュワルツの不等式 | ||
| 12. 放物線と2接線で囲まれた部分の面積 | ||
| 13. 整式の除法(発展編) | ||
| 14. 3次関数のグラフの特徴 | ||
| 15. 曲線の長さを求める公式の証明について | ||
| 16. もう迷わない!必要条件・十分条件のくすっと笑える判定方法 |
