4. ベクトルの内積(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学B　第1章　ベクトル

	スライド	ノート
1. ベクトルと有向線分	[無料]
2. ベクトルの演算	[無料]
3. ベクトルの成分	[無料]
4. ベクトルの内積	[会員]
5. 位置ベクトル	[会員]
6. ベクトル方程式	[会員]
7. 平面ベクトルの応用	[会員]
8. 空間ベクトル	[会員]
9. 空間ベクトルの成分	[会員]
10. 空間ベクトルの内積	[会員]
11. 空間の位置ベクトル	[会員]
12. 空間ベクトルの応用	[会員]
13. 空間のベクトル方程式	[会員]

4.　ベクトルの内積

4.1　内積

ベクトルのなす角

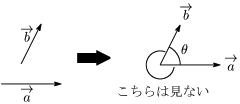
　2つのベクトル $\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ について，2つの始点が一致するように平行移動させたときにできる角(図の$\theta$，ただし $0\leqq\theta\leqq\pi$)を，$\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ のなす角という．

内積

　$\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ のなす角を $\theta$ とするとき， \[|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut b}|\cos\theta\] を $\boldsymbol{\overrightarrow{\mathstrut a}}$ と $\boldsymbol{\overrightarrow{\mathstrut b}}$ の内積といい， \[\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}\] で表す：

ベクトルの内積 　$\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ のなす角を $\theta$ とするとき， \[\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}=|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut b}|\cos\theta\]

　$\overrightarrow{\mathstrut a}=\overrightarrow{\mathstrut 0}$ または $\overrightarrow{\mathstrut b}=\overrightarrow{\mathstrut 0}$ のときは，$\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}=0$ と定める．

　$\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut a}=|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut a}|\cos 0^\circ=|\overrightarrow{\mathstrut a}|^2$ であるから，

\[|\overrightarrow{\mathstrut a}|^2=\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut a}\ \ \ \left(|\overrightarrow{\mathstrut a}|=\sqrt{\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut a}}\ \right)\]

4.2　内積と成分

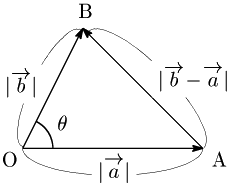
　△OABにおいて，$\overrightarrow{\mathstrut\rm OA}=\overrightarrow{\mathstrut a}=(a_1,a_2)$，$\overrightarrow{\mathstrut\rm OB}=\overrightarrow{\mathstrut b}=(b_1,b_2)$ とし，$\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ のなす角を $\theta$ とする．
　余弦定理により， \[{\rm AB}^2={\rm OA}^2+{\rm OB}^2-2{\rm OA}\cdot{\rm OB}\cos\theta\] 　この式は，$\theta=0^\circ$ や $180^\circ$ のときも成り立つ．ベクトルで表せば， \[|\overrightarrow{\mathstrut b}-\overrightarrow{\mathstrut a}|^2=|\overrightarrow{\mathstrut a}|^2+|\overrightarrow{\mathstrut b}|^2-2\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}\] \[\begin{align*} \therefore \overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}&=\frac{|\overrightarrow{\mathstrut a}|^2+|\overrightarrow{\mathstrut b}|^2-|\overrightarrow{\mathstrut b}-\overrightarrow{\mathstrut a}|^2}2\\[5pt] &=\frac{({a_1}^2\!+\!{a_2}^2)\!+\!({b_1}^2\!+\!{b_2}^2)\!-\!\{(b_1\!-\!a_1)^2\!+\!(b_2\!-\!a_2)^2\}}2\\[5pt] &=\frac{2(a_1\,b_1+a_2\,b_2)}2\\[5pt] &=a_1\,b_1+a_2\,b_2 \end{align*}\] 　これは，$\overrightarrow{\mathstrut a}=\overrightarrow{\mathstrut 0}$，または $\overrightarrow{\mathstrut b}=\overrightarrow{\mathstrut 0}$ のとき，即ち $(a_1,a_2)=(0,0)$，または $(b_1,b_2)=(0,0)$ のときも成立．

内積と成分　$\overrightarrow{\mathstrut a}=(a_1,\ a_2)$，$\overrightarrow{\mathstrut b}=(b_1,\ b_2)$ のとき， \[\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}=a_1\,b_1+a_2\,b_2\]

4.3　ベクトルのなす角

　$\overrightarrow{\mathstrut 0}$ でない2つのベクトル $\overrightarrow{\mathstrut a}=(a_1,a_2)$，$\overrightarrow{\mathstrut b}=(b_1,b_2)$ のなす角を $\theta$ とすると， \[\overrightarrow{\mathstrut a}\cdot \overrightarrow{\mathstrut b}=|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut b}|\cos\theta\] \[\begin{align*} \therefore\ \cos\theta&=\frac{\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}}{|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut b}|}\\[5pt] &=\frac{a_1b_1+a_2b_2}{\sqrt{{a_1}^2+{a_2}^2}\sqrt{{b_1}^2+{b_2}^2}} \end{align*}\]

ベクトルのなす角と内積 $\overrightarrow{\mathstrut 0}$ でない2つのベクトル $\overrightarrow{\mathstrut a}=(a_1,a_2)$，$\overrightarrow{\mathstrut b}=(b_1,b_2)$ のなす角を $\theta$ とすると， \[\begin{align*} \therefore\ \cos\theta&=\frac{\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}}{|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut b}|}\\[5pt] &=\frac{a_1b_1+a_2b_2}{\sqrt{{a_1}^2+{a_2}^2}\sqrt{{b_1}^2+{b_2}^2}} \end{align*}\]

例題　$\overrightarrow{a}=(-1,\ -2),\ \overrightarrow{b}=(3,\ 1)$ のなす角 $\theta$ を求めよ．

こたえ

\[\begin{align*} \overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}&=-1\cdot3+(-2)\cdot1=-5\\[5pt] |\overrightarrow{\mathstrut a}|&=\sqrt{(-1)^2+(-2)^2}=\sqrt5\\[5pt] |\overrightarrow{\mathstrut b}|&=\sqrt{3^1+1^2}=\sqrt{10} \end{align*}\] 　よって， \[\cos\theta=\dfrac{-5}{\sqrt5\,\sqrt{10}}=-\dfrac1{\sqrt2}\] 　$0^\circ\leqq\theta\leqq180^\circ$ より，$\underline{\boldsymbol{\theta=135^\circ}}$

ベクトルの垂直

　$\overrightarrow{\mathstrut{a}}$ と $\overrightarrow{\mathstrut{b}}$ のなす角が $90^\circ$ のとき，「$\overrightarrow{\mathstrut{a}}$ と $\overrightarrow{\mathstrut{b}}$ は垂直である」といい， \[\overrightarrow{\mathstrut{a}}\perp \overrightarrow{\mathstrut{b}}\] で表す．

　$\overrightarrow{\mathstrut{a}}\perp \overrightarrow{\mathstrut{b}}$ のとき，$\cos90^\circ=0$ であるから， \[\overrightarrow{\mathstrut{a}}\cdot \overrightarrow{\mathstrut{b}}=|\overrightarrow{\mathstrut{a}}|\,|\overrightarrow{\mathstrut{b}}|\cos90^\circ=0\]

　逆に$\overrightarrow{\mathstrut{a}}\cdot \overrightarrow{\mathstrut{b}}=0$ のとき，2つのベクトルのなす角を $\theta$ とすると， \[|\overrightarrow{\mathstrut{a}}|\,|\overrightarrow{\mathstrut{b}}|\cos\theta=0\] 　よって，$|\overrightarrow{\mathstrut{a}}|\neq0$，かつ $|\overrightarrow{\mathstrut{b}}|\neq0$ ならば，$\cos\theta=0$．
　$0^\circ\leqq\theta\leqq180^\circ$ より，$\theta=90^\circ$．従って $\overrightarrow{\mathstrut{a}}\perp\overrightarrow{\mathstrut{b}}$．

　以上により次が成り立つ：

ベクトルの垂直条件　$\overrightarrow{\mathstrut{a}}\neq\overrightarrow{0}$ かつ$\overrightarrow{\mathstrut{b}}\neq\overrightarrow{0}$ のとき， \[\overrightarrow{\mathstrut{a}}\perp\overrightarrow{\mathstrut{b}}\iff\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{\mathstrut{b}}=0 \] 　$\overrightarrow{\mathstrut{a}}=(a_1,a_2)$，$\overrightarrow{\mathstrut{b}}=(b_1,b_2)$ と成分で表されているときは， \[\overrightarrow{a}\perp\overrightarrow{b}\iff a_1a_2+b_1b_2=0 \]

注意

「$\overrightarrow{\mathstrut{a}}\neq0$ かつ $\overrightarrow{\mathstrut{b}}\neq0$ 」の仮定がなければ，

\[\begin{align*} &\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{\mathstrut{b}}=0\\[5pt] \iff&\overrightarrow{\mathstrut{a}}\perp\overrightarrow{\mathstrut{b}}\ \underline{\boldsymbol{{\rm or}\ \overrightarrow{\mathstrut{a}}=\overrightarrow{\mathstrut{0}}\ {\rm or}\ \overrightarrow{\mathstrut{b}}=\overrightarrow{\mathstrut{0}}\ \ }} \end{align*}\]

のように下線部の条件が追加される．

4.4　内積の性質

内積の性質\begin{align*} &[1]\ \ \overrightarrow{\mathstrut{a}}\cdot\overrightarrow{b}=\overrightarrow{b}\cdot\overrightarrow{\mathstrut{a}}\ \ (\mbox{交換法則})\\[5pt] &[2]\ \ \overrightarrow{a}\cdot\overrightarrow{a}=\left|\overrightarrow{a}\right|^2\\[5pt] &[3]\ \ \overrightarrow{\mathstrut{a}}\cdot(\overrightarrow{b}+\overrightarrow{\mathstrut{c}})=\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{b}+\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{\mathstrut{c}}\ \ (\mbox{分配法則})\\[5pt] &[4]\ \ (\overrightarrow{\mathstrut{a}}+\overrightarrow{b})\cdot\overrightarrow{\mathstrut{c}}=\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{\mathstrut{c}}+\overrightarrow{b}\cdot\overrightarrow{\mathstrut{c}}\ \ (\mbox{分配法則})\\[5pt] &[5]\ \ (k\overrightarrow{\mathstrut{a}})\cdot\overrightarrow{b}=\overrightarrow{a}\cdot(k\overrightarrow{b})=k(\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{b})\ \ (k\mbox{ は実数}) \end{align*}

証明

　2つのベクトルのなす角を $\theta$ とする．

[1] \[\begin{align*} (\mbox{左辺}) &=|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut b}|\cos\theta\\[5pt] &=|\overrightarrow{\mathstrut b}||\overrightarrow{\mathstrut a}|\cos\theta\\[5pt] &=(\mbox{右辺}) \end{align*}\]

[2] \[\begin{align*} (\mbox{左辺}) &=|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut a}|\cos0^\circ\\[5pt] &=|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut a}|\\[5pt] &=(\mbox{右辺}) \end{align*}\]

[3]　$\overrightarrow{\mathstrut a}\!=\!(a_1,a_2)$,$\overrightarrow{\mathstrut b}\!=\!(b_1,b_2)$,$\overrightarrow{\mathstrut c}\!=\!(c_1,c_2)$ とすると， \[\begin{align*} (\mbox{左辺}) &=(a_1,a_2)\cdot(b_1+c_1,b_2+c_2)\\[5pt] &=a_1(b_1+c_1)+a_2(b_2+c_2)\\[5pt] &=(a_1b_1+a_2b_2)+(a_1c_1+a_2c_2)\\[5pt] &=(\mbox{右辺}) \end{align*}\]

[4]は，[3]と同様に示される．
　([1]と[3]を用いて示してもよい．)

[5]　$\overrightarrow{\mathstrut a}\!=\!(a_1,a_2)$,$\overrightarrow{\mathstrut b}\!=\!(b_1,b_2)$ とすると， \[\begin{align*} (\mbox{左辺})&=(ka_1,ka_2)\cdot(b_1,b_2)\\[5pt] &=ka_1b_1+ka_2b_2\\[5pt] &=\left\{ \begin{array}{l} a_1\!\times\! kb_1\!+\!a_2\!\times\! kb_2\!=\!(a_1,b_1)\cdot(kb_1,kb_2)\!=\!(\mbox{中辺})\\[5pt] k(a_1b_1+a_2b_2)=(\mbox{右辺}) \end{array}\right. \end{align*}\]

■

補足

　[5]により，$k(\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b})$ は簡単に $k\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}$ と書く．

注意

　$(\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b})\overrightarrow{\mathstrut c}=\overrightarrow{\mathstrut a}(\overrightarrow{\mathstrut b}\cdot\overrightarrow{\mathstrut c})$ のような式は成り立たない．

4.5　内積と正射影

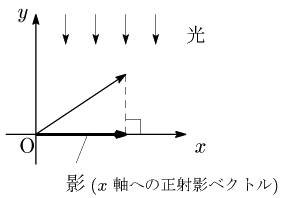
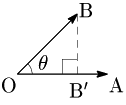
　2つのベクトル $\overrightarrow{\mathstrut\rm OA}$，$\overrightarrow{\mathstrut\rm OB}$ のなす角 $\theta$ が鋭角のとき，Bから直線OAに下ろした垂線の足を$\rm B’$とする．このとき $\overrightarrow{\mathstrut\rm OB’}$ を

$\overrightarrow{\mathstrut\rm OB}$ の $\overrightarrow{\mathstrut\rm OA}$(の上)への正射影ベクトル

という．

　$\cos\theta=\dfrac{\rm OB’}{\rm OB}$ より， \[\begin{align*} \overrightarrow{\mathstrut\rm OA}\cdot\overrightarrow{\mathstrut\rm OB}&=|\overrightarrow{\mathstrut\rm OA}||\overrightarrow{\mathstrut\rm OB}|\cos\theta\\[5pt] &={\rm OA}\cdot{\rm OB}\cdot\frac{\rm OB’}{\rm OB}\\[5pt] &={\rm OA}\cdot{\rm OB’} \end{align*}\] 　このことから，内積の図形的な意味は次のようになる：

内積の図形的な意味　$\overrightarrow{\mathstrut 0}$ でない2つのベクトル $\overrightarrow{\mathstrut\rm OA}$，$\overrightarrow{\mathstrut\rm OB}$ のなす角が鋭角のとき，それらの内積は，$\overrightarrow{\mathstrut\rm OA}$ の大きさと，$\overrightarrow{\mathstrut\rm OB}$ の $\overrightarrow{\mathstrut\rm OA}$ への正射影ベクトルの大きさとの積である．

重要例題
　$\overrightarrow{\mathstrut 0}$ でない2つのベクトル $\overrightarrow{\mathstrut a}$，$\overrightarrow{\mathstrut b}$ について，$\overrightarrow{\mathstrut b}$ の $\overrightarrow{\mathstrut a}$ への正射影ベクトル $\overrightarrow{\mathstrut c}$ を，$\overrightarrow{\mathstrut a}$，$\overrightarrow{\mathstrut b}$ を用いて表せ．

答

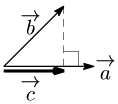
　$\overrightarrow{\mathstrut c}=k\,\overrightarrow{\mathstrut a}$ ($k$ は実数)とおける．
　$\overrightarrow{\mathstrut a}\perp(\overrightarrow{\mathstrut c}-\overrightarrow{\mathstrut b})$ より，$\overrightarrow{\mathstrut a}\cdot(\overrightarrow{\mathstrut c}-\overrightarrow{\mathstrut b})=0$．
　　　$\therefore \overrightarrow{\mathstrut a}\cdot(k\,\overrightarrow{\mathstrut a}-\overrightarrow{\mathstrut b})=0$
　　　　$\therefore k=\dfrac{\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}}{|\overrightarrow{\mathstrut a}|^2}$

　故に，$\underline{\boldsymbol{\overrightarrow{\mathstrut c}=\dfrac{\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}}{|\overrightarrow{\mathstrut a}|^2}\overrightarrow{\mathstrut a}}}$

正射影ベクトル　$\overrightarrow{\mathstrut 0}$ でない2つのベクトル $\overrightarrow{\mathstrut a}$，$\overrightarrow{\mathstrut b}$ について，$\overrightarrow{\mathstrut b}$ の $\overrightarrow{\mathstrut a}$ への正射影ベクトルは， \[\frac{\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}}{|\overrightarrow{\mathstrut a}|^2}\overrightarrow{\mathstrut a}\]

よくある質問

正射影される側のベクトル(例えば $\boldsymbol{\overrightarrow{\mathstrut a}}$ )の大きさや向きが変わると，正射影ベクトルはどうなりますか？

正射影される側のベクトル $\overrightarrow{\mathstrut a}$ の「大きさ」が変わっても正射影ベクトルは変化しない．また $\overrightarrow{\mathstrut a}$ に射影する場合も $-\overrightarrow{\mathstrut a}$ (「向き」が逆のベクトル)に射影する場合も正射影ベクトルは同じになる．

※　以上の質問に対する詳しい解説はスライド (会員)で．

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

---

高校数学[総目次]

数学B　第1章　ベクトル

	スライド	ノート
1. ベクトルと有向線分	[無料]
2. ベクトルの演算	[無料]
3. ベクトルの成分	[無料]
4. ベクトルの内積	[会員]
5. 位置ベクトル	[会員]
6. ベクトル方程式	[会員]
7. 平面ベクトルの応用	[会員]
8. 空間ベクトル	[会員]
9. 空間ベクトルの成分	[会員]
10. 空間ベクトルの内積	[会員]
11. 空間の位置ベクトル	[会員]
12. 空間ベクトルの応用	[会員]
13. 空間のベクトル方程式	[会員]