10. 空間ベクトルの内積(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学B　第1章　ベクトル

	スライド	ノート
1. ベクトルと有向線分	[無料]
2. ベクトルの演算	[無料]
3. ベクトルの成分	[無料]
4. ベクトルの内積	[会員]
5. 位置ベクトル	[会員]
6. ベクトル方程式	[会員]
7. 平面ベクトルの応用	[会員]
8. 空間ベクトル	[会員]
9. 空間ベクトルの成分	[会員]
10. 空間ベクトルの内積	[会員]
11. 空間の位置ベクトル	[会員]
12. 空間ベクトルの応用	[会員]
13. 空間のベクトル方程式	[会員]

10.　空間ベクトルの内積

10.1　空間ベクトルの内積

　空間内の$\overrightarrow{0}$でない2つのベクトル$\overrightarrow{\mathstrut a},\ \overrightarrow{b}$のなす角を$\theta$とすると，\[\overrightarrow{\mathstrut a}\cdot\overrightarrow{b}=|\overrightarrow{\mathstrut a}||\overrightarrow{b}|\cos\theta\ \ (0^\circ\leqq\theta\leqq180^\circ)\]

補足

　$\overrightarrow{\mathstrut a}=\overrightarrow{0}$，または$ \overrightarrow{b}=\overrightarrow{0}$のとき，$\overrightarrow{\mathstrut a}\cdot\overrightarrow{b}=0$と定義する．

10.2　内積と成分

　$\overrightarrow{\mathstrut a}=(a_1,\ a_2,\ a_3),\ \overrightarrow{\mathstrut b}=(b_1,\ b_2,\ b_3)$ のとき，
$[1]\ \ \overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}=a_1b_1+a_2b_2+a_3b_3$
$[2]\ \ \overrightarrow{\mathstrut a}\!\neq\!\overrightarrow{0}$，$\overrightarrow{\mathstrut b}\!\neq\!\overrightarrow{\mathstrut 0}$ のとき，$\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ のなす角を $\theta$ とすると， \[\begin{align*} \cos\theta&=\frac{\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}}{|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut b}|}\\ &=\frac{a_1b_1+a_2b_2+a_3b_3}{\sqrt{{a_1}^2+{a_2}^2+{a_3}^2}\sqrt{{b_1}^2+{b_2}^2+{b_3}^2}} \end{align*}\]

[1]の証明

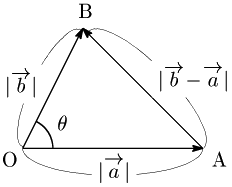
　余弦定理により，

AB$^2=$ OA$^2+$ OB$^2-2$ OA$\cdot$OB $\cos\theta$

\[\therefore |\overrightarrow{\mathstrut b}-\overrightarrow{\mathstrut a}|^2=|\overrightarrow{\mathstrut a}|^2+|\overrightarrow{\mathstrut b}|^2-2\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}\]

$\therefore \overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}=\dfrac{|\overrightarrow{\mathstrut a}|^2+|\overrightarrow{\mathstrut b}|^2-|\overrightarrow{\mathstrut b}-\overrightarrow{\mathstrut a}|^2}2\ \ \cdots$ ①

(①の右辺の分子)$=({a_1}^2\!+\!{a_2}^2\!+\!{a_3}^2)\!+\!({b_1}^2\!+\!{b_2}^2\!+\!{b_3}^2)$
　　　　　　　　　$-\{(b_1\!-\!a_1)^2\!+\!(b_2\!-\!a_2)^2\!+\!(b_3\!-\!a_3)^2\}$
　　　　　　　　$=2(a_1b_1+a_2b_2+a_3b_3)$

よって①より，

\[\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}=a_1b_1+a_2b_2+a_3b_3\]

■

例題　$\overrightarrow{a}=(-1,\ 2,\ -2),\ \overrightarrow{b}=(2,\ -2,\ 3)$の両方に垂直で，大きさが3であるベクトル$\overrightarrow{p}$を求めよ．

　$\overrightarrow{\mathstrut a}$，$\overrightarrow{\mathstrut b}$ の双方に垂直なベクトルの1つを $\overrightarrow{\mathstrut q}=(x,y,z)$ とすると，

　$\overrightarrow{\mathstrut q}\perp\overrightarrow{\mathstrut a}$ より $\overrightarrow{\mathstrut q}\cdot\overrightarrow{\mathstrut a}=0$
　　　$\therefore -x+2y-2z=0\ \ \cdots$ ①

　$\overrightarrow{\mathstrut q}\perp\overrightarrow{\mathstrut b}$ より $\overrightarrow{\mathstrut q}\cdot\overrightarrow{\mathstrut b}=0$
　　　$\therefore 2x-2y+3z=0\ \ \cdots$ ②

　①$+$② より，$x+z=0$　$\therefore x=-z\ \ \cdots$ ③
　①$\times2+$② より，$2y-z=0$　$\therefore y=\dfrac z2\ \ \cdots$ ④

　③，④ で $z=2$ とおくと，$\overrightarrow{\mathstrut q}=(-2,1,2)$

　よって， \[\begin{align*} \overrightarrow{\mathstrut p}&=\pm3\cdot\frac{\overrightarrow{\mathstrut q}}{|\overrightarrow{\mathstrut q}|}=\pm3\cdot\dfrac{(-2,1,2)}3\\[5pt] &=\underline{\boldsymbol{\pm(-2,1,2)}} \end{align*}\]

補足

　$\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ の双方に垂直なベクトルの1つを $\overrightarrow{\mathstrut q}$ とすると，次のような計算によって $\overrightarrow{\mathstrut q}$ を求めることができる．(詳しくはスライド(会員向け)参照．)

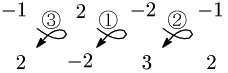
\[\begin{align*} \overrightarrow{\mathstrut q}&=\Bigl(2\!\cdot\!3\!-\!(-2)\!\cdot\!(-2),\ (-2)\!\cdot\!2\!-\!(-1)\!\cdot\!3,\ -1\!\cdot\!(-2)\!-\!2\!\cdot\!2\Bigr)\\[5pt] &=(2,\ -1,\ -2) \end{align*}\]

　実際，

\[\begin{align*} \overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut q}&=(-1,2,-2)\cdot(-2,1,2)=2+2-4=0\\[5pt] \overrightarrow{\mathstrut b}\cdot\overrightarrow{\mathstrut q}&=(2,-2,3)\cdot(-2,1,2)=-4-2+6=0\\[5pt] \end{align*}\]

となるから $\overrightarrow{\mathstrut a}\perp\overrightarrow{\mathstrut q}$ かつ $\overrightarrow{\mathstrut b}\perp\overrightarrow{\mathstrut q}$ である．

　$\overrightarrow{\mathstrut q}$ を $\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ の外積またはベクトル積という．ベクトル積は，2つのベクトルから1つのベクトルが返される．一方，内積は2つのベクトルから1つの実数が返される．従って内積のことをスカラー積ともいう．

10.3　内積の性質

\begin{align*} &[1]\ \ \overrightarrow{\mathstrut{a}}\cdot\overrightarrow{b}=\overrightarrow{b}\cdot\overrightarrow{\mathstrut{a}}\ \ (\mbox{交換法則})\\[5pt] &[2]\ \ \overrightarrow{a}\cdot\overrightarrow{a}=\left|\overrightarrow{a}\right|^2\\[5pt] &[3]\ \ \overrightarrow{\mathstrut{a}}\cdot(\overrightarrow{b}+\overrightarrow{\mathstrut{c}})=\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{b}+\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{\mathstrut{c}}\ \ (\mbox{分配法則})\\[5pt] &[4]\ \ (\overrightarrow{\mathstrut{a}}+\overrightarrow{b})\cdot\overrightarrow{\mathstrut{c}}=\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{\mathstrut{c}}+\overrightarrow{b}\cdot\overrightarrow{\mathstrut{c}}\ \ (\mbox{分配法則})\\[5pt] &[5]\ \ (k\overrightarrow{\mathstrut{a}})\cdot\overrightarrow{b}=\overrightarrow{a}\cdot(k\overrightarrow{b})=k(\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{b})\ \ (k\mbox{ は実数}) \end{align*}

補足

　平面ベクトルの内積の性質と完全に同一である．

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]

数学B　第1章　ベクトル

	スライド	ノート
1. ベクトルと有向線分	[無料]
2. ベクトルの演算	[無料]
3. ベクトルの成分	[無料]
4. ベクトルの内積	[会員]
5. 位置ベクトル	[会員]
6. ベクトル方程式	[会員]
7. 平面ベクトルの応用	[会員]
8. 空間ベクトル	[会員]
9. 空間ベクトルの成分	[会員]
10. 空間ベクトルの内積	[会員]
11. 空間の位置ベクトル	[会員]
12. 空間ベクトルの応用	[会員]
13. 空間のベクトル方程式	[会員]