高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | |
| 1. ベクトルと有向線分 | [無料] | |
| 2. ベクトルの演算 | [無料] | |
| 3. ベクトルの成分 | [無料] | |
| 4. ベクトルの内積 | [会員] | |
| 5. 位置ベクトル | [会員] | |
| 6. ベクトル方程式 | [会員] | |
| 7. 平面ベクトルの応用 | [会員] | |
| 8. 空間ベクトル | [会員] | |
| 9. 空間ベクトルの成分 | [会員] | |
| 10. 空間ベクトルの内積 | [会員] | |
| 11. 空間の位置ベクトル | [会員] | |
| 12. 空間ベクトルの応用 | [会員] | |
| 13. 空間のベクトル方程式 | [会員] |

2. ベクトルの演算
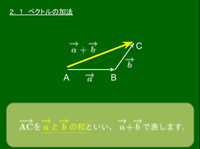
2.1 ベクトルの加法
$\overrightarrow{\mathstrut a}=\overrightarrow{\mathstrut\rm AB}$,$\overrightarrow{\mathstrut b}=\overrightarrow{\mathstrut\rm BC}$ のとき,$\overrightarrow{\mathstrut\rm AC}$ を $\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ の和といい, \[\overrightarrow{\mathstrut a}+\overrightarrow{\mathstrut b}\] で表す:
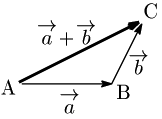
例
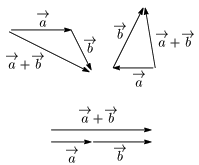
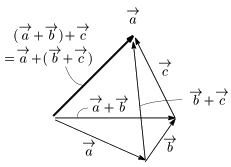
ベクトルの加法の性質\begin{align*} &[1]\ \overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}\ (\mbox{交換法則})\\ &[2]\ \ (\overrightarrow{a}\!+\!\overrightarrow{b})\!+\!\overrightarrow{c}\!=\!\overrightarrow{a}\!+\!(\overrightarrow{b}\!+\!\overrightarrow{c})\ (\mbox{結合法則}) \end{align*}
[1]
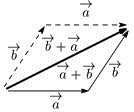
[2]
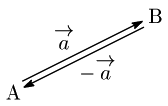
逆ベクトル
$\overrightarrow{\mathstrut a}$ と
大きさ:同じ
向き :反対
のベクトルを,$\overrightarrow{\mathstrut a}$ の逆ベクトルといい,$-\overrightarrow{\mathstrut a}$ で表す:
注意
ベクトルでは「$+,\,-$」は正負の意味ではなく,向きを表す.
零ベクトル
始点と終点が一致するベクトルを零ベクトルといい,$\overrightarrow{\mathstrut 0}$ で表す.
注意
$\overrightarrow{\mathstrut 0}$ の大きさは0,向きは考えない.
$-\overrightarrow{a}$と$\overrightarrow{0}$の性質\begin{align*} &[1]\hspace{5mm}\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{0}+\overrightarrow{a}=\overrightarrow{a}\\ &[2]\hspace{5mm}\overrightarrow{a}+(-\overrightarrow{a})=(-\overrightarrow{a})+\overrightarrow{a}=\overrightarrow{0} \end{align*}
[2]について
$\overrightarrow{\mathstrut a}=\overrightarrow{\mathstrut\rm AB}$ とすると,
\[\begin{align*} \overrightarrow{\mathstrut a}+(-\overrightarrow{\mathstrut a})&=\overrightarrow{\mathstrut\rm AB}+\overrightarrow{\mathstrut\rm BA}\\[5pt] &=\overrightarrow{\mathstrut\rm AA}\\[5pt] &=\overrightarrow{\mathstrut 0} \end{align*}\]
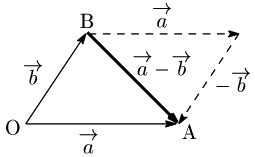
2.2 ベクトルの減法
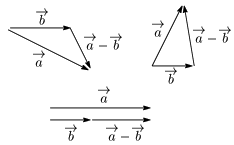
$\overrightarrow{\mathstrut a}+(-\overrightarrow{\mathstrut b})$ を $\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ の差といい, \[\overrightarrow{\mathstrut a}-\overrightarrow{\mathstrut b}\] で表す:
例

2.3 ベクトルの実数倍
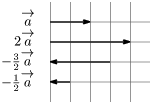
$\overrightarrow{\mathstrut a}$ と実数 $k$ に対して,$k\overrightarrow{\mathstrut a}$ を次のように定める:
1° $\overrightarrow{\mathstrut a}\neq\overrightarrow{\mathstrut 0}$ のとき
| $k>0$ | $k<0$ | |
| 大きさ | $|\overrightarrow{\mathstrut a}|$ の $k$ 倍 | $|\overrightarrow{\mathstrut a}|$ の $|k|$ 倍 |
| 向き | $\overrightarrow{\mathstrut a}$ と同じ | $\overrightarrow{\mathstrut a}$ と反対 |
また,$k=0$ のときは,$\overrightarrow{\mathstrut 0}$ と定める.
2° $\overrightarrow{\mathstrut a}=\overrightarrow{\mathstrut 0}$ のとき
任意の実数 $k$ に対して, \[k\overrightarrow{\mathstrut a}=\overrightarrow{\mathstrut 0}\] と定める.
例
ベクトルの実数倍の性質 $k,\ l$ が実数のとき,\begin{align*} &[1]\hspace{5mm}k(l\overrightarrow{a})=(kl)\overrightarrow{a}\\ &[2]\hspace{5mm}(k+l)\overrightarrow{a}=k\overrightarrow{a}+l\overrightarrow{a}\\ &[3]\hspace{5mm}k(\overrightarrow{a}+\overrightarrow{b})=k\overrightarrow{a}+k\overrightarrow{b} \end{align*}
[3]の証明
$k>0$ のとき
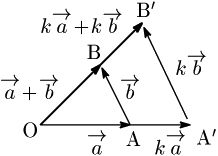
$\overrightarrow{\rm OB}$ と $\overrightarrow{\rm OB’}$ について,△OAB∽△OA$’$B$’$ により,
\[k|\overrightarrow{\rm OB}|=|\overrightarrow{\rm OB’}|\]
そして向きも同じであることから,
\[k\overrightarrow{\rm OB}=\overrightarrow{\rm OB’}\]
従って
\[k(\overrightarrow{\mathstrut a}+\overrightarrow{\mathstrut b})=k\overrightarrow{\mathstrut a}+k\overrightarrow{\mathstrut b}\]
が成り立つ.
$k<0$ の場合も同様にして示される.
補足
これまでの議論により,ベクトルの和,差,実数倍は,文字式と同じように扱えることがわかる.
例
$5\overrightarrow{a}+\overrightarrow{b}-(3\overrightarrow{a}+4\overrightarrow{b})=2\overrightarrow{a}-3\overrightarrow{b}$
$2(3\overrightarrow{a}-4\overrightarrow{b})=6\overrightarrow{a}-8\overrightarrow{b}$
2.4 ベクトルの平行
$\overrightarrow{\mathstrut 0}$ でない2つのベクトル $\overrightarrow{\mathstrut a}$,$\overrightarrow{\mathstrut b}$ について,向きが同じ,または反対のとき,「$\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ は平行である」といい, \[\overrightarrow{\mathstrut a}//\overrightarrow{\mathstrut b}\] で表す.
例
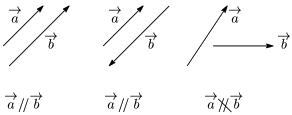
ベクトルの平行条件 $\overrightarrow{a}\neq\overrightarrow{0},\ \overrightarrow{b}\neq\overrightarrow{0}$ のとき,\[\overrightarrow{a}//\overrightarrow{b}\iff\overrightarrow{a}=k\overrightarrow{b}\ \ (k\mbox{は実数})\]
補足
$\dfrac{\overrightarrow{\mathstrut a}}{|\overrightarrow{\mathstrut a}|}$ は $\overrightarrow{\mathstrut a}$ と同じ向きに平行な単位ベクトルである.
∵)$\dfrac{\overrightarrow{\mathstrut a}}{|\overrightarrow{\mathstrut a}|}=\dfrac1{|\overrightarrow{\mathstrut a}|}\overrightarrow{\mathstrut a}$ であり,$\dfrac1{|\overrightarrow{\mathstrut a}|}>0$ により,$\overrightarrow{\mathstrut a}$ と同じ向き.
また,
\[\left|\frac{\overrightarrow{\mathstrut a}}{|\overrightarrow{\mathstrut a}|}\right|=\frac{|\overrightarrow{\mathstrut a}|}{|\overrightarrow{\mathstrut a}|}=1\]
により,単位ベクトル.
■
$\overrightarrow{a}\left(\neq\overrightarrow{0}\right)$ に平行な単位ベクトルは, \[\pm\frac{\overrightarrow{a}}{\ \left|\overrightarrow{a}\right|\ }\]
次の定理はベクトルの問題を解く上で今後何度も登場する.
重要な定理 $s,\ t,\ s’,\ t’$ を実数とする. $\overrightarrow{a}\neq\overrightarrow{0},\ \overrightarrow{b}\neq\overrightarrow{0}$で,$\overrightarrow{a}$と$\overrightarrow{b}$が平行でないとき, \begin{align*} s\overrightarrow{a}\!+\!t\overrightarrow{b}\!=\!s’\overrightarrow{a}\!+\!t’\overrightarrow{b}\iff s\!=\!s’,\, t\!=\!t’\ \cdots\mbox{①} \end{align*} 特に, \[s\overrightarrow{a}+t\overrightarrow{b}=\overrightarrow{0}\iff s=t=0\ \cdots\mbox{②}\]
証明
まず②を示す.
$\Leftarrow$ は明らか.
$\Rightarrow$
$s\neq0$ とすれば,$\overrightarrow{\mathstrut a}=-\dfrac ts \overrightarrow{\mathstrut b}$.
これは $\overrightarrow{\mathstrut a}//\overrightarrow{\mathstrut b}$ を意味し,矛盾.よって $s=0$.
このとき,$t\overrightarrow{\mathstrut b}=\overrightarrow{\mathstrut 0}$ となり,$\overrightarrow{\mathstrut b}\neq\overrightarrow{\mathstrut 0}$ により $t=0$.
■
次に①を示す.
$\Leftarrow$ は明らか.
$\Rightarrow$
変形して,
\[(s-s’)\overrightarrow{\mathstrut a}+(t-t’)\overrightarrow{\mathstrut b}=\overrightarrow{\mathstrut 0}\]
よって②より,
\[s-s’=0,\ \ t-t’=0\]
\[\therefore s=s’,\ \ t=t’\]
■
補足
$\overrightarrow{\mathstrut a}$,$\overrightarrow{\mathstrut b}$ がともに $\overrightarrow{\mathstrut 0}$ でなく,また平行でないとき,「$\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ は1次独立である」という.

2.5 ベクトルの分解
あるベクトル $\overrightarrow{\mathstrut p}$ が与えられると,1次独立な2つのベクトルの2方向に分解できる.
例
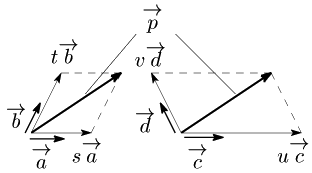
右は $\overrightarrow{\mathstrut p}\!=\!u\overrightarrow{\mathstrut c}\!+\!v\,\overrightarrow{\mathstrut d}$
($s,t,u,v$ は実数)
$\overrightarrow{\mathstrut p}$ を $s\overrightarrow{\mathstrut a}\!+\!t\overrightarrow{\mathstrut b}$ のように表すとき,これをベクトルの分解という.
任意のベクトル $\overrightarrow{\mathstrut p}$ に対して, \[\overrightarrow{\mathstrut p}=s\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut b}\] と表せるとき,上の定理 により実数 $s,t$ は $\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ に応じてただ1通りに決定する.即ち, \[\left\{\begin{array}{l} \overrightarrow{\mathstrut a}=s\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut b}\\[5pt] \overrightarrow{\mathstrut a}=s’\overrightarrow{\mathstrut a}+t’\overrightarrow{\mathstrut b} \end{array}\right.\] のような見かけ上異なる表現が取れたとしても実際は \[s=s’,\ \ \ t=t’\] である.
ベクトルの分解 2つのベクトル $\overrightarrow{\mathstrut a}$,$\overrightarrow{\mathstrut b}$ は$\overrightarrow{\mathstrut 0}$ ではなく,また平行でもないとする.このとき,任意のベクトル $\overrightarrow{\mathstrut p}$ は実数 $s,t$ を用いて, \[\overrightarrow{\mathstrut p}=s\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut b}\] とただ1通りに表現できる.
補足
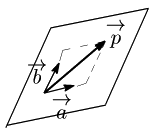
逆に1次独立な2つのベクトル $\overrightarrow{\mathstrut a}$,$\overrightarrow{\mathstrut b}$ を決めると,$\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ で張る平面上の任意のベクトル $\overrightarrow{\mathstrut p}$ は,実数 $s,t$ を用いて, \[\overrightarrow{\mathstrut p}=s\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut b}\] の形でただ1通りに表すことができる.

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | |
| 1. ベクトルと有向線分 | [無料] | |
| 2. ベクトルの演算 | [無料] | |
| 3. ベクトルの成分 | [無料] | |
| 4. ベクトルの内積 | [会員] | |
| 5. 位置ベクトル | [会員] | |
| 6. ベクトル方程式 | [会員] | |
| 7. 平面ベクトルの応用 | [会員] | |
| 8. 空間ベクトル | [会員] | |
| 9. 空間ベクトルの成分 | [会員] | |
| 10. 空間ベクトルの内積 | [会員] | |
| 11. 空間の位置ベクトル | [会員] | |
| 12. 空間ベクトルの応用 | [会員] | |
| 13. 空間のベクトル方程式 | [会員] |