12. 空間ベクトルの応用(ノート)
スライドで学ぶ高校数学

このページにある内容は，こちらのスライド でわかり易く説明しています．

PC環境なら全画面表示でより見やすく，よりわかりやすい！
全画面表示の仕方は こちら

高校数学[総目次]

数学B　第1章　ベクトル

12.　空間ベクトルの応用

12.1　一直線上の3点

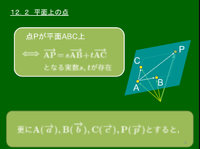
12.2　平面上の点

　空間内の一直線上にない3点A，B，Cが与えられると，それら3点を含む平面が存在し，かつそのような平面はただ1つである．この平面を平面ABCという．

　平面上の点Pについては次が重要：

　${\rm A}(\overrightarrow{\mathstrut{a}})$，${\rm B}(\overrightarrow{b})$，${\rm C}(\overrightarrow{\mathstrut{c}})$，${\rm P}(\overrightarrow{\mathstrut{p}})$ とすると，上の式は

$$\overrightarrow{\mathstrut{p}}-\overrightarrow{\mathstrut{a}}=s(\overrightarrow{b}-\overrightarrow{\mathstrut{a}})+t(\overrightarrow{\mathstrut{c}}-\overrightarrow{\mathstrut{a}})$$

$$\therefore \overrightarrow{\mathstrut{p}}=(1-s-t)\overrightarrow{\mathstrut{a}}+s\overrightarrow{b}+t\overrightarrow{\mathstrut{c}}$$

　ここで，$1-s-t=r$ とおくと，

$$\overrightarrow{\mathstrut{p}}=r\overrightarrow{\mathstrut{a}}+s\overrightarrow{b}+t\overrightarrow{\mathstrut{c}}\ \ \ (r+s+t=1)$$

　$\overrightarrow{\mathstrut{p}}$ がこのように表されるとき，この表し方はただ1通りであり，次が成立：

例題　図のような直方体において，DEの延長上に DE$=$EF となる点Fをとる．直線OFと平面ABCの交点をPとするとき，$\overrightarrow{\rm OP}$ を $\overrightarrow{\rm OA}$，$\overrightarrow{\rm OB}$，$\overrightarrow{\rm OC}$ で表せ．

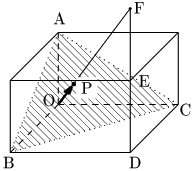
答

$$\begin{align*} \overrightarrow{\mathstrut{\rm{OF}}}&=\overrightarrow{\mathstrut{\rm{OB}}}+\overrightarrow{\mathstrut{\rm{BD}}}+\overrightarrow{\mathstrut{\rm{DF}}}\\[5pt] &=\overrightarrow{\mathstrut{\rm{OB}}}+\overrightarrow{\mathstrut{\rm{OC}}}+2\overrightarrow{\mathstrut{\rm{OA}}} \end{align*}$$

　従って，

$$\begin{align*} \overrightarrow{\mathstrut{\rm{OP}}}&=k\,\overrightarrow{\mathstrut{\rm{OF}}}\\[5pt] &=k\left(\overrightarrow{\mathstrut{\rm{OB}}}+\overrightarrow{\mathstrut{\rm{OC}}}+2\overrightarrow{\mathstrut{\rm{OA}}}\right)\\[5pt] &=2k\,\overrightarrow{\mathstrut{\rm{OA}}}+k\,\overrightarrow{\mathstrut{\rm{OB}}}+k\,\overrightarrow{\mathstrut{\rm{OC}}}\\[5pt] \end{align*}$$

　点Pは平面ABC上にあるから，

$$2k+k+k=1\ \ \therefore k=\frac14$$

　よって，

$$\underline{\boldsymbol{\overrightarrow{\mathstrut{\rm{OP}}}=\frac12\overrightarrow{\mathstrut{\rm{OA}}}+\frac14\overrightarrow{\mathstrut{\rm{OB}}}+\frac14\overrightarrow{\mathstrut{\rm{OC}}}}}$$

高校数学[総目次]

数学B　第1章　ベクトル