9. 空間ベクトルの成分(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学B　第1章　ベクトル

	スライド	ノート
1. ベクトルと有向線分	[無料]
2. ベクトルの演算	[無料]
3. ベクトルの成分	[無料]
4. ベクトルの内積	[会員]
5. 位置ベクトル	[会員]
6. ベクトル方程式	[会員]
7. 平面ベクトルの応用	[会員]
8. 空間ベクトル	[会員]
9. 空間ベクトルの成分	[会員]
10. 空間ベクトルの内積	[会員]
11. 空間の位置ベクトル	[会員]
12. 空間ベクトルの応用	[会員]
13. 空間のベクトル方程式	[会員]

9.　空間ベクトルの成分

9.1　空間ベクトルの成分

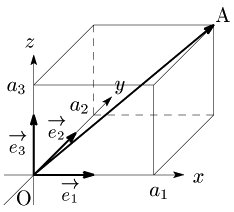
　空間内の任意のベクトルは，始点が原点Oにくるように平行移動したときの終点が A$(a_1,a_2,a_3)$ とすれば，図のような大きさ1の3つのベクトル $\overrightarrow{\mathstrut e_1}$，$\overrightarrow{\mathstrut e_2}$，$\overrightarrow{\mathstrut e_3}$ (基本ベクトル) を用いて，

\[\overrightarrow{\mathstrut\rm OA}=a_1\overrightarrow{\mathstrut e_1}+a_2\overrightarrow{\mathstrut e_2}+a_3\overrightarrow{\mathstrut e_3}\]

と表せる．よって平面のときと同様に

\[\overrightarrow{\mathstrut\rm OA}=(a_1,\ a_2,\ a_3)\]

と表すことができて，これを空間ベクトルの成分表示という．

9.2　空間ベクトルの相等

$\overrightarrow{a}=(a_1,\ a_2,\ a_3),\ \overrightarrow{b}=(b_1,\ b_2,\ b_3)$のとき，\[\overrightarrow{a}=\overrightarrow{b}\iff a_1=b_1,\ a_2=b_2,\ a_3=b_3\]

9.3　空間ベクトルの和・差・実数倍

$\overrightarrow{a}=(a_1,\ a_2,\ a_3),\ \overrightarrow{b}=(b_1,\ b_2,\ b_3)$のとき，\begin{align*}&[1]\ \ (a_1,a_2,a_3)\!+\!(b_1,b_2,b_3)\!=\!(a_1\!+\!b_1,a_2\!+\!b_2,a_3\!+\!b_3)\\[5pt] &[2]\ \ k(a_1,\ a_2,\ a_3)=(ka_1,\ ka_2,\ ka_3)\ \ (k\mbox{は実数})\end{align*}

9.4　$\overrightarrow{\rm{AB}}$の成分と大きさ

　2点A$(a_1,\ a_2,\ a_3),\ \rm{B}(b_1,\ b_2,\ b_3)$について，\begin{align*}&\overrightarrow{\rm{AB}}=(b_1-a_1,\ b_2-a_2,\ b_3-a_3)\\[5pt] &|\overrightarrow{\rm{AB}}|=\sqrt{(b_1-a_1)^2+(b_2-a_2)^2+(b_3-a_3)^2}\end{align*}

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]

数学B　第1章　ベクトル

	スライド	ノート
1. ベクトルと有向線分	[無料]
2. ベクトルの演算	[無料]
3. ベクトルの成分	[無料]
4. ベクトルの内積	[会員]
5. 位置ベクトル	[会員]
6. ベクトル方程式	[会員]
7. 平面ベクトルの応用	[会員]
8. 空間ベクトル	[会員]
9. 空間ベクトルの成分	[会員]
10. 空間ベクトルの内積	[会員]
11. 空間の位置ベクトル	[会員]
12. 空間ベクトルの応用	[会員]
13. 空間のベクトル方程式	[会員]