11. 空間の位置ベクトル(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学B　第1章　ベクトル

	スライド	ノート
1. ベクトルと有向線分	[無料]
2. ベクトルの演算	[無料]
3. ベクトルの成分	[無料]
4. ベクトルの内積	[会員]
5. 位置ベクトル	[会員]
6. ベクトル方程式	[会員]
7. 平面ベクトルの応用	[会員]
8. 空間ベクトル	[会員]
9. 空間ベクトルの成分	[会員]
10. 空間ベクトルの内積	[会員]
11. 空間の位置ベクトル	[会員]
12. 空間ベクトルの応用	[会員]
13. 空間のベクトル方程式	[会員]

11.　空間の位置ベクトル

11.1　位置ベクトル

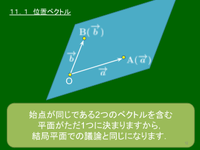
　空間内に1点Oを固定する．
　空間内の任意の点Pの位置は， \[\overrightarrow{\mathstrut p}=\overrightarrow{\mathstrut\rm OP}\] というベクトルで決まる．このとき，$\overrightarrow{\mathstrut p}$ を点Oに関する点Pの位置ベクトルといい，位置ベクトルが $\overrightarrow{\mathstrut p}$ である点Pを ${\rm P}(\overrightarrow{\mathstrut p})$ で表す．

　平面の場合と同様に，2点 ${\rm A}(\overrightarrow{\mathstrut a})$，${\rm B}(\overrightarrow{\mathstrut b})$ について，次が成り立つ：

　2点 A$(\overrightarrow{a}),\ {\rm B}(\overrightarrow{b})$ について，\[\overrightarrow{\rm{AB}}=\overrightarrow{b}-\overrightarrow{a}\]

11.2　分点の位置ベクトル

内分点，外分点の位置ベクトル　2点${\rm A}(\overrightarrow{a}),\ {\rm B}(\overrightarrow{b})$について，線分ABを\begin{align*} &m:n\mbox{に内分する点P}(\overrightarrow{p}):\hspace{4mm}\overrightarrow{p}=\frac{n\overrightarrow{a}+m\overrightarrow{b}}{m+n}\\[5pt] &m:n\mbox{に外分する点Q}(\overrightarrow{q}):\hspace{4mm}\overrightarrow{q}=\frac{-n\overrightarrow{a}+m\overrightarrow{b}}{m-n}\end{align*}　特に，線分ABの中点Mの位置ベクトル$\overrightarrow{m}$は\[\overrightarrow{m}=\frac{\overrightarrow{a}+\overrightarrow{b}}2\]

補足

　平面ベクトルの場合と完全に同一である．

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]

数学B　第1章　ベクトル

	スライド	ノート
1. ベクトルと有向線分	[無料]
2. ベクトルの演算	[無料]
3. ベクトルの成分	[無料]
4. ベクトルの内積	[会員]
5. 位置ベクトル	[会員]
6. ベクトル方程式	[会員]
7. 平面ベクトルの応用	[会員]
8. 空間ベクトル	[会員]
9. 空間ベクトルの成分	[会員]
10. 空間ベクトルの内積	[会員]
11. 空間の位置ベクトル	[会員]
12. 空間ベクトルの応用	[会員]
13. 空間のベクトル方程式	[会員]