このページにある内容は，こちらのスライド でわかり易く説明しています．

PC環境なら全画面表示でより見やすく，よりわかりやすい！
全画面表示の仕方は こちら

高校数学[総目次]

数学B　第1章　ベクトル

  スライド ノート
1. ベクトルと有向線分 [無料]  
2. ベクトルの演算 [無料]  
3. ベクトルの成分 [無料]  
4. ベクトルの内積 [会員]  
5. 位置ベクトル [会員]  
6. ベクトル方程式 [会員]  
7. 平面ベクトルの応用 [会員]  
8. 空間ベクトル [会員]  
9. 空間ベクトルの成分 [会員]  
10. 空間ベクトルの内積 [会員]  
11. 空間の位置ベクトル [会員]  
12. 空間ベクトルの応用 [会員]  
13. 空間のベクトル方程式 [会員]  

1．ベクトルと有向線分

1.1　ベクトルとは

ベクトルとは？

「大きさ」と「向き」をもった量

例　(物理)

　力　　：右向きに5[N]
　速度　：北向きに4m/s
　加速度：下向きに9.8m/s$^2$

補足

　大きさのみをもった量をスカラーという．
　例　速さ（＝速度の大きさ）

1.2　有向線分

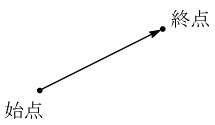
　始点と終点を指定した線分を有向線分という．
　　→　矢印で表すことができる．

　ベクトルは有向線分で表すことができる．このとき，

  1. ベクトルの
    　大きさ：有向線分の長さで表す．
    　向き　：有向線分の向きで表す．
  2. 有向線分の位置は問題にしない．
    →　平行移動して重なるものはベクトルとしては同じ．

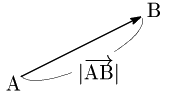
　Aを始点，Bを終点とする有向線分を，$\overrightarrow{\mathstrut\rm AB}$ で表し，その大きさを $|\overrightarrow{\mathstrut\rm AB}|$ で表す．また，1文字で $\overrightarrow{\mathstrut a}$，$|\overrightarrow{\mathstrut a}|$ と表すことも多い．

　大きさと向きが等しい2つのベクトル $\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ は \[\overrightarrow{\mathstrut a}=\overrightarrow{\mathstrut b}\] と表す．

注意

　$|\overrightarrow{\mathstrut a}|$ は「$\overrightarrow{\mathstrut a}$ の大きさ」と読み，「$\overrightarrow{\mathstrut a}$ の絶対値」とは言わない．

よくある質問

なぜ矢印(有向線分)が登場するのですか？ベクトルと矢印はどういう関係ですか？

矢印(有向線分)という図形が、向きと大きさをもつ量(つまりベクトル)を表すものとして最適だから．

　ベクトルについて「大きさと向きをもった量をベクトルという」と説明されても，この表現はきわめて抽象的であって，とりわけ初学者にとっては何のことだかさっぱりわからない．しかし矢印(有向線分)はとても身近な図形である上に，ベクトルという得体の知れないものを具体的に目に見える形として表現するのにピッタリな素材なのである．加えてベクトル単体の表現にとどまらず，次節以降で学ぶベクトルの和や差，実数倍といったものも，有向線分で視覚的に理解することができる．
　大きさと向きを同時に表すことができる図形は有向線分(矢印)以外でも考えることはできる．そういった図形を集めてきて，どれがベクトルを表すのに最もふさわしいかというコンテストを行えば，表現の簡便さ，演算との親和性等から有向線分が優勝することはほぼ間違いない．

単位ベクトル

　大きさが1のベクトルを単位ベクトルという．単位ベクトルは大きさだけを問題にしており，向きは問わない．

このページで疑問は解決されましたか？

　こちら から数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]

数学B　第1章　ベクトル

  スライド ノート
1. ベクトルと有向線分 [無料]  
2. ベクトルの演算 [無料]  
3. ベクトルの成分 [無料]  
4. ベクトルの内積 [会員]  
5. 位置ベクトル [会員]  
6. ベクトル方程式 [会員]  
7. 平面ベクトルの応用 [会員]  
8. 空間ベクトル [会員]  
9. 空間ベクトルの成分 [会員]  
10. 空間ベクトルの内積 [会員]  
11. 空間の位置ベクトル [会員]  
12. 空間ベクトルの応用 [会員]  
13. 空間のベクトル方程式 [会員]