高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | |
| 1. ベクトルと有向線分 | [無料] | |
| 2. ベクトルの演算 | [無料] | |
| 3. ベクトルの成分 | [無料] | |
| 4. ベクトルの内積 | [会員] | |
| 5. 位置ベクトル | [会員] | |
| 6. ベクトル方程式 | [会員] | |
| 7. 平面ベクトルの応用 | [会員] | |
| 8. 空間ベクトル | [会員] | |
| 9. 空間ベクトルの成分 | [会員] | |
| 10. 空間ベクトルの内積 | [会員] | |
| 11. 空間の位置ベクトル | [会員] | |
| 12. 空間ベクトルの応用 | [会員] | |
| 13. 空間のベクトル方程式 | [会員] |

6.ベクトル方程式
等式には方程式と恒等式があって,方程式とは特定の値でのみ成立する等式,恒等式とはいかなる値でも成立する等式である.方程式の例としては $y=2x+3$ などで,この方程式を満たす $(x,\ y)$ の組として $(0,\ 3)$,$(1,\ 5)$ などがあり,すべての組を座標平面上に取っていくと,そこに現れる図形は直線である.このような方程式をベクトルにまで拡張しよう.
6.1 直線のベクトル方程式
直線のベクトル方程式は,ちょっとした思考の転換が必要
これからベクトルによって直線を表そうという訳だが,これまでの $y=mx+n$ の形が頭にあると,かえって理解の邪魔になるかもしれない.$y=mx+n$ は
$x$ が決まる → $y$ が決まる → 点 $(x,\ y)$ が決まる
という流れであり,従って方程式の左辺は「$y=$」となっている場合が多い.一方,ベクトルで直線を表すときには
$t$ が決まる → 点 $(x,\ y)$ が決まる
といったように, $x,\ y$ の文字以外に点を動かす原動力となる実数 $t$ を介在させている.その結果ベクトル方程式では直線上の点を表す位置ベクトル $\overrightarrow{\mathstrut p}$ が左辺にくる場合が多い.
このように,ベクトルで直線を表現するには従来とやや異なった思考が必要である.
ではどのようにベクトルで直線を表現するのか
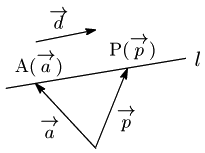
直線 $l$ は点Aを通るとし,その位置ベクトルを $\overrightarrow{\mathstrut a}$,また直線の向きを表すベクトルを $\overrightarrow{\mathstrut d}(\neq\overrightarrow{\mathstrut 0})$ とする.この直線上に点Pがあり,その位置ベクトルを $\overrightarrow{\mathstrut p}=(x,\ y)$ とすると
$\overrightarrow{\mathstrut{\rm AP}}=\overrightarrow{\mathstrut 0}$ または $\overrightarrow{\mathstrut{\rm AP}}\ //\ \overrightarrow{\mathstrut d}$
であるから,
点Pが $l$ 上
$\iff \overrightarrow{\mathstrut{\rm AP}}=t\overrightarrow{\mathstrut d}$ となる実数 $t$ が存在
が成り立つ.$\overrightarrow{\mathstrut{\rm AP}}=\overrightarrow{\mathstrut p}-\overrightarrow{\mathstrut a}$ より, \[\overrightarrow{\mathstrut p}-\overrightarrow{\mathstrut a}=t\overrightarrow{\mathstrut d}\] \[\therefore \overrightarrow{\mathstrut p}=\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut d}\] これを,点$\boldsymbol{{\rm A}(\overrightarrow{\mathstrut a})}$ を通り,$\boldsymbol{\overrightarrow{\mathstrut d}}$ に平行な直線のベクトル方程式といい,$t$ を媒介変数,$\overrightarrow{\mathstrut d}$ を方向ベクトルという.
直線のベクトル方程式点${\rm A}(\overrightarrow{\mathstrut a})$ を通り,$\overrightarrow{\mathstrut d}(\neq\overrightarrow{\mathstrut 0})$ に平行な直線上の点を ${\rm P}(\overrightarrow{\mathstrut p})$ とすると,この直線のベクトル方程式は\[\overrightarrow{\mathstrut p}=\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut d}\]

$t$ を$-0.5$ から $1.5$ まで
変化させたときの,点Pの動き方
補足
見た目が異なるので直線に見えない…でも中身は同じ
私たちは $y=mx+n$ の形を直線と理解してきたので,ベクトル方程式を見るとにわかにそれが直線を表しているようには見えない.しかし見た目は全く異なっているものの中身は同じで,双方向に変換も可能である.
1つだけ例を挙げると,直線 $y=\dfrac32x+1$ について,直線上の点で例えば A$(2,\ 4)$ をとると,$\overrightarrow{\mathstrut a}=(2,4)$,また傾きが $\dfrac32$ だから方向ベクトル $\overrightarrow{\mathstrut d}=(2,\ 3)$,直線上の点を表す位置ベクトルを $\overrightarrow{\mathstrut p}=(x,\ y)$ とすれば,
\[\overrightarrow{\mathstrut p}=\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut d}\]
と表せる.逆に,$\overrightarrow{\mathstrut p}=\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut d}$ のとき
\[\begin{align*} \overrightarrow{\mathstrut p}&=\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut d}\\[5pt] (x,\ y)&=(2,\ 4)+t(2,\ 3) \end{align*}\] \[\therefore \left\{\begin{array}{ll} x=2+2t&\cdots\ \mbox{①}\\[5pt] y=4+3t&\cdots\ \mbox{②} \end{array}\right.\]
①×3-②×2 から $t$ を消去すると,
\[3x-2y=-2\ \ \therefore y=\dfrac32+1\]
となって元の方程式が得られる.
注意
方向ベクトルは実数倍の任意性がある
すぐ上で上げた例では方向ベクトルとして $\overrightarrow{\mathstrut d}=(2,\ 3)$ をとったが,直線の向きを表すものなら $\overrightarrow{\mathstrut d}=(2,\ 3)$ と平行なものなら何でもよいはずで,例えば
\[\overrightarrow{\mathstrut d}=(2,\ 3)\,//\,(4,\ 6)\,//\,(-2,\ -4)\,//\,\cdots\]
など方向ベクトルはただ1つには定まらず,実数倍されたもの(ただし0倍は除く)はどれでもその直線の方向ベクトルとして採用してよい.
例題 点(2,1)を通り,$\overrightarrow{d}=(4,3)$ に平行な直線と,$y$ 軸との交点の座標を求めよ.
$\overrightarrow{\mathstrut p}=(x,y)$ とすると, \[(x,y)=(2,1)+t(4,3)\] \[\therefore\ \left\{\begin{array}{l} x=2+4t\\[5pt] y=1+3t \end{array}\right.\ \cdots\mbox{①}\] $x=0$ のとき,$0=2+4t$. $\therefore t=-\dfrac12$.
このとき $y=1+3\cdot\left(-\dfrac12\right)=-\dfrac12$.
よって,直線は $y$ 軸と $\underline{\boldsymbol{\left(0,-\dfrac12\right)}}$ で交わる.
補足
①の2式より $t$ を消去すると,$3x-4y-2=0$ が得られる.

6.2 2点を通る直線のベクトル方程式
通る2点がわかれば直線は決定する
数学Ⅱの図形と方程式 では,直線が通る2点 $(x_1,\ y_1)$,$(x_2,\ y_2)$ がわかれば
\[y-y_1=\dfrac{y_2-y_1}{x_2-x_1}(x-x_1)\]
という具合に方程式を導くことができた.ベクトルでも直線上の2点を表す位置ベクトルがわかれば方程式を導くことができる.
2点 ${\rm A}(\overrightarrow{\mathstrut a})$,${\rm B}(\overrightarrow{\mathstrut b})$ を通る直線は,方向ベクトルが $\overrightarrow{\mathstrut\rm AB}(=\overrightarrow{\mathstrut b}-\overrightarrow{\mathstrut a})$ であると考えて, \[\begin{align*} \overrightarrow{\mathstrut p}&=\overrightarrow{\mathstrut a}+t(\overrightarrow{\mathstrut b}-\overrightarrow{\mathstrut a})\\[5pt] &=(1-t)\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut b} \end{align*}\] ここで $1-t=s$ とおくと,$s+t=1$であり, \[\overrightarrow{\mathstrut p}=s\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut b}\] と表せる.
まとめ 2点A$(\overrightarrow{a}),\ $B$(\overrightarrow{b})$ を通る直線のベクトル方程式は,\[\overrightarrow{p}=(1-t)\overrightarrow{a}+t\overrightarrow{b}\] または,\[\overrightarrow{p}=s\overrightarrow{a}+t\overrightarrow{b}\ \ (\mbox{ただし}\,s+t=1) \]
補足
$s$ と $t$ に制限がなければ平面全体,$s+t=1$ で直線
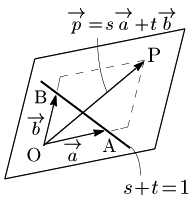
$\overrightarrow{\mathstrut a}$ と $\overrightarrow{\mathstrut b}$ で張る平面上の任意の点P$(\overrightarrow{\mathstrut p})$ は,$s,t$ を実数として \[\overrightarrow{\mathstrut p}=s\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut b}\] と1通りに表せるが,ここに $s+t=1$ という条件が加わると,Pは直線AB上にしか存在できない.
定理 $\overrightarrow{\rm{OP}}=s\overrightarrow{\rm{OA}}\!+\!t\overrightarrow{\rm{OB}}\ (s,\ t\ $ は実数) で与えられる点Pについて,\[\mbox{Pが直線AB上}\iff s+t=1\]

6.3 法線ベクトルと直線
直線に垂直なベクトルを用いた直線の表現
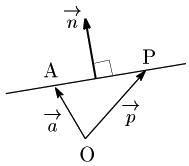
点 ${\rm A}(\overrightarrow{\mathstrut a})$ を通り,$\overrightarrow{\mathstrut n}(\neq\overrightarrow{\mathstrut 0})$ に垂直な直線上の点を ${\rm P}(\overrightarrow{\mathstrut p})$ とする.
このとき,
$\overrightarrow{\mathstrut n}\perp\overrightarrow{\mathstrut\rm AP}$ または $\overrightarrow{\mathstrut\rm AP}=\overrightarrow{\mathstrut 0}$
により,$\overrightarrow{\mathstrut n}\cdot\overrightarrow{\mathstrut\rm AP}=0$ であるから
\[\overrightarrow{\mathstrut n}\cdot(\overrightarrow{\mathstrut p}-\overrightarrow{\mathstrut a})=0\]
これを,点A$\boldsymbol{(\overrightarrow{a})}$ を通り,$\boldsymbol{\overrightarrow{n}}$ に垂直な直線のベクトル方程式という.また,$\overrightarrow{\mathstrut n}$ のように,直線と垂直なベクトルをその直線の法線ベクトルという.
まとめ 点A$(\overrightarrow{a})$を通り,$\overrightarrow{n}$に垂直な直線のベクトル方程式は,\[\overrightarrow{n}\cdot(\overrightarrow{p}-\overrightarrow{a})=0\]
この表現では媒介変数が必要ない
最初に出てきた直線のベクトル方程式は $\overrightarrow{\mathstrut p}=\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut d}$ といったように媒介変数 $t$ が必要であったが,この表現では媒介変数は必要ない.その理由は,前者が
$\overrightarrow{\rm AP}$ と $\overrightarrow{\mathstrut d}$ が平行
$\iff\overrightarrow{\rm AP}=t\,\overrightarrow{\mathstrut d}$ となる実数 $\boldsymbol t$ が存在
というようにベクトルの平行条件を元にして導いたのに対して,後者は
$\overrightarrow{\rm AP}\perp \overrightarrow{\mathstrut n} \iff\overrightarrow{\rm AP}\cdot\overrightarrow{\mathstrut n}=0$
というようにベクトルの垂直条件を元にして導いたためである.
この表現も $ax+by+c=0$ と双方向に変換が可能
上の式が直線を表していることを確かめてみよう.
$\overrightarrow{\mathstrut a}=(x_1,y_1)$,$\overrightarrow{\mathstrut n}=(a,b)$,$\overrightarrow{\mathstrut p}=(x,y)$ とすると,上の式は
\[\begin{align*}
(a,b)\cdot(x-x_1,\ y-y_1)&=0\\[5pt]
\therefore a(x-x_1)+b(y-y_1)&=0\\[5pt]
\therefore ax+by-ax_1-by_1&=0
\end{align*}\]
従って,この式は直線を表す.
逆に直線 $ax+by+c=0$ が与えられると,$\overrightarrow{\mathstrut n}=(a,b)$ はこの直線の法線ベクトル となる.
直線の法線ベクトル 直線 $ax+by+c=0$ について,\[\overrightarrow{\mathstrut n}=(a,\ b)\]はこの直線の法線ベクトルである.
注意
方向ベクトルと同様に,法線ベクトルも実数倍の任意性がある.
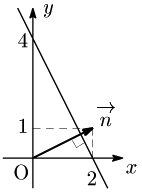
例
直線 $2x+y-4=0$ $(y=-2x+4)$ について,$\overrightarrow{\mathstrut n}=(2,1)$ はこの直線の法線ベクトルとなる.

6.4 円のベクトル方程式
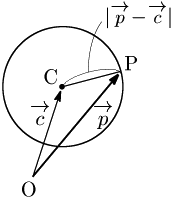
中心 ${\rm C}(\overrightarrow{\mathstrut c})$,半径 $r$ の円周上の点 ${\rm P}(\overrightarrow{\mathstrut p})$ は, \[|\overrightarrow{\mathstrut\rm CP}|=r\] を満たす.故に, \[|\overrightarrow{\mathstrut p}-\overrightarrow{\mathstrut c}|=r\] これを 中心 $\boldsymbol{{\rm C}(\overrightarrow{\mathstrut c})}$,半径 $\boldsymbol{r}$ の円のベクトル方程式 という.
円のベクトル方程式 点 ${\rm C}(\overrightarrow{\mathstrut c})$ を中心とし,半径を $r$ とする円のベクトル方程式は, \[|\overrightarrow{\mathstrut p}-\overrightarrow{\mathstrut c}|=r\]
円の方程式でも双方向に変換が可能
上の式から,数学Ⅱの円の方程式 で学んだ $xy$ 平面上の円の方程式を導いてみよう.
$\overrightarrow{\mathstrut p}=(x,y)$,$\overrightarrow{\mathstrut c}=(a,b)$ とおくと,上の式は \[\begin{align*} |(x-a,\ y-b)|&=r\\[5pt] \therefore \sqrt{(x-a)^2+(y-b)^2}&=r\\[5pt] \therefore (x-a)^2+(y-b)^2&=r^2 \end{align*}\]
この計算の逆をたどれば,円のベクトル方程式が得られる.
2点を直径の両端とする円
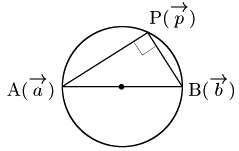
2点 ${\rm A}(\overrightarrow{\mathstrut a})$,${\rm B}(\overrightarrow{\mathstrut b})$を直径の両端とする円周上の点を ${\rm P}(\overrightarrow{\mathstrut p})$ とすると,
$\overrightarrow{\mathstrut\rm AP}\perp\overrightarrow{\mathstrut\rm BP}$ または $\overrightarrow{\mathstrut\rm AP}=\overrightarrow{\mathstrut 0}$ または $\overrightarrow{\mathstrut\rm BP}=\overrightarrow{\mathstrut 0}$
であるから, \[\overrightarrow{\mathstrut\rm AP}\cdot\overrightarrow{\mathstrut\rm BP}=0\] \[\therefore (\overrightarrow{\mathstrut p}-\overrightarrow{\mathstrut a})\cdot(\overrightarrow{\mathstrut p}-\overrightarrow{\mathstrut b})=0\]
2点 ${\rm A}(\overrightarrow{\mathstrut a})$,${\rm B}(\overrightarrow{\mathstrut b})$を直径の両端とする円のベクトル方程式は, \[(\overrightarrow{\mathstrut p}-\overrightarrow{\mathstrut a})\cdot(\overrightarrow{\mathstrut p}-\overrightarrow{\mathstrut b})=0\]
この式が円を表すことを確かめよう.
中心の位置ベクトル $:\dfrac{\overrightarrow{\mathstrut a}+\overrightarrow{\mathstrut b}}2$
半径 $:\dfrac{|\overrightarrow{\mathstrut a}-\overrightarrow{\mathstrut b}|}2$
よって,
■

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | |
| 1. ベクトルと有向線分 | [無料] | |
| 2. ベクトルの演算 | [無料] | |
| 3. ベクトルの成分 | [無料] | |
| 4. ベクトルの内積 | [会員] | |
| 5. 位置ベクトル | [会員] | |
| 6. ベクトル方程式 | [会員] | |
| 7. 平面ベクトルの応用 | [会員] | |
| 8. 空間ベクトル | [会員] | |
| 9. 空間ベクトルの成分 | [会員] | |
| 10. 空間ベクトルの内積 | [会員] | |
| 11. 空間の位置ベクトル | [会員] | |
| 12. 空間ベクトルの応用 | [会員] | |
| 13. 空間のベクトル方程式 | [会員] |

