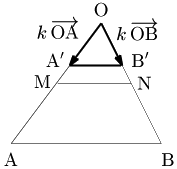7. 平面ベクトルの応用(ノート)

高校数学ノート[総目次]

数学B　第1章　ベクトル

	スライド	ノート
1. ベクトルと有向線分	[無料]
2. ベクトルの演算	[無料]
3. ベクトルの成分	[無料]
4. ベクトルの内積	[会員]
5. 位置ベクトル	[会員]
6. ベクトル方程式	[会員]
7. 平面ベクトルの応用	[会員]
8. 空間ベクトル	[会員]
9. 空間ベクトルの成分	[会員]
10. 空間ベクトルの内積	[会員]
11. 空間の位置ベクトル	[会員]
12. 空間ベクトルの応用	[会員]
13. 空間のベクトル方程式	[会員]

7．平面ベクトルの応用

7.1　線分上の点の存在範囲

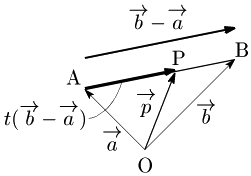
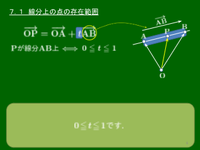
　$\overrightarrow{\mathstrut\rm OP}=\overrightarrow{\mathstrut\rm OA}+t\overrightarrow{\mathstrut\rm AB}$ のとき，

Pが線分AB上 $\iff 0\leqq t\leqq 1$

　よって， \[\begin{align*} &\overrightarrow{\mathstrut p}=\overrightarrow{\mathstrut a}+t(\overrightarrow{\mathstrut b}-\overrightarrow{\mathstrut a})\ \ (0\leqq t\leqq 1)\\[5pt] \iff & \overrightarrow{\mathstrut p}=(1-t)\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut b}\ \ (0\leqq t\leqq 1)\\[5pt] \iff & \overrightarrow{\mathstrut p}=s\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut b}\ \ (s+t=1,0\leqq t\leqq1)\\[5pt] \iff & \overrightarrow{\mathstrut p}=s\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut b}\ \ (s+t=1,s\geqq0,t\geqq0) \end{align*}\]

まとめ\begin{align*} \mbox{点P が線分AB上 }\iff &\overrightarrow{\rm{OP}}=s\overrightarrow{\rm{OA}}+t\overrightarrow{\rm{OB}} \\[5pt] &(s+t=1,\ s\geqq 0,\ t\geqq 0) \end{align*}

7.2　三角形の内部を表すベクトル

　$\overrightarrow{\mathstrut\rm AP}=s\overrightarrow{\mathstrut\rm AB}+t\overrightarrow{\mathstrut\rm AC}$ (ただし，$s+t=k$，$s> 0$，$t> 0$)で表される点Pを考えよう．

\[\overrightarrow{\mathstrut\rm AP}=\frac sk\cdot k\overrightarrow{\mathstrut\rm AB}+\frac tk\cdot k\overrightarrow{\mathstrut\rm AC}\] \[\left(\frac sk+\frac tk=1,\ \frac sk>0,\ \frac tk>0\right)\]

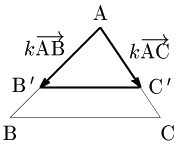
であるから，$k\overrightarrow{\mathstrut\rm AB}=\overrightarrow{\mathstrut\rm AB\,’}$，$k\overrightarrow{\mathstrut\rm AC}=\overrightarrow{\mathstrut\rm AC\,’}$ となる点 $\rm B\,’,\ C\,’$ をとると，Pは線分 $\rm B\,’C\,’$ 上にある．(ただし線分の両端の2点を除く．)
　そこで今，$0 < k < 1$ の範囲で $k$ を動かすと，Pは△ABCの内部にあることがわかる．

例題　△OABにおいて，$\overrightarrow{\rm{OP}}\!=\!s\overrightarrow{\rm{OA}}\!+\!t\overrightarrow{\rm{OB}}\ (s+t\leqq\dfrac12,\ s\geqq 0,\ t\geqq 0)$を満たす点Pは，どのような図形上にあるか．

答

　$0<k\leqq\dfrac12$ なる $k$ を1つ固定し，$s+t=k$，$s\geqq 0$，$t\geqq 0$ で考える．
　$\dfrac sk+\dfrac tk=1$ より，

\[\begin{align*} \overrightarrow{\mathstrut\rm OP}&=s\,\overrightarrow{\mathstrut\rm OA}+t\,\overrightarrow{\mathstrut\rm OB}\\[5pt] &=\frac sk\cdot k\,\overrightarrow{\mathstrut\rm OA}+\frac tk\cdot k\,\overrightarrow{\mathstrut\rm OB}\\[5pt] &=s’\,\overrightarrow{\mathstrut\rm OA\,’}+t’\,\overrightarrow{\mathstrut\rm OB\,’}\\[5pt] &(s’+t’=1,\ s’\geqq 0,\ t’\geqq 0) \end{align*}\]

　ただし，A$’$，B$’$ は $\overrightarrow{\mathstrut\rm OA\,’}=k\,\overrightarrow{\mathstrut\rm OA}$，$\overrightarrow{\mathstrut\rm OB\,’}=k\,\overrightarrow{\mathstrut\rm OB}$ を満たす点である．
　この結果により，Pは線分 $\rm A\,’B\,’$ 上を動くことがわかる．
　ここで，固定していた $k$ を $0 < k\leqq \dfrac12$ で動かし，また $k=0$ のとき，PはOと一致するから，Pの存在領域は，辺OA，OBの中点をそれぞれM，Nとすると，△OMNの周及び内部である．

7.3　2直線の交点を表すベクトル（3つの解法）

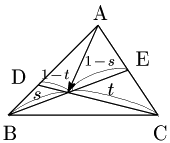
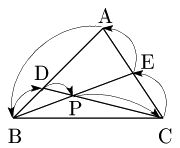
例題　△ABCにおいて，辺ABを $2:1$ に内分する点をD，辺ACの中点をEとし，BE，CDの交点をPとするとき，$\overrightarrow{\rm{AP}}$ を $\overrightarrow{\rm{AB}}$，$\overrightarrow{\rm{AC}}$ で表せ．

答その1

　解法のポイント
　$\overrightarrow{\mathstrut 0}$ でなく，平行でない2つのベクトル $\overrightarrow{\mathstrut a},\overrightarrow{\mathstrut b}$ について， \[\begin{align*} s\overrightarrow{\mathstrut a}+t\overrightarrow{\mathstrut b}&=s’\overrightarrow{\mathstrut a}+t’\overrightarrow{\mathstrut b}\\[5pt] \iff s=s’,\ &\ t=t’ \end{align*}\]

　$\overrightarrow{\mathstrut\rm AP}$ を2通りに表し，係数比較．

\[\overrightarrow{\mathstrut\rm AP}=\left\{\begin{array}{l} (1-s)\overrightarrow{\mathstrut\rm AB}+s\,\overrightarrow{\mathstrut\rm AE}=(1-s)\overrightarrow{\mathstrut\rm AB}+\dfrac s2\overrightarrow{\mathstrut\rm AC}\\[5pt] t\,\overrightarrow{\mathstrut\rm AD}+(1-t)\overrightarrow{\mathstrut\rm AC}=\dfrac23t\,\overrightarrow{\mathstrut\rm AB}+(1-t)\overrightarrow{\mathstrut\rm AC} \end{array}\right.\]

　$\overrightarrow{\mathstrut\rm AB}\neq\overrightarrow{\mathstrut 0}$，$\overrightarrow{\mathstrut\rm AC}\neq\overrightarrow{\mathstrut 0}$，かつ $\overrightarrow{\mathstrut\rm AB}$ と $\overrightarrow{\mathstrut\rm AC}$ は平行ではないから，

\[\left\{ \begin{array}{l} 1-s=\dfrac23t\\[5pt] \dfrac s2=1-t \end{array} \right.\]

　これを解いて，$s=\dfrac12$，$t=\dfrac34$．
　よって，$\underline{\boldsymbol{\dfrac12\overrightarrow{\mathstrut\rm AB}+\dfrac14\overrightarrow{\mathstrut\rm AC}}}$

答その2

　解法のポイント
　Pが線分AB上
　$\iff \overrightarrow{\mathstrut\rm OP}=s\overrightarrow{\mathstrut\rm OA}+t\overrightarrow{\mathstrut\rm OB}\ \ (s+t=1)$

\[\begin{align*} \overrightarrow{\mathstrut\rm AP}&=(1-s)\overrightarrow{\mathstrut\rm AB}+\frac s2\overrightarrow{\mathstrut\rm AC}\\[5pt] &=(1-s)\frac32\overrightarrow{\mathstrut\rm AD}+\frac s2\overrightarrow{\mathstrut\rm AC}\\[5pt] &=\frac32(1-s)\overrightarrow{\mathstrut\rm AD}+\frac s2\overrightarrow{\mathstrut\rm AC} \end{align*}\]

　PはCD上にもあるから，

\[\frac32(1-s)+\frac s2=1\ \ \therefore s=\frac12\]

　よって，$\underline{\boldsymbol{\dfrac12\overrightarrow{\mathstrut\rm AB}+\dfrac14\overrightarrow{\mathstrut\rm AC}}}$

答その3

　解法のポイント
　　メネラウスの定理を利用

　△ADCと直線BEについてメネラウスの定理により，

\[\begin{align*} \frac{\rm AB}{\rm BD}\cdot\frac{\rm DP}{\rm PC}\cdot\frac{\rm CE}{\rm EA}&=1\\[5pt] \therefore \frac31\cdot\frac{\rm DP}{\rm PC}\cdot\frac11&=1\\[5pt] \therefore \frac{\rm DP}{\rm PC}&=\frac13\\[5pt] \therefore {\rm DP}:{\rm PC}&=1:3 \end{align*}\]

　よって，

\[\begin{align*} \overrightarrow{\mathstrut\rm AP}&=\frac{3\overrightarrow{\mathstrut\rm AD}+\overrightarrow{\mathstrut\rm AC}}{1+3}\\[5pt] &=\frac34\overrightarrow{\mathstrut\rm AD}+\frac14\overrightarrow{\mathstrut\rm AC}\\[5pt] &=\underline{\boldsymbol{\frac12\overrightarrow{\mathstrut\rm AB}+\frac14\overrightarrow{\mathstrut\rm AC}}} \end{align*}\]

高校数学ノート[総目次]

数学B　第1章　ベクトル

	スライド	ノート
1. ベクトルと有向線分	[無料]
2. ベクトルの演算	[無料]
3. ベクトルの成分	[無料]
4. ベクトルの内積	[会員]
5. 位置ベクトル	[会員]
6. ベクトル方程式	[会員]
7. 平面ベクトルの応用	[会員]
8. 空間ベクトル	[会員]
9. 空間ベクトルの成分	[会員]
10. 空間ベクトルの内積	[会員]
11. 空間の位置ベクトル	[会員]
12. 空間ベクトルの応用	[会員]
13. 空間のベクトル方程式	[会員]