13. 空間のベクトル方程式(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学B　第1章　ベクトル

	スライド	ノート
1. ベクトルと有向線分	[無料]
2. ベクトルの演算	[無料]
3. ベクトルの成分	[無料]
4. ベクトルの内積	[会員]
5. 位置ベクトル	[会員]
6. ベクトル方程式	[会員]
7. 平面ベクトルの応用	[会員]
8. 空間ベクトル	[会員]
9. 空間ベクトルの成分	[会員]
10. 空間ベクトルの内積	[会員]
11. 空間の位置ベクトル	[会員]
12. 空間ベクトルの応用	[会員]
13. 空間のベクトル方程式	[会員]

13．空間のベクトル方程式

13.1　球面のベクトル方程式

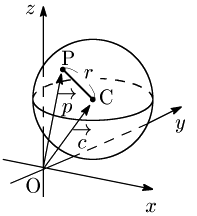
　定点 ${\rm C}(\overrightarrow{\mathstrut c})$ から一定の距離 $r$ にある点の集合は，点 ${\rm C}$ を中心とした半径 $r$ の球となる．球面上の点を ${\rm P}(\overrightarrow{\mathstrut p})$ とすると，

\[|\overrightarrow{{\rm CP}}|=r\]

　よって，

\[ |\overrightarrow{\mathstrut p}-\overrightarrow{\mathstrut c}|=r\]

　これを球面のベクトル方程式という．

　${\rm C}(a,b,c)$，${\rm P}(x,y,z)$ のとき，

\[\begin{align*} |\overrightarrow{\mathstrut p}-\overrightarrow{\mathstrut c}|^2&=|(x-a,y-b,z-c)|^2\\[5pt] &=(x-a)^2+(y-b)^2+(z-c)^2 \end{align*}\]

となるから次が成り立つ：

　点 $(a,\ b,\ c)$ を中心とする半径 $r$ の球面の方程式は\[(x-a)^2+(y-b)^2+(z-c)^2=r^2\]　特に，中心が原点のとき，\[x^2+y^2+z^2=r^2\]

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]

数学B　第1章　ベクトル

	スライド	ノート
1. ベクトルと有向線分	[無料]
2. ベクトルの演算	[無料]
3. ベクトルの成分	[無料]
4. ベクトルの内積	[会員]
5. 位置ベクトル	[会員]
6. ベクトル方程式	[会員]
7. 平面ベクトルの応用	[会員]
8. 空間ベクトル	[会員]
9. 空間ベクトルの成分	[会員]
10. 空間ベクトルの内積	[会員]
11. 空間の位置ベクトル	[会員]
12. 空間ベクトルの応用	[会員]
13. 空間のベクトル方程式	[会員]