3. 2次関数の最大・最小(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅰ　第1章　2次関数

	スライド	ノート	問題
1. 2次関数のグラフ	[無料]		[会員]
2. 関数のグラフの移動	[無料]		[会員]
3. 2次関数の最大・最小	[無料]		[会員]
4. 2次関数の決定	[無料]		[会員]
5. 2次関数のグラフと方程式	[無料]		[会員]
6. 2次不等式とグラフ	[無料]		[会員]
7. 2次方程式の解の配置	[無料]		[会員]

3.　2次関数の最大・最小

2次関数の最大・最小は，それほど複雑ではない

　2次関数は値が大きくなったり小さくなったりする上，グラフが曲線であるため，1次関数より状況はずっと複雑である．しかし最大・最小を考えるというだけなら，問題となるのは軸を挟んで関数の値が減少から増加に転じたり，その逆に増加から減少に転じたりという点だけである．従って今考えている範囲が軸を含まないなら1次関数の最大・最小を考えることとさして変わるところはない．

　例えば2次関数 $y=x^2-4x+5$ を考えよう．平方完成すると $y=(x-2)^2+1$ となるから，頂点の座標は $(2,\ 1)$，軸は直線 $x=2$ である．従ってグラフは次のようになる．

　グラフを見ると

$x\leqq2$ で減少，$x\geqq2$ で増加

していることがわかる．よってこの2次関数は $x=2$ で最小値1をとる．一方， $x$ の値をどんどん小さくしたり，逆にどんどん大きくしていくと， $y$ の値はいくらでも大きくなることもグラフからわかる．従って最大値はない．数学Ⅲになると「$\infty$(正の無限大)」という記号が出てきて，これを知っていると「最大値は $\infty$」といいたくなるかもしれないがこれは正しくない．数学では「$\infty$」は特定の値を指す記号ではないので最大「値」と呼ぶわけにはいかないのである．
　さてここで，定義域を $3\leqq x\leqq 4$ に制限してみよう．この範囲における最大値・最小値はどうなっているであろうか．

　グラフから一目瞭然， $x=3$ で最小値2， $x=4$ で最大値5をとっている．そう判断した私たちの思考を冷静に振り返ってみると，実は1次関数のグラフ，即ち直線を見てどちらがより大きいか小さいかを判断しているときとまるで同じである．途中が曲線だろうが直線だろうが，最大・最小を判断するうえでは問題にならない．グラフが右上がりだということがわかったら，私たちは両端の値しか見ていないのである．

3.1　2次関数の最大・最小

2次関数の最大・最小にはいくつかのパターンがある

　2次関数の最大・最小を考える上で，まず大きく分けて2つの場合がある．一つには定義域に制限がなく実数全体のとき，そしてもう一つには定義域に制限があるときである．後者の場合には更に，軸が含まれるかどうかで場合分けが生じる．

　以下では，2次関数を $y\!=\!ax^2\!+\!bx\!+\!c
\ \ (=f(x)$ とする) とし，これが

\[y=a(x-p)^2+q\]

と変形できたとする．つまりグラフは

　頂点：$(p,\ q)$　　軸：直線 $x=p$

である．

定義域に制限がなく実数全体のとき

　この場合は2次の係数 $a$ が正の場合と負の場合で状況が異なる．

[1]　$\boldsymbol{a>0}$ のとき

　グラフは図のように下に凸であるから，頂点の $y$ 座標が最小値となるが，最大値の方はいくらでも大きくなるので存在しない．

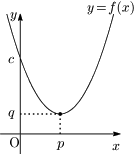
• $x=p$ で最小値 $q$
• 最大値はない

[2]　$\boldsymbol{a<0}$ のとき

　$a>0$ の場合とは逆にグラフは上に凸となるから，頂点の $y$ 座標が最大値となる．一方，最小値の方はいくらでも小さくなるので存在しない．

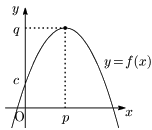
• $x=p$ で最大値 $q$
• 最小値はない

問題１【基本】
　次の2次関数に最大値，最小値があればそれを求めよ．最大値または最小値をとるときの $x$ の値もあわせて求めよ．
(1)　$y=x^2-4x+5$　(2)　$y=-2x^2+4x$

答えは 演習問題 へ

定義域に制限があるとき

　定義域が $x_1\!\leqq\! x\!\leqq\! x_2$ であるとする．このように定義域に制限がかかっているときには，まずもってグラフの軸がその範囲に入っているのかどうかを検討しなければならない．

[1]　軸が定義域に含まれるとき

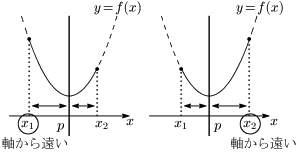
$\boldsymbol{a>0}$ のとき

　グラフは下に凸であるから，頂点の $y$ 座標が最小値となる．一方，最大値の方は，グラフが軸に関して対称であることに注意をすると，軸からより遠い方が大きくなり，そこで最大値をとる．

• $x=x_1$ (or $x=x_2$) で最大値 $f(x_1)$ (or $f(x_2)$ )
• $x=p$ で最小値 $q$

$\boldsymbol{a<0}$ のとき

• $x=p$ で最大値 $q$
• $x=x_1$ (or $x=x_2$) で最小値 $f(x_1)$ (or $f(x_2)$ )

[2]　軸が定義域に含まれない場合

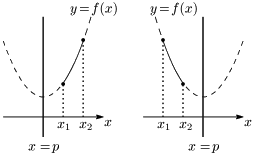
　グラフは曲線ではあるものの，右上がりであるか右下がりであるかのどちらかであるから，1次関数の最大・最小を考察する場合とほぼ同じである．つまり区間の両端で，最大・最小となる．

注意

定義域に制限があるときはいつでも最大・最小があるかといえばそういう訳ではない

　定義域に制限がある場合でも，最大値や最小値がないときもある．

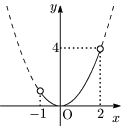
例1　$y=x^2\ (-1<x<2)$

• $x=0$ で最小値0
• 最大値はない．( $y$ は4にいくらでも近い値が取れるが，4自体は取れない．)

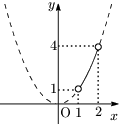
例2　$y=x^2\ (1<x<2)$

最大値も最小値もない

問題２【基本】
　次の2次関数に最大値，最小値があればそれを求めよ．最大値または最小値をとるときの $x$ の値もあわせて求めよ．
(1)　$y=x^2-4x+5$　$(0\leqq x\leqq 1)$
(2)　$y=-2x^2+4x$　$(-1< x\leqq 2)$

答えは 演習問題 へ

3.2　いくつかの例

例題1 [放物線が移動するケース]
2次関数 $y\!=\!x^2\!-\!2ax\ (0\!\leqq\! x\!\leqq\! 2)$ の最小値を求めよ．

　ポイント
　　軸が定義域の内か外で場合分け

答

　$y=x^2-2ax=(x-a)^2-a^2$
　よってグラフは軸が直線 $x=a$ で下に凸．

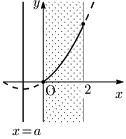
[1]　$a<0$ のとき

　　$x=0$ で最小値0

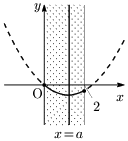
[2]　$0\leqq a\leqq 2$ のとき

　　$x=a$ で最小値 $-a^2$

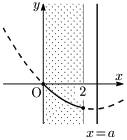
[3]　$a>2$ のとき

　　$x=2$ で最小値 $4-4a$

発展的補足

レベルは高いが入試問題では大いに役立つ最大・最小の考え方

　一般に2次関数で最大・最小となり得るのは

①定義域の左端　②定義域の右端　③頂点の $y$ 座標

の3つであってこれ以外にない．従って本問の場合でも 最小値の候補となるのは，定義域の左端の $x=0$ のときか， 定義域の右端である $x=2$ のときか，頂点である $x=a$ のときかの3つであり，これらの値は順に

\[0,\ \ 4-4a,\ \ -a^2\]

となる．この3つのうちのどれになるかは $a$ の値次第であるから， $y=x^2-2ax\ \ (0\leqq x\leqq 2)$ の最小値を $m(a)$ とすれば，

\[m(a)={\rm min}\{\ 0,\ 4-4a,\ -a^2\ \}\]

と表される．(すぐ下の注参照)

注　${\rm min}\{x,\ y\}$ で，$x$ と $y$ のうち，大きくない方の値を表す．

　ただし，上の3つの候補のうち $-a^2$ だけは，軸が定義域に入っている $0\leqq a\leqq 2$ のときのみ有効であることに注意が必要である．

　$m(a)$ のグラフは，各 $a$ において最小となるグラフをつないでいった，以下の太い実線部分となる：

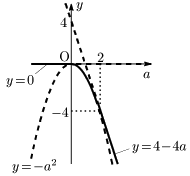
　従って $m(a)$ は次のようになる：

\[m(a)=\left\{ \begin{array}{ll} 0&(a<0)\\[5pt] -a^2&(0\leqq a\leqq2)\\[5pt] 4-4a&(a>2) \end{array}\right.\]

例題2 [定義域が移動するケース]
2次関数 $y\!=\!x^2\!-\!2x\ (a\!\leqq\! x\!\leqq\! a+2)$ の最小値を求めよ．

答

　$y=x^2-2x=(x-1)^2-1$
　よってグラフは軸が直線 $x=1$ で，下に凸である．

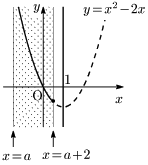
[1]　$a+2<1(\iff a<-1)$ のとき

　　$x=a+2$ で最小値 $a^2+2a$

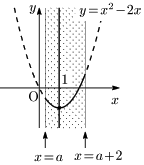
[2]　$a\leqq 1\leqq a+2$ $(\iff -1\leqq a\leqq 1)$ のとき

　　$x=1$ で最小値 $-1$

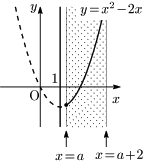
[3]　$a>1$ のとき

　　$x=a$ で最小値 $a^2-2a$

発展的補足

　最小値の候補は，定義域の両端，もしくは頂点の $y$ 座標であるから，

\[a^2+2a,\ \ a^2-2a,\ \ -1\]

の3つである．

　$y=x^2-2x\ (a\leqq x\leqq a+2)$ の最小値を $m(a)$ とすれば，

\[m(a)={\rm min}\{a^2+2a,\ a^2-2a,\ -1\}\]

と表せる．ただし，$-1$ は軸が定義域に入っている $-1\leqq a\leqq 1$ のときのみ有効である．

　$m(a)$ のグラフは，各 $a$ において，最小となるグラフをつないでいった図の太い実線部分となる：

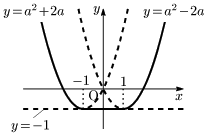
　従って $m(a)$ は次のようになる：

\[m(a)=\left\{ \begin{array}{ll} a^2+2a&(a< -1)\\[5pt] -1&(-1\leqq a\leqq1)\\[5pt] a^2-2a&(a>1) \end{array}\right.\]

このあとは演習問題 で理解を確認！

次は，4．2次関数の決定
前は，2．関数のグラフの移動

---

高校数学[総目次]

数学Ⅰ　第1章　2次関数

	スライド	ノート	問題
1. 2次関数のグラフ	[無料]		[会員]
2. 関数のグラフの移動	[無料]		[会員]
3. 2次関数の最大・最小	[無料]		[会員]
4. 2次関数の決定	[無料]		[会員]
5. 2次関数のグラフと方程式	[無料]		[会員]
6. 2次不等式とグラフ	[無料]		[会員]
7. 2次方程式の解の配置	[無料]		[会員]