高校数学[総目次]
数学Ⅰ 第1章 2次関数
| スライド | ノート | |
| 1. 2次関数のグラフ | [無料] | |
| 2. 関数のグラフの移動 | [無料] | |
| 3. 2次関数の最大・最小 | [無料] | |
| 4. 2次関数の決定 | [無料] | |
| 5. 2次関数のグラフと方程式 | [無料] | |
| 6. 2次不等式とグラフ | [無料] | |
| 7. 2次方程式の解の配置 | [無料] |

1. 2次関数のグラフ
中学校で「$y$ が $x$ の関数で,$y=ax^2(a\neq0)$ の形で表されるとき,$y$ は $x^2$ に比例する」という形で2次関数を学んだ.これによって考察の対象が,これまで例えば「毎分70mで $x$ 分歩くときの距離」とか,「5Lの水が入った水槽に毎分2Lで $x$ 分間水を入れたときの水槽の中の水の量」といった直線的な関係を表すものに限定されてきたものが,「相似比が $1:x$ の2つの三角形の面積比」や「高さ2mのところから自由落下させたときの $t$ 秒後の移動量」といった曲線的な関係を表すものにまで拡張することができた.高校の数学Ⅰではこれをさらに発展させて,一般の2次関数 $y=ax^2+bx+c$ とそのグラフを取り扱う.
2次関数は高等学校のごく初期に学ぶ分野であるが,その内容は他の分野の応用にもたびたび顔を出すほど重要なもので,特に最大値・最小値を考えさせる問題では結局のところ2次関数の理論に帰着させることが多い.もちろん大学入試においても最重要の分野である.
1.1 $y=ax^2$ のグラフ
まずは中学校で習った関数 $y=ax^2$ の復習から始めよう.
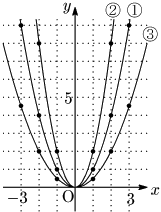
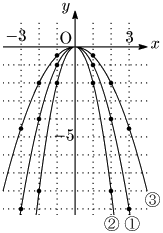
$a>0$ のとき
① $y=x^2$

② $y=2x^2$
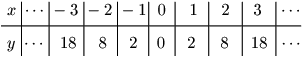
③ $y=\dfrac12x^2$
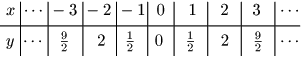
$a<0$ のとき
① $y=-x^2$
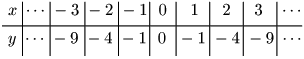
② $y=2x^2$
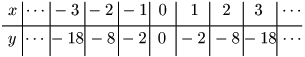
③ $y=-\dfrac12x^2$
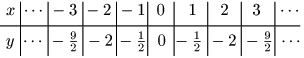

1.2 $y=ax^2+q$ のグラフ
次に,前節で復習した $y=ax^2$ のグラフを $y$ 軸方向に$q$ だけ平行移動したときの式を考えよう.
放物線 $y=ax^2\ \ \cdots$ ①上の任意の点を $(x,y)$ とし,この点を $y$ 軸方向に $q$ だけ平行移動した点を $(X,Y)$ とする:
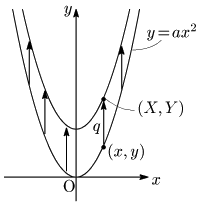
$(x,y)$ と $(X,Y)$ の関係は,
\[\left\{ \begin{array}{l} X=x\\[5pt] Y=y+q \end{array}\right.\ \ \ \therefore \left\{\begin{array}{l} x=X\\[5pt] y=Y-q \end{array}\right.\]
これらを①に代入すると,$X$ と $Y$ の関係式が得られる:
\[Y-q=aX^2\]
\[\therefore Y=aX^2+q\ \ (y=ax^2+q)\]
従って次が成り立つ:
$y=ax^2+q$ のグラフ
2次関数 $y=ax^2+q$ のグラフは,$y=ax^2$ のグラフを $y$ 軸方向に $q$ だけ平行移動したものとなる.

1.3 $y=a(x-p)^2$ のグラフ
続いて,1.1節で復習した $y=ax^2$ のグラフを $x$ 軸方向に$p$ だけ平行移動したときの式を考えよう.
放物線 $y=ax^2\ \ \cdots$ ①上の任意の点を $(x,y)$ とし,この点を $x$ 軸方向に $p$ だけ平行移動した点を $(X,Y)$ とする:
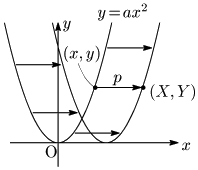
$(x,y)$ と $(X,Y)$ の関係は,
\[\left\{ \begin{array}{l} X=x+p\\[5pt] Y=y \end{array}\right.\ \ \ \therefore \left\{\begin{array}{l} x=X-p\\[5pt] y=Y \end{array}\right.\]
これらを①に代入すると,$X$ と $Y$ の関係式が得られる:
\[Y=a(X-p)^2\ \ (y=a(x-p)^2)\]
従って次が成り立つ:
$y=a(x-p)^2$ のグラフ 2次関数 $y=a(x-p)^2$ のグラフは,$y=ax^2$ のグラフを $x$ 軸方向に $p$ だけ平行移動したものとなる.

1.4 $y\!=\!a(x\!-\!p)^2\!+\!q$ のグラフ
1.2節と1.3節で $y$ 軸方向と $x$ 軸方向の平行移動の式を導いたが,それをミックスしたものがこの節で扱う $y=a(x-p)^2+q$ の形で,これが2次関数の変形の最終形となる.
放物線 $y=ax^2\ \ \cdots$ ①上の任意の点を $(x,y)$ とし,この点を
$x$ 軸方向に $p$,$y$ 軸方向に $q$
だけ平行移動した点を $(X,Y)$ とする:
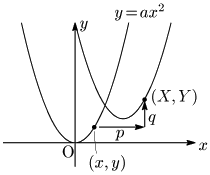
$(x,y)$ と $(X,Y)$ の関係は,
\[\left\{ \begin{array}{l} X=x+p\\[5pt] Y=y+q \end{array}\right.\ \ \ \therefore \left\{\begin{array}{l} x=X-p\\[5pt] y=Y-q \end{array}\right.\]
これらを①に代入すると,$X$ と $Y$ の関係式が得られる:
\[Y-q=a(X-p)^2\]
\[\therefore Y=a(X-p)^2+q\ \ (y=a(x-p)^2+q)\]
従って次が成り立つ:
$y=a(x-p)^2+q$ のグラフ 2次関数 $y=a(x-p)^2+q$ のグラフは,$y=ax^2$ のグラフを\[x\mbox{ 軸方向に }p,\ y\mbox{ 軸方向に }q\]だけ平行移動したものとなる.このとき,\[\mbox{軸:直線 }x=p,\ \mbox{頂点 }(p,q)\]

1.5 $y\!=\!ax^2\!+\!bx\!+\!c$ のグラフ
どのような2次関数も $y=ax^2+bx+c$ で表せるが,この形のままだとグラフをかくことは難しい.1.4節で学んだ $y=a(x-p)^2+q$ の形になってこそ,このグラフの状況を詳しくとらえることができるのである.
ポイント 変形して $\boldsymbol{y=a(x-p)^2+q}$ の形にする.
補足
$ax^2+bx+c$ を $a(x-p)^2+q$ の形に変形することを平方完成するという.
例題 放物線 $y\!=\!-3x^2\!+\!6x\!+\!4$ の軸と頂点の座標を求めよ.
答
解答例を表示する >
次は,2.関数のグラフの移動
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅰ 第1章 2次関数
| スライド | ノート | |
| 1. 2次関数のグラフ | [無料] | |
| 2. 関数のグラフの移動 | [無料] | |
| 3. 2次関数の最大・最小 | [無料] | |
| 4. 2次関数の決定 | [無料] | |
| 5. 2次関数のグラフと方程式 | [無料] | |
| 6. 2次不等式とグラフ | [無料] | |
| 7. 2次方程式の解の配置 | [無料] |

