このページにある内容は，こちらのスライド でわかり易く説明しています．

スライド学習なら驚くほどわかり易い！

PC環境なら全画面表示でより見やすく，よりわかりやすい！
全画面表示の仕方は こちら

高校数学[総目次]

数学Ⅰ　第1章　2次関数

  スライド ノート 問題
1. 2次関数のグラフ [無料]   [会員]
2. 関数のグラフの移動 [無料]   [会員]
3. 2次関数の最大・最小 [無料]   [会員]
4. 2次関数の決定 [無料]   [会員]
5. 2次関数のグラフと方程式 [無料]   [会員]
6. 2次不等式とグラフ [無料]   [会員]
7. 2次方程式の解の配置 [無料]   [会員]

7.　2次方程式の解の配置

7.1　2次方程式の解の配置

方程式の解の配置は目で考えるのが基本

　2次方程式の解について，例えば「2つの解がともに正であるための条件」とか，「一方は正で他方は負であるための条件」といったように，方程式の解の性質について問う問題は，しばしば「方程式の解の配置問題」と呼ばれる．こういった問題を考える上での最良の方策は

解を目で捉える

ことである．

方程式の解を目で捉えるとは一体どういうことか？

　2次関数 $y=x^2-4x+3$ を例にとろう．このグラフの $x$ 切片，すなわち $x$ 軸と交わる点の $x$ 座標は何であろうか？
　$x$ 軸とは $y$ 座標が0である点の集合である．従って関数の $y$ を0とおくと，$0=x^2-4x+3$ 即ち

\[x^2-4x+3=0\]

を $x$ は満たす．これを解くと

\[(x-1)(x-3)=0\ \ \ \ \therefore x=1,\ 3\]

　従って $x$ 切片は1と3であることがわかった．
　グラフは次のようである：

方程式の実数解と $x$ 切片は完全に対応している

　私たちが上の操作でやったことは何だったのだろうか？それは2次関数 $y=x^2-4x+3$ のグラフの $x$ 切片を知るのに

2次方程式 $\boldsymbol{x^2-4x+3=0}$ を解いた

のである．そしてこれは逆に考えることもできて，2次方程式 $x^2-4x+3=0$ の実数解が知りたければ

2次関数 $\boldsymbol{y=x^2-4x+3}$ のグラフの $x$ 切片を見ればよい

のである．このように2次方程式の実数解と2次関数のグラフの $x$ 切片は完全に対応しているのであって，従って2次方程式の実数解の配置を考えるには，2次関数のグラフの $x$ 切片がどうなっているかを考えればよいのである．これが

解を目で捉える

の正体である．例えば両方の解が正であるという条件は，グラフが $x$ 軸の正の部分と2点で交わる条件を求めればよい．このような同値な言いかえによって，視覚的に捉えていくことが肝要である．

7.2　いくつかの例

　以下では2次方程式 $ax^2+bx+c=0$ (ただし $a>0$) の左辺を $f(x)$，判別式を $D$ とする．この2次方程式の2解について，様々な設定下での条件を考えていこう．

[1]　ともに $p$ より大きい

　次の3条件を課せばよい：
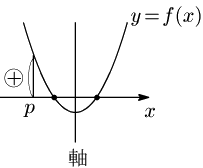
　　　　①　(軸)$>p$
　　　　②　$D\geqq 0$
　　　　③　$f(p)>0$

補足

　上の3条件のどれ1つとして欠けてはならない．実際に次の図からそれを確かめておこう．

①の (軸)$>p$ だけを満たさない


解は共に $p$ 以下

②の $D\geqq 0$ だけを満たさない


実数解をもたない

③の $f(p)>0$ だけを満たさない


$p$ の両側に解がある

[2]　ともに $p$ より大きく $q$ 未満

　次の4条件を課せばよい：
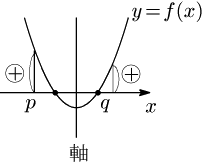
　　　　①　$p<$(軸)$< q$
　　　　②　$D\geqq 0$
　　　　③　$f(p)>0$
　　　　④　$f(q)>0$

[3]　一方が $p$ より大きく，他方が $p$ 未満

　次のたった1つの条件を課せばよい：
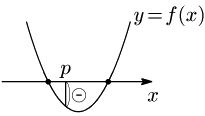
　　　　①　$f(p)< 0$

よくある質問

すぐ上の[3]で $\boldsymbol{D>0}$ の条件は必要ないのですか？

必要ない．

　どうしてかといえば，

\[f(x)\!=ax^2\!+\!bx\!+\!c\!=\!a\left(x\!+\!\frac b{2a}\right)^2\!-\!\frac D{4a}\]

\[(\mbox{ただし，}D=b^2-4ac)\]

であり，$a>0$ に注意すると $f(x)$ の最小値は $-\dfrac D{4a}$ となるが，

\[\begin{align*} f(p)<0 &\Rightarrow f(x)\mbox{の最小値}< 0\\[5pt] &\Rightarrow -\frac D{4a}< 0\\[5pt] &\Rightarrow D>0 \ \ (\because a>0) \end{align*}\]

となり，$f(p)< 0$ から自然に $D>0$ が従うからである．最小値でないところに負の値があるならば，それより小さな値である最小値が負となるのは当然であろう．下に凸な放物線をイメージすれば，どこか1か所でも負になる，すなわち $x$ 軸の下側に潜り込んでいるならば，その放物線は $x$ 軸と異なる2点で交わっているわけで，「＝0」とおいた2次方程式が異なる2つの実数解をもつことは明らかである．

このページで疑問は解決されましたか？

　こちら から数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]

数学Ⅰ　第1章　2次関数

  スライド ノート 問題
1. 2次関数のグラフ [無料]   [会員]
2. 関数のグラフの移動 [無料]   [会員]
3. 2次関数の最大・最小 [無料]   [会員]
4. 2次関数の決定 [無料]   [会員]
5. 2次関数のグラフと方程式 [無料]   [会員]
6. 2次不等式とグラフ [無料]   [会員]
7. 2次方程式の解の配置 [無料]   [会員]