このページにある内容は,こちらのスライドでわかり易く説明しています.
高校数学[総目次]
数学Ⅰ 第1章 2次関数
| スライド | ノート | |
| 1. 2次関数のグラフ | [無料] | |
| 2. 関数のグラフの移動 | [無料] | |
| 3. 2次関数の最大・最小 | [無料] | |
| 4. 2次関数の決定 | [無料] | |
| 5. 2次関数のグラフと方程式 | [無料] | |
| 6. 2次不等式とグラフ | [無料] | |
| 7. 2次方程式の解の配置 | [無料] |

6. 2次不等式とグラフ
6.1 2次不等式
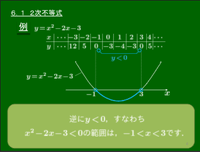
例 $y=x^2-2x-3\,[\,=(x+1)(x-3)\,]$
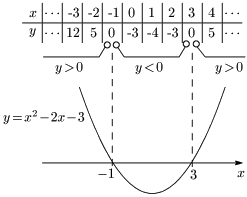
グラフより,
$y>0$ すなわち $x^2-2x-3>0\iff x<-1,\ 3<x$
$y<0$ すなわち $x^2-2x-3<0\iff -1<x<3$
一般に次が成り立つ:
$a\!>\!0$とする.2次方程式 $ax^2\!+\!bx\!+\!c\!=\!0$ が異なる2つの実数解 $\alpha,\beta\ (\alpha<\beta)$ をもつとき,\begin{align*} &ax^2\!+\!bx\!+\!c\!>\!0\mbox{ の解は}\ x\!<\!\alpha,\beta\!<\!x\\[5pt] &ax^2\!+\!bx\!+\!c\!\geqq\!0\mbox{ の解は}\ x\!\leqq\!\alpha,\beta\!\leqq\! x\\[5pt] &ax^2\!+\!bx\!+\!c\!<\!0\mbox{ の解は}\ \alpha\!<\!x\!<\!\beta\\[5pt] &ax^2\!+\!bx\!+\!c\!\leqq\!0\mbox{ の解は}\ \alpha\!\leqq\!x\!\leqq\!\beta \end{align*}
補足
$a <0$ のときは,両辺に $-1$ を掛けて,$x^2$ の係数を正にしてから考えるとよい.
(このとき不等号の向きが変わるので注意.)

6.2 放物線が $x$ 軸に接する場合
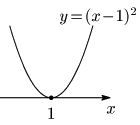
例として,2次関数 $y=x^2-2x+1$ を考えると, $y=x^2-2x+1=(x-1)^2$ により,グラフは $x$ 軸に $x=1$ で接する下に凸な放物線である.よって,
$x^2-2x+1>0$ の解は,$x<1,\ 1<x$
$x^2-2x+1\geqq0$ の解は,すべての実数
$x^2-2x+1<0$ の解は,なし
$x^2-2x+1\leqq0$ の解は,$x=1$ (等式!)
※4番目の例では不等式の解が等式となっていることに注意.
$a\!>\!0$とする.2次方程式 $ax^2\!+\!bx\!+\!c\!=\!0$ が $p$ を重解にもつとき,\begin{align*} &ax^2\!+\!bx\!+\!c\!>\!0\mbox{ の解は}\ x\!<\!p,p\!<\!x\\[5pt] &ax^2\!+\!bx\!+\!c\!\geqq\!0\mbox{ の解は すべての実数}\\[5pt] &ax^2\!+\!bx\!+\!c\!<\!0\mbox{ の解は なし}\\[5pt] &ax^2\!+\!bx\!+\!c\!\leqq\!0\mbox{ の解は}\ x=p\end{align*}

6.3 放物線が $x$ 軸と共有点をもたない場合
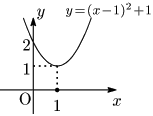
例として,2次関数 $y=x^2-2x+2$ を考えると, $y\!=\!x^2\!-\!2x\!+\!2\!=\!(x\!-\!1)^2\!+\!1$ となるから,グラフは $x$ 軸より上側にある下に凸な放物線である.よって,
$x^2-2x+2>0$ の解は,すべての実数
$x^2-2x+2\geqq0$ の解は,すべての実数
$x^2-2x+2<0$ の解は,なし
$x^2-2x+2\leqq0$ の解は,なし
$a\!>\!0$ とする.2次方程式 $ax^2\!+\!bx\!+\!c\!=\!0$ が 実数解をもたないとき,\begin{align*} &ax^2\!+\!bx\!+\!c\!>\!0\mbox{ の解は すべての実数}\\[5pt] &ax^2\!+\!bx\!+\!c\!\geqq\!0\mbox{ の解は すべての実数}\\[5pt] &ax^2\!+\!bx\!+\!c\!<\!0\mbox{ の解は なし}\\[5pt] &ax^2\!+\!bx\!+\!c\!\leqq\!0\mbox{ の解は なし}\end{align*}
非常によくある間違い
問題 $x^2-2x+2<0$ を解け.
誤答 $x^2-2x+2=0$ を解くと,解の公式から $x=1\pm i$.よって
$1-i<x<1+i\ \ \cdots$ (答)
そもそも虚数に大小の概念はない.($2i<3i$ などは正しくない.) 2次不等式を考える際には常に2次関数のグラフとリンクさせて考えると間違いが少ない.

次は,7.2次方程式の解の配置
前は,5.2次関数のグラフと方程式
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅰ 第1章 2次関数
| スライド | ノート | |
| 1. 2次関数のグラフ | [無料] | |
| 2. 関数のグラフの移動 | [無料] | |
| 3. 2次関数の最大・最小 | [無料] | |
| 4. 2次関数の決定 | [無料] | |
| 5. 2次関数のグラフと方程式 | [無料] | |
| 6. 2次不等式とグラフ | [無料] | |
| 7. 2次方程式の解の配置 | [無料] |
※【ノート】はスライドの内容をまとめたものです.