高校数学[総目次]
数学Ⅰ 第1章 2次関数
| スライド | ノート | 問題 | |
| 1. 2次関数のグラフ | [無料] | [会員] | |
| 2. 関数のグラフの移動 | [無料] | [会員] | |
| 3. 2次関数の最大・最小 | [無料] | [会員] | |
| 4. 2次関数の決定 | [無料] | [会員] | |
| 5. 2次関数のグラフと方程式 | [無料] | [会員] | |
| 6. 2次不等式とグラフ | [無料] | [会員] | |
| 7. 2次方程式の解の配置 | [無料] | [会員] |

5. 2次関数のグラフと方程式
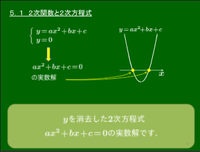
5.1 2次関数と2次方程式
2次関数から2次方程式へ
2次関数 $y=x^2-4x+3$ と $x$ 軸の共有点の個数は何個あるだろうか.グラフで考えてみよう.まず $y$ 切片は3である.また平方完成すると\[y=(x-2)^2-1\]であるから,頂点の座標は $(2,\ -1)$.従ってグラフは次のようになり,$x$ 軸との共有点の個数は2個であることがわかる:
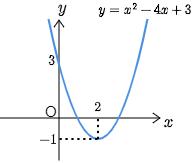
$y=x^2-4x+3$ のグラフ
では次に,$x$ 軸との共有点の $x$ 座標,すなわち $x$ 切片はどうなっているだろうか.$x$ 軸というのは $y$ 座標が0である点の集まりであるから,2次関数 $y=x^2-4x+3$ の $y$ を0とおいた
\[0=x^2-4x+3\]
を考えればよいであろう.因数分解して
\[(x-1)(x-3)=0\ \ \ \therefore x=1,\ 3\]
つまり,$x$ 切片は1と3であることがわかった.
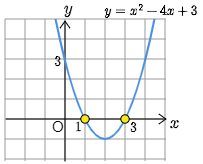
$x$ 軸と1と3で交わる
逆に,今度は2次方程式 $x^2-4x+3=0$ の解について考えることから始めてみよう.方程式の両辺を $y$ とおくと,
\[\left\{\begin{array}{l} y=x^2-4x+3\\[5pt] y=0 \end{array}\right.\]
つまり2次方程式 $x^2-4x+3=0$ の解は,2つの関数 $y=x^2-4x+3$ と $y=0$ のグラフの共有点の $x$ 座標に現れるということがわかる.

一般に,放物線 $y=ax^2+bx+c$ が $x$ 軸 (直線 $y=0$ ) と共有点をもつとき,その $x$ 座標は, \[\left\{\begin{array}{l} y=ax^2+bx+c\\[5pt] y=0 \end{array}\right.\] から $y$ を消去した2次方程式 \[ax^2+bx+c=0\] の実数解である.
逆に2次方程式 $ax^2+bx+c=0$ が実数解をもつとき,この2次方程式の左辺を $y$ とおいた放物線 $y=ax^2+bx+c$ は,右辺を $y$ とおいた直線 $y=0$ ($x$ 軸) と共有点をもつ.
つまり,次が成り立つ:
2次関数 $y\!=\!ax^2\!+\!bx\!+\!c$ のグラフと $x$ 軸との共有点の $x$ 座標は,2次方程式 $\boldsymbol{ax^2\!+\!bx\!+\!c\!=\!0}$ の実数解と等しい.
放物線 $y=ax^2+bx+c$ が $x$ 軸と接する場合や,共有点をもたない場合も,それぞれ次のようになる:
接する $\iff ax^2\!+\!bx\!+\!c\!=\!0$ は重解をもつ
共有点をもたない$\iff ax^2\!+\!bx\!+\!c\!=\!0$ は実数解をもたない
2次関数のグラフと $x$ 軸との関係は,2次方程式の実数解の議論に持ち込む
2次方程式 $ax^2+bx+c=0$ が実数解をもつかどうかは判別式 $D=b^2-4ac$ によって分かるから,まとめると次のようになる:
2次関数 $y\!=\!ax^2\!+\!bx\!+\!c$ のグラフと $x$ 軸との関係は,2次方程式 $ax^2+bx+c=0$ の判別式を $D$ とすると,\begin{align*}&D>0\iff\mbox{異なる2点で交わる}\\ &D=0\iff\mbox{接する}\\ &D<0\iff\mbox{共有点をもたない}\end{align*}
「2次関数の議論から2次方程式の議論へ」またはその逆の「2次方程式の議論から2次関数の議論へ」といった相互の乗り入れが自由にできるようにしておくことが重要である.
例題 2次関数 $y=2x^2+4x+m$ のグラフと $x$ 軸の共有点の個数を求めよ.
答
解答例を表示する
5.2 2次関数のグラフと直線
相手が $x$ 軸ではない一般の直線でも考え方は何一つとして変わらない
放物線 $y=ax^2+bx+c$ と直線 $y=px+q$ から $y$ を消去した
\[ax^2+bx+c=px+q\]
即ち2次方程式
\[ax^2+(b-p)x+c-q=0\]
について,
異なる2つの実数解をもつ $\iff$ 2点で交わる
重解をもつ $\iff$ 接する
実数解をもたない $\iff$ 共有点をもたない
がいえるから,次が成り立つ:
2次関数 $y\!=\!ax^2\!+\!bx\!+\!c$ のグラフと 直線 $y\!=\!px\!+\!q$ の関係は,2次方程式 $ax^2\!+\!(b\!-\!p)x\!+\!c\!-\!q\!=\!0$ の判別式を $D$ とすると,\begin{align*}&D>0\iff\mbox{異なる2点で交わる}\\ &D=0\iff\mbox{接する}\\ &D<0\iff\mbox{共有点をもたない}\end{align*}
例題 2次関数 $y=2x^2+5x$ のグラフと直線 $y=x-m$ との共有点の個数を求めよ.
答
解答例を表示する
5.3 2つの2次関数のグラフ
相手が2次関数,すなわち2次関数どうしの関係でも考え方は基本的に同じ
異なる2つの放物線 $y=ax^2+bx+c$,$y=a’x^2+b’x+c’$ から $y$ を消去した \[ax^2+bx+c=a’x^2+b’x+c’\] 即ち方程式 \[(a-a’)x^2+(b-b’)x+c-c’=0\ \ \cdots\mbox{①}\] について,
$a\neq a’$ のとき
異なる2つの実数解をもつ $\iff$ 2点で交わる
重解をもつ $\iff$ 接する
実数解をもたない $\iff$ 共有点をもたない
従って次が成り立つ:
$a\neq a’$ である2つの2次関数 $y\!=\!ax^2\!+\!bx\!+\!c$ と $y=a’x^2+b’x+c’$ の関係は,2次方程式 $(a-a’)x^2+(b-b’)x+c-c’=0$ の判別式を $D$ とすると,\begin{align*}&D>0\iff\mbox{異なる2点で交わる}\\ &D=0\iff\mbox{接する}\\ &D<0\iff\mbox{共有点をもたない}\end{align*}
$a=a’$ のとき
①は $(b-b’)x+c-c’=0$ となり,$b\neq b’$ ならば1次関数となるから共有点は1つ.
$b=b’$ ならば,共有点はない.
このあとは演習問題 で理解を確認!

次は,6.2次不等式とグラフ
前は,4.2次関数の決定
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅰ 第1章 2次関数
| スライド | ノート | 問題 | |
| 1. 2次関数のグラフ | [無料] | [会員] | |
| 2. 関数のグラフの移動 | [無料] | [会員] | |
| 3. 2次関数の最大・最小 | [無料] | [会員] | |
| 4. 2次関数の決定 | [無料] | [会員] | |
| 5. 2次関数のグラフと方程式 | [無料] | [会員] | |
| 6. 2次不等式とグラフ | [無料] | [会員] | |
| 7. 2次方程式の解の配置 | [無料] | [会員] |
※【ノート】はスライドの内容をまとめたものです.