高校数学[総目次]
数学Ⅰ 第1章 2次関数
| スライド | ノート | 問題 | |
| 1. 2次関数のグラフ | [無料] | [会員] | |
| 2. 関数のグラフの移動 | [無料] | [会員] | |
| 3. 2次関数の最大・最小 | [無料] | [会員] | |
| 4. 2次関数の決定 | [無料] | [会員] | |
| 5. 2次関数のグラフと方程式 | [無料] | [会員] | |
| 6. 2次不等式とグラフ | [無料] | [会員] | |
| 7. 2次方程式の解の配置 | [無料] | [会員] |

2. 2次関数のグラフの移動
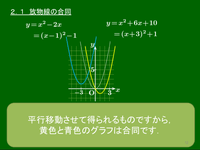
2.1 放物線の合同
$y=ax^2+\mbox{□}\, x+\triangle$ のグラフはもれなく合同である
2つの2次関数 $y=x^2-2x$ と $y=x^2+6x+10$ のグラフの関係について調べる.
$y=x^2-2x=(x-1)^2-1$
→ 放物線 $y=x^2$ を
$x$ 軸方向に1,$y$ 軸方向に $-1$
だけ平行移動したもの.
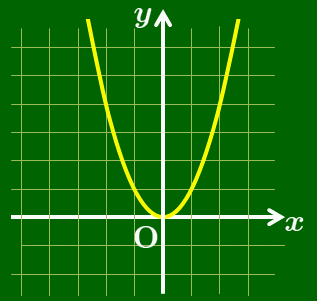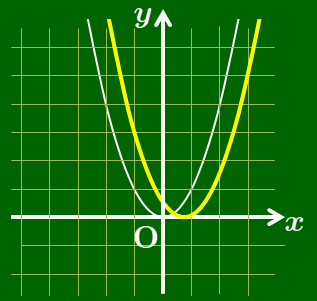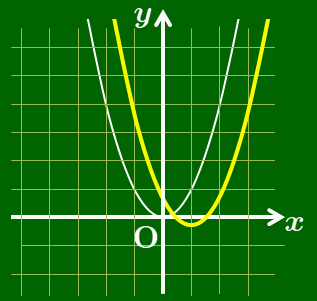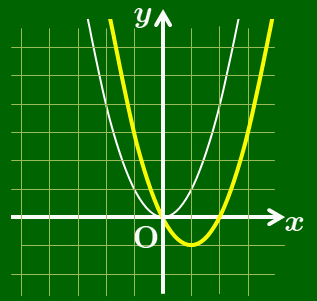
$y=x^2-2x$ のグラフ
$y=x^2+6x+10=(x+3)^2+1$
→ 放物線 $y=x^2$ を
$x$ 軸方向に $-3$,$y$ 軸方向に1
だけ平行移動したもの.
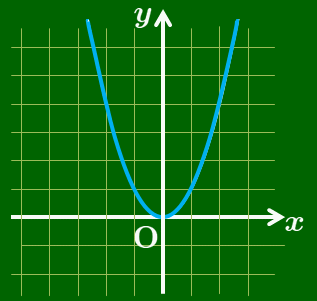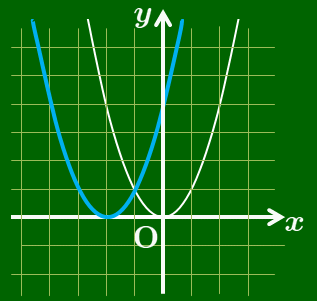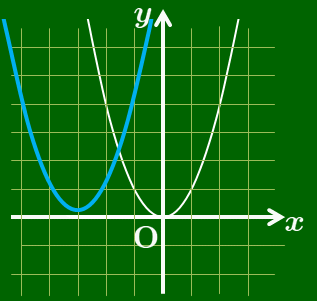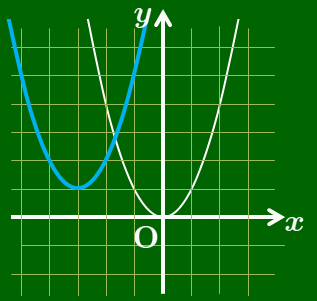
$y=x^2+6x+10$ のグラフ
このように,2つの放物線はいずれも放物線 $y=x^2$ を平行移動させただけだから,この2つの放物線は合同な図形である.
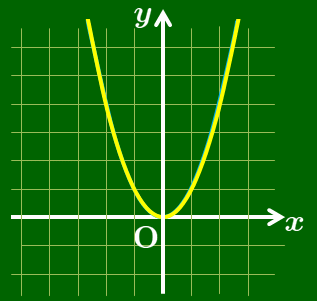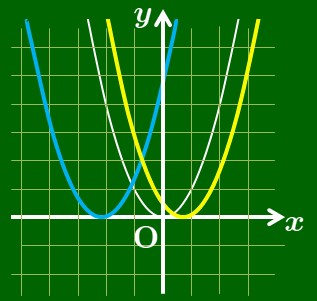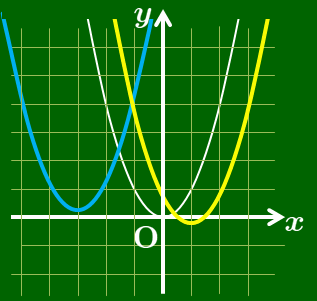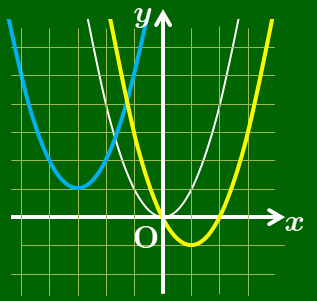
どちらのグラフも $y=ax^2$ のグラフと合同
一般に,放物線 $y=ax^2+bx+c$ はすべて放物線 $y=ax^2$ と合同である.
また,$x^2$ の係数が $-a$ の放物線も,凸性は異なるものの,放物線 $y=ax^2$ と合同である.
重要 放物線 $\boldsymbol{y=ax^2+bx+c}$ の形を決定付けるのは,
2次の係数 $\boldsymbol a$ である
発展的補足
放物線は合同とは限らないが、すべて相似である
すぐ上にある「重要」は,「2次の係数(の絶対値)が等しい2次関数は,グラフがどれも合同である」ということを述べている.では2次の係数(の絶対値)が異なっていたら? もちろんグラフは合同ではない.がしかし実は相似ではある.つまり
2次関数のグラフはすべて相似である
がいえる.下の図の放物線は,平べったいものから細く尖ったものまであって一見すると相似に見えないが,どれも相似である.例えば,右側の細い放物線の頂点辺りをどんどん拡大していくと,いずれ左側の放物線の形が現れる.
証明は数学Ⅱの軌跡 が学習済みなら易しい.2次関数 $y=ax^2$ のグラフを原点を中心として $a$ 倍の相似拡大(縮小)をすると,$y=x^2$ のグラフが得られる.


例題 放物線 $y=2x^2-4x$ を $x$ 軸方向に $-2$,$y$ 軸方向に 5 だけ平行移動させた放物線の方程式を求めよ.
解法1
頂点の移動を捕捉するやり方
平方完成をすると $y=2x^2-4x=2(x-1)^2-2$
従って頂点は,点 $(1,-2)$
頂点を $x$ 軸方向に $-2$,$y$ 軸方向に 5 だけ移動させると,点$(-1,3)$.
2次の係数が2であることに注意して,求める放物線の方程式は, \[\underline{\boldsymbol{y=2(x+1)^2+3}}\ \ \ (y=2x^2+4x+5)\]
解法2
グラフを移動させる公式を使うやり方
放物線 $y=2x^2-4x$ 上の任意の点 $(x,y)$ を $x$ 軸方向に $-2$,$y$ 軸方向に $5$ だけ移動した点を $(X,Y)$ とすると,
\[\left\{\begin{array}{l} X=x-2\\[5pt] Y=y+5 \end{array}\right.\]
小文字 $x,\ y$ について解くと
\[\left\{\begin{array}{l} x=X+2\\[5pt] y=Y-5 \end{array}\right. \]
$x,\ y$ は $y=2x^2-4x$ を満たすから代入して, \[Y-5=2(X+2)^2-4(X+2)\]
展開して整理すると
\[\begin{align*} Y&=2(X+2)^2-4(X+2)+5\\[5pt] &=2(X^2+4X+4)-4X-8+5\\[5pt] &=2X^2+4X+5 \end{align*}\]
これは点 $(X,\ Y)$ が放物線 $y=2x^2+4x+5$ 上にあることを意味する.従って求める方程式は
\[\underline{\boldsymbol{y=2x^2+4x+5}}\]
補足【解法2について,より詳しく】
$y=f(x)$ のグラフを $x$ 軸方向に $p$, $y$ 軸方向に $q$ だけ平行移動するには $x$ を $x-p$,$y$ を $y-q$ に書き換えればよい
解法2でみたようなやり方は,2次関数のグラフの移動に限らず,一般のどんな関数のグラフにも通用する汎用性がある.以下この点について詳しく説明する.
曲線 $y=f(x)\ (\ \cdots$①) 上の任意の点 $(x,y)$ を
$x$ 軸方向に $p$,$y$ 軸方向に $q$
だけ移動した点を $(X,Y)$ とすると,
\[\left\{\begin{array}{l}
X=x+p\\[5pt]
Y=y+q \end{array}\right.\ \ \cdots\mbox{(あ)}
\]
これを小文字 $x,\ y$ について解くと,
\[\left\{\begin{array}{l} x=X-p\\[5pt] y=Y-q \end{array}\right.\ \ \cdots\mbox{(い)}\]
小文字 $x,\ y$ は①を満たすから代入して, \[Y-q=f(X-p)\] これは点 $(X,\ Y)$ が曲線 $y-q=f(x-p)$ 上にあることを意味する.従って次が成り立つ:
グラフの平行移動【公式】 曲線 $y=f(x)$ を $x$ 軸方向に $p$,$y$ 軸方向に $q$ だけ平行移動したグラフの方程式は\[ y-q=f(x-p)\]
繰り返しになるが,この公式は2次関数に限らず,あらゆるグラフの平行移動で有効である.

2.2 直線 $x=p$ に関する対称移動
例題 放物線 $y=x^2-2x$ を直線 $x=2$ に関して対称移動させた放物線の方程式を求めよ.
解法1
頂点の移動を捕捉するやり方
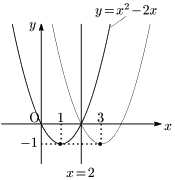
平方完成すると $y=x^2-2x=(x-1)^2-1$
よって頂点の座標は$(1,-1)$.これを直線 $x=2$ に関して対称移動した点の座標は $(3,-1)$ であり,この移動で放物線の凸性は変化しないから,求める放物線の方程式は
$y=(x-3)^2-1\ \ \cdots$ (答)
$(y=x^2-6x+8)$
解法2
軌跡(数学Ⅱ)の考え方によるやり方
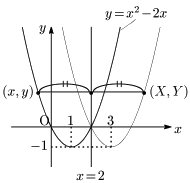
放物線 $y=x^2-2x$ 上の任意の点 $(x,y)$ を,直線 $x=2$ に関して対称移動した点を $(X,Y)$ とすると,
\[ \left\{\begin{array}{l} \dfrac{x+X}2=2\\[5pt] Y=y \end{array}\right. \ \ \ \therefore \left\{\begin{array}{l} x=4-X\\[5pt] y=Y \end{array}\right.\]
これを $y=x^2-2x$ に代入して,
\[\begin{align*} Y&=(4-X)^2-2(4-X)\\[5pt] &=X^2-6X+8 \end{align*}\]
よって求める放物線の方程式は,
$y=x^2-6x+8\ \ \cdots$ (答)

$y$ 軸に関する対称移動
直線 $x=p$ に関する対称移動の特別な場合として,直線 $x=0$ すなわち $y$ 軸に関する対称移動を考えよう.曲線 $y=f(x)$ 上の任意の点 $(x,\ y)$ を $y$ 軸に関して対称移動した点を $(X,\ Y)$ とすると,
\[ \left\{\begin{array}{l} X=-x\\[5pt] Y=y \end{array}\right. \ \ \ \therefore \left\{\begin{array}{l} x=-X\\[5pt] y=Y \end{array}\right.\]
これらを $y=f(x)$ に代入して\[Y=f(-X)\] これは点 $(X,\ Y)$ が曲線 $y=f(-x)$ 上にあることを意味する.つまり,曲線を $y$ 軸に関して対称移動したグラフの方程式は,元の式の $x$ を $-x$ と書き換えればよい.
$y$ 軸に関する対称移動 曲線 $y=f(x)$ を $y$ 軸に関して対称移動した方程式は,\[y=f(-x)\]

2.3 直線 $y=q$ に関する対称移動
例題 放物線 $y=x^2-2x$ を $x$ 軸(直線 $y=0$) に関して対称移動させた放物線の方程式を求めよ.
解法1
頂点の移動を捕捉するやり方
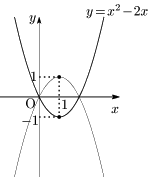
頂点 $(1,-1)$ を $x$ 軸に関して対称移動させると $(1,1)$.
この移動で,グラフが下に凸から上に凸に変わることに注意して,求める放物線の方程式は,
$y=-(x-1)^2+1\ \ \cdots$(答)
$(y=-x^2+2x)$
解法2
軌跡(数学Ⅱ)の考え方によるやり方
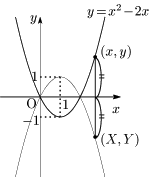
放物線 $y=x^2-2x\ \ \cdots$ ① 上の任意の点 $(x,y)$ を,$x$ 軸に関して対称移動した点を $(X,Y)$ とすると,
\[ \left\{\begin{array}{l} X=x\\[5pt] \dfrac{y+Y}2=0 \end{array}\right. \ \ \ \therefore \left\{\begin{array}{l} x=X\\[5pt] y=-Y \end{array}\right.\]
これを①に代入して,
\[-Y=X^2-2X\]
よって求める放物線の方程式は,
$y=-x^2+2x\ \ \cdots$(答)

$x$ 軸に関する対称移動
直線 $y=q$ に関する対称移動の特別な場合として,直線 $y=0$ すなわち $x$ 軸に関する対称移動を考えよう.曲線 $y=f(x)$ 上の任意の点 $(x,\ y)$ を $x$ 軸に関して対称移動した点を $(X,\ Y)$ とすると,
\[ \left\{\begin{array}{l} X=x\\[5pt] Y=-y \end{array}\right. \ \ \ \therefore \left\{\begin{array}{l} x=X\\[5pt] y=-Y \end{array}\right.\]
これらを $y=f(x)$ に代入して\[-Y=f(X)\ \ \ \therefore Y=-f(X)\] これは点 $(X,\ Y)$ が曲線 $y=-f(x)$ 上にあることを意味する.つまり,曲線を $x$ 軸に関して対称移動したグラフの方程式は,元の式の $y$ を $-y$ と書き換えればよい.
$x$ 軸に関する対称移動 曲線 $y=f(x)$ を $x$ 軸に関して対称移動した方程式は,\[y=-f(x)\]

2.4 原点に関する対称移動
例題 放物線 $y=x^2-2x$ を原点に関して対称移動させた放物線の方程式を求めよ.
解法1
頂点の移動を捕捉するやり方
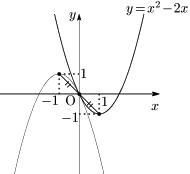
頂点 $(1,-1)$ を 原点に関して対称移動させると $(-1,1)$.
この移動で,グラフが下に凸から上に凸に変わることに注意して,求める放物線の方程式は,
$y=-(x+1)^2+1\ \ \cdots$(答)
$(y=-x^2-2x)$
解法2
軌跡(数学Ⅱ)の考え方によるやり方
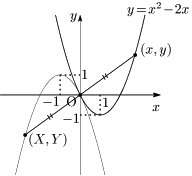
放物線 $y=x^2-2x\ \ \cdots$ ① 上の任意の点 $(x,y)$ を,原点に関して対称移動した点を $(X,Y)$ とすると,
\[ \left\{\begin{array}{l} \dfrac{x+X}2=0\\[5pt] \dfrac{y+Y}2=0 \end{array}\right. \ \ \ \therefore \left\{\begin{array}{l} x=-X\\[5pt] y=-Y \end{array}\right.\]
これを①に代入して,
\[-Y=(-X)^2-2\cdot(-X)\]
よって求める放物線の方程式は,
$y=-x^2-2x\ \ \cdots$(答)

解法2の計算過程からわかるように,曲線 $y=f(x)$ を原点に関して対称移動したグラフの方程式は,$x$ を $-x$ に, $y$ を $-y$ と書き換えればよい.これは $y$ 軸に関する対称移動でやった操作と,$x$ 軸に関する対称移動でやった操作を共に実行することになっている.即ち原点に関する対称移動というのは,$x$ 軸に関する対称移動と$y$ 軸に関する対称移動の両方を実行することでも得られることがわかる.
これまでの対称移動をまとめておこう
曲線の対称移動 曲線$y=f(x)$ の対称移動
$y$ 軸に関して → $y=f(-x)$
$x$ 軸に関して → $y=-f(x)$
原点に関して → $y=-f(-x)$
このあとは演習問題 で理解を確認!

次は,3.2次関数の最大・最小
前は,1.2次関数のグラフ
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅰ 第1章 2次関数
| スライド | ノート | 問題 | |
| 1. 2次関数のグラフ | [無料] | [会員] | |
| 2. 関数のグラフの移動 | [無料] | [会員] | |
| 3. 2次関数の最大・最小 | [無料] | [会員] | |
| 4. 2次関数の決定 | [無料] | [会員] | |
| 5. 2次関数のグラフと方程式 | [無料] | [会員] | |
| 6. 2次不等式とグラフ | [無料] | [会員] | |
| 7. 2次方程式の解の配置 | [無料] | [会員] |